AC快乐机——最最通俗易懂的AC自动机讲解!
AC快乐机
众所周知,KMP是算法竞赛中常用的字符串匹配算法,该算法通过对模式串构建next数组的方式,十分有效的提高了匹配的效率。
单一模式串的匹配可以构造next,那如果模式串有多个,也同样能通过构造next的方式匹配吗?
Fail指针
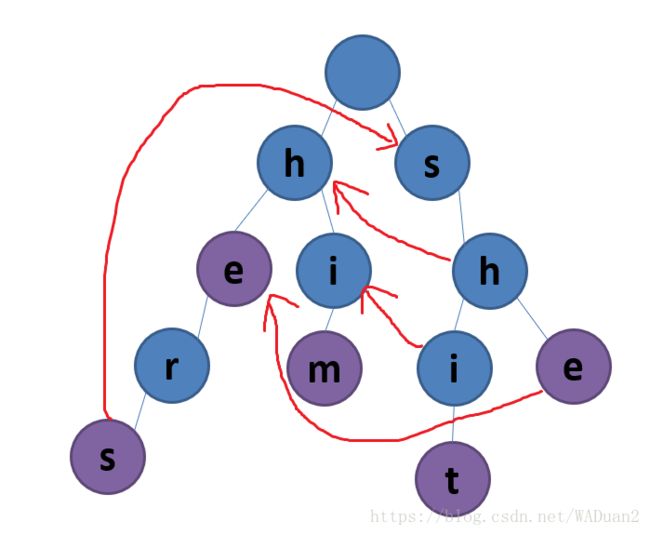
给你多个模式串,也就是给你一棵Trie,在Trie上进行匹配。假设我们有能力构建出一棵Trie的next,考虑KMP中的next的定义(指向最长的后缀),那么一棵Trie的next是长这样的(以模式串he,she,him,hers,shit为例):
这棵Trie的next是这样的(没画的都指向根):
现在要拿主串ashers上去匹配,匹配的方式和KMP一样:如果可以接着向下走则向下走,否则爬next
那么匹配的路径为root-root-s-h-e-e-r-s,最终匹配成功
匹配的复杂度显然是 O ( n + m i n ( n , m ) ) O(n+min(n,m)) O(n+min(n,m))的(其中 n n n为主串长度, m m m为最长的模式串长度)
如果在Trie树上能构造出next的话,匹配复杂度就会变成线性,这就是AC自动机基础的原理啦,AC自动机中next的名字叫做Fail指针(也称后缀节点),接下来的所有next都会用Fail代替
Fail指针是从一个Trie节点(对应字符串 α \alpha α)到另一个Trie节点(对应的字符串 ω \omega ω是 α \alpha α的最长后缀)的有向边
匹配时,如果我们到达了不能继续匹配的节点,我们沿着Fail指针爬以维持尽可能更大的前缀
对于Trie树上每一个节点,我们都可以构造一个Fail指针
Fail指针的构造?
Fail指针的些许小性质:
1.根的所有儿子的Fail都是根
2.节点x的Fail指向y(非根),那么x的t儿子的Fail指向y的t儿子的Fail
以上图为例,she中h的Fail指向的是he中的h,那么sh的e儿子she的Fail就会指h的e儿子he
3.一个节点一直沿着Fail爬会爬到根,期间深度是不断减小的
这样我们有了一个构建Fail的大体思路,对于每一个点,对他所有的儿子构建Fail,然后bfs下去,对t儿子构建Fail的过程可以通过不断爬Fail找到第一个有t儿子的点这一途径得到
但也会有一些不美妙的情况使这个过程变得很不美观
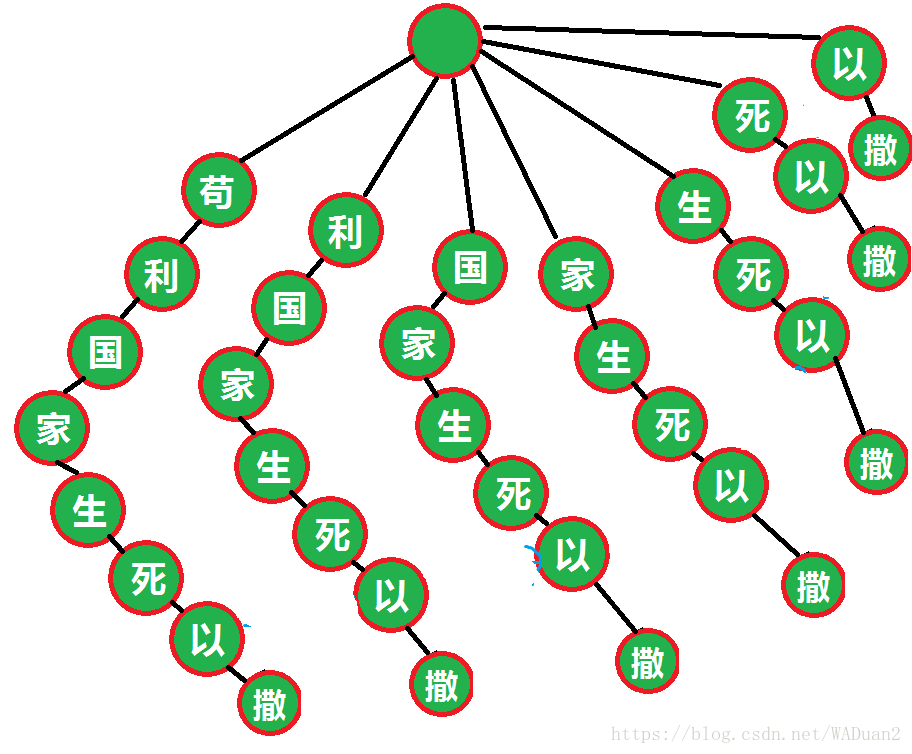
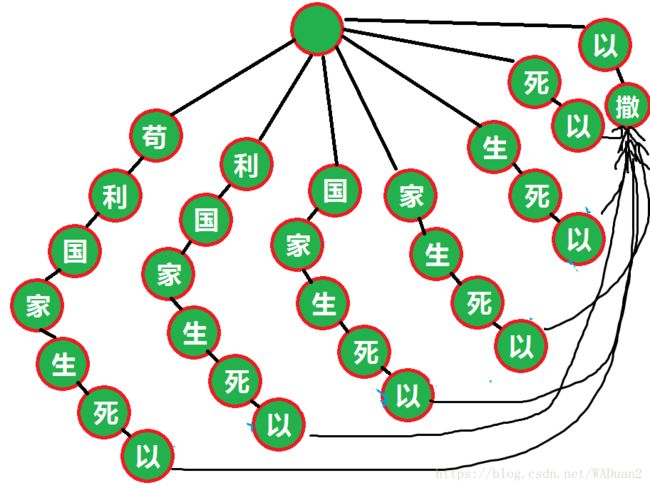
假设上图苟利国家生死以的以有一个撒儿子,用刚才所说的方法构造撒的Fail指针就需要沿着蓝色箭头爬好远好远好远好远好远好远才能找到,这个过程会让过程及复杂度极其不优美,AC自动机用Trie图简化了这个过程
Trie图
(为了方便,将根所有不存在的儿子都设为根)
对于Trie树上的每一个节点 x x x,它的 α \alpha α边指向的是它下一个字符 t t t,表示如果当前状态是 x x x,待匹配字符是 α \alpha α,那么匹配到的点是 t t t
设字符集为 S S S,点 x x x可匹配的(向外延伸出去的)字符集 S ′ ⊆ S S'\subseteq S S′⊆S,即 ∀ α ∈ S ′ \forall \alpha \in S' ∀α∈S′,都可以 x x x(不通过爬Fail的方式)由向外延伸(到 p p p)
此过程描述为:当 x x x的下一个字符是 α \alpha α( α ∈ S ′ \alpha \in S' α∈S′)时,走到的节点是 p p p
但是如果当前状态是 x x x,下一个字符 β ∉ S ′ \beta \notin S' β∈/S′,也就代表着在此失配,那么根据刚才所描述的方法,AC自动机需要爬Fail找到第一个有 β \beta β儿子的点 y y y继续匹配(到 q q q)。
此过程可以描述为:当 x x x的下一个字符是 β \beta β( β ∉ S ′ \beta \notin S' β∈/S′)时,走到的节点是 q q q
这两个过程描述起来十分相似,那么我们为什么不将 q q q直接看作 x x x的 β \beta β儿子呢?
对于节点 x x x,如果它并没有 β \beta β儿子,那么沿着找到第一个有 β \beta β儿子的节点 y y y,并把 y y y的 β \beta β儿子看作是自己的 β \beta β儿子
我们把这个操作称为NTR,NTR过后的图叫Trie图
上图理论上的Trie图是长这样的
但实际上是这样的
如果 x x xNTR了 y y y的 α \alpha α, y y yNTR了 z z z的 α \alpha α,可以直接看作 x x xNTR了 z z z的 α \alpha α,也就是说如果我们按照Fail的顺序构建,NTR操作只要考虑一个Fail就可以了
在Trie图上的匹配只要无脑向后走就可以了,也就是说,构建完Trie图,Fail就没什么用了
Trie图本质上是个有向图
Fail指针 Trie图的构造!
struct Node{
Node *ch[26],*fail;
bool b;
Node():fail(NULL){
b=false;
for(int i=0;i<26;i++)
ch[i]=NULL;
}
}*root=new Node;
queue<Node*>q;
inline void Insert(char *s){///构建Trie
Node *x=root;
int len=strlen(s+1);
for(int i=1;i<=len;i++){
if(!x->ch[s[i]-'0']) x->ch[s[i]-'0']=new Node;
x=x->ch[s[i]-'0'];
}
x->b=true;
}
inline void GetFail(){///AC自动机可以以bfs的方式构建
root->fail=root;///根的Fail是他自己
for(int i=0;i<26;i++){
if(root->ch[i]) q.push(root->ch[i]),root->ch[i]->fail=root;
///将根儿子的Fail指向根,并放入队列里
else root->ch[i]=root;
///如果root没有i这个儿子,就把他的儿子赋为自己,这样以上的性质2对根也满足了
}
while(!q.empty()){
Node *x=q.front();q.pop();
for(int i=0;i<26;i++){
if(x->ch[i]) x->ch[i]->fail=x->fail->ch[i],q.push(x->ch[i]);
///根据性质2搞出各个儿子的Fail
else x->ch[i]=x->fail->ch[i];///NTR操作(
}
Node *tmp=x->fail;
while(tmp!=root && !tmp->b) tmp=tmp->fail;
if(tmp->b) x->b=true;
///如果它的某一后缀是一个模式串,那么它也肯定包含模式串(一些特定的题统计时会用到)
}
}
在Trie图上的匹配过程可以直接当成Trie树上匹配,代码也是一样的
inline int Match(char *c){
int len=strlen(c+1);
int ans=0;
Node *x=root;
for(int i=1;i<=len;i++){
int k=c[i]-'a';
x=x->ch[k];///一直往下走就行了
Node *tmp=x;///这部分是统计的...
while(tmp!=root && !tmp->b){
ans+=tmp->num,tmp->b=true;
tmp=tmp->nex;
}
}
return ans;
}
Fail树
把所有Fail指针当作一条无向边,可以发现构成的是一个树形结构
小例题:
给定一个n个单词的文章,求每个单词在文章中的出现次数 ( n ≤ 200 n\le200 n≤200,单词总长 ≤ 1 0 6 \le 10^6 ≤106)
大体思路:先将所有的串建一个AC自动机,构建的Fail时候到一个点就将所有它的所有Fail都加上1
显然会T
可以发现,一个点一定是它Fail树中子树点的后缀(如果串s能匹配到这里,s就会是子树所有点的后缀)
那么一个串的出现次数事实上就是它Fail树子树中单词数量的和
然后没了