洛谷 P2820 局域网 kruskal与prim算法讲解

题目背景

某个局域网内有n(n<=100)台计算机，由于搭建局域网时工作人员的疏忽，现在局域网内的连接形成了回路，我们知道如果局域网形成回路那么数据将不停的在回路内传输，造成网络卡的现象。因为连接计算机的网线本身不同，所以有一些连线不是很畅通，我们用f(i,j)表示i,j之间连接的畅通程度，f(i,j)值越小表示i,j之间连接越通畅，f(i,j)为0表示i,j之间无网线连接。

题目描述

需要解决回路问题，我们将除去一些连线，使得网络中没有回路，并且被除去网线的Σf(i,j)最大，请求出这个最大值。

输入格式

第一行两个正整数n k。
接下来的k行每行三个正整数i j m表示i,j两台计算机之间有网线联通，通畅程度为m。

输出格式

一个正整数，Σf(i,j)的最大值

输入输出样例

输入

5 5
1 2 8
1 3 1
1 5 3
2 4 5
3 4 2

输出

8

说明/提示

f(i,j)<=1000

题目分析

由该题描述可知在该题背景中计算机的关系形成了一张图，且图中每一条边均有一个权值，而求去除的总共的最大值，也就是说明要保留一条权值和最小的路径也就是最小生成树，故此是一道求最小生成树的题目，对于最小生成树，在图论中我们有kruskal与prim两种算法。

方法一

kruskal算法
对于kruskal算法这里做一个简单的讲解
kruskal算法的核心选取当前最小边同时使用并查集对点进行划分，然后当所有的点进入集合后结束，此时便得到一条最短路径。

如下图，我们首选选择最短的边 即1—— >3这一条边的权值为2，

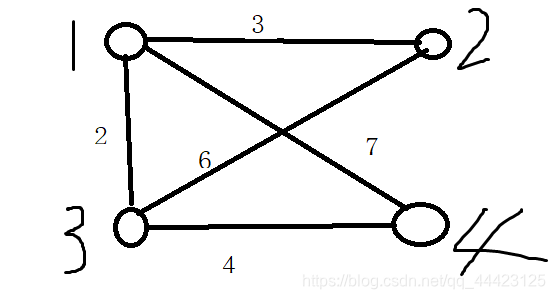
此时我们最短路径加上2，然后使3的点指向1这个点，形成一个集合
此时集合内有1与3这两个点。

然后我们继续寻找下一个未选取的边中的最小边。即1——>2这一条边，该边权值为3故最短进加上3，此时最短路径长度为5.
同样重复上面的步骤，由于2这个点未处于集合中将2指向1

然后我们继续寻找下一个未选取的边中的最小边。即3——>4这一条边，该边权值为4故最短进加上4，此时最短路径长度为9.
同样重复上面的步骤，由于4这个点未处于集合中将4指向3

此时所有的点已经全部处于集合当中。最短路径查找完成

其路径为下图

首先我们可以定义一个结构体存储每一条边并存储每条边的左右端点同时加上每条边的权值得到所有路径和。`然后对其进行排序，这样我们也就可以直接从小到大判断进行并查集。然后在过程中计算出最短路径。有所有路径和减去最短路径既是答案的值。

以下为代码（洛谷所有测试点AC）

#include
#include
#include
using namespace std;
const int N=110,M=N*2+10;
struct Egde
{
 int a,b,c;
 bool operator<(const Egde &w)const//运算符重载，以便于sort函数的运算相当于重写了sort的cmp函数）
 {
  return c<w.c;
 }
}edge[M];
int cnt,p[N],res,all,n,k;
int find(int x)//查找集合的顶端点，及当前点的所在树（即集合）。
{
 if(x!=p[x])return find(p[x]); 
 return p[x];
}
void kruskal()
{
 for(int i=0;i<k;i++)//从小到大循环边
 {
  int a=edge[i].a,b=edge[i].b,c=edge[i].c;
  a=find(a),b=find(b);
  if(a!=b)//如果当前边的左右端点不在同一个树（集合）中进行统一，将a放入b的集合（插入b.的树）。
  {
   p[b]=a;
   res+=c;
   cnt++;
  }
  if(cnt==n-1)break;//当全部点进入集合后结束循环
 }
    printf("%d",all-res);//输出答案
}
int main()
{
 cin>>n>>k;
 for(int i=0;i<k;i++)//对每条边进行输入并计边的权值和。
 {
        scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].c);
  	all+=edge[i].c;
 }
 sort(edge,edge+k);//对边进行排序
 for(int i=1;i<n;i++)p[i]=i;//使每个点都各自处于一个单独的集合（树）中以便于并查集
 kruskal();
 return 0;
}

方法二

prim算法
思路与上方一致，求出最短路径，使用所有路径和减去最短路径即为答案。这里简要介绍下prim算法

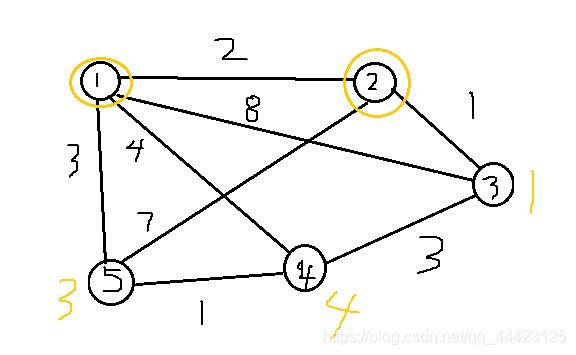
首先如上图我们可以选择1这个点为集合的起始点，然后使用1这个点更新其他点到集合的距离（即最短路径）结构如下图
（橙色字体为点到集合的最短路径，被橙色圈起来的点已经进入集合）

而后选择距离集合最近的点(即点2)加入集合最短路径加上2，并更新到集合的最短路径如下图

重复上诉步骤选择距离集合最近的点(即点3)加入集合最短路径加上1，（最短路径此时为3） 并更新到集合的最短路径如下图

重复上诉步骤选择距离集合最近的点(即点4或点5均可这里我们选择点5)加入集合最短路径加上3，（最短路径此时为6） 并更新到集合的最短路径如下图

最后将点4加入集合中此时最短路径为7

其最小生成树为下图

以下为代码（洛谷所有测试点AC）

#include
#include
#include
using namespace std;
const int N=510;
int dist[N][N],n,m,value[N],all;
bool choose[N];
int prim()
{
    int res=0;
    memset(value,0x3f,sizeof(value));//首先将所有点到集合的距离设置为无限大
    for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)
        if(!choose[j]&&(t==-1||value[t]>value[j]))t=j;//查询到集合最短路径的点
        if(i)res+=value[t];
        choose[t]=true;//该点加入集合
        for(int j=1;j<=n;j++)value[j]=min(value[j],dist[t][j]);//；利用选中点更新各点到集合的最短路径
    }
    return res;
}
int main()
{
    memset(dist,0x3f,sizeof(dist));
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;//因为是双向联通这里是无向图，故当做双向边处理。
        dist[a][b]=min(dist[a][b],c);
        dist[b][a]=min(dist[b][a],c);
        all+=c;//计算所有边权值和
    }
    int b=prim();
    cout<<all-b<<endl;
    return 0;
}