NOI2018情报中心（虚树+线段树合并）

题目链接

题目大意

给定一棵 $n$ 个节点的树，以及 $m$ 条链，每条链有费用，每条边有收益。问选出两条至少一条边重合的链，使链并上的边权和 $-$ 两条链的总费用最大。
$n\le 10^6,m\le 2\times 10^6$。

题解

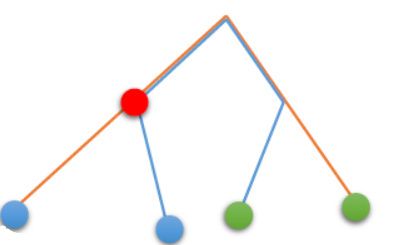
不妨进行分类讨论。首先，如果两条链的 LCA 不是同一个点，那么形成的图应该长这样：（盗个图）

那么它对答案的贡献应该是：两条链的长度和 $-$ 红点深度 $+\max ($绿点深度,蓝点深度$)-$ 两条链的费用。

于是我们枚举红点，不妨设 $f(i,j)$ 表示到点 $i$，经过点 $i$ 且 LCA 在 $j$ 的所有链中，长度 $-$ 费用最大的，$g(i,j)$ 表示长度 $-$ 费用 $+$ LCA深度最大的，那么可以线段树合并维护这个数组，也就是说用左子树的 $f$ 和右子树的 $g$ 来更新答案。

但注意，由于红点是分叉点，更新答案的链必须分属两棵不同的子树。因此在线段树合并的时候要用 $x$ 的左子树和 $y$ 的右子树更新一遍，再用 $x$ 的右子树和 $y$ 的左子树更新一遍就行了。注意到一条链的 LCA 时要先减掉这条链的贡献，总复杂度 $O(nlogn)$。

其次，考虑两个 LCA 相同的情况。那么形成的图应该长这样：（再盗个图）

那么它对答案的贡献应该是：$\frac{1}{2}($两条链长$+$蓝点距离$+$绿点距离$-2$两条链总费用$)$。考虑枚举红点，我们把链长$-2$费用+蓝点深度作为一个绿点的点权，那么我们实际上需要找到红点下分属两个子树中的蓝点，对应绿点的点权和+距离的最大值。

容易发现，由于边权非负（点权的正负性不需要考虑），那么计算两个集合并的最远点对，端点一定在原来两个集合的最远点对中产生。于是可以 $O(1)$ 合并。

因此我们对于所有 LCA 相同的链建虚树，直接在虚树上合并最远点对信息并更新答案即可。这部分复杂度在建虚树的 sort 上，$O(nlogn)$。

因此整个问题也是 $O(nlogn)$ 的了。

代码是真心难写难调……而且我居然打错了 $4$ 次 freopen，该退役了qwq。

#include 
namespace IOStream {
	const int MAXR = 10000000;
	char _READ_[MAXR], _PRINT_[MAXR];
	int _READ_POS_, _PRINT_POS_, _READ_LEN_;
	inline char readc() {
	#ifndef ONLINE_JUDGE
		return getchar();
	#endif
		if (!_READ_POS_) _READ_LEN_ = fread(_READ_, 1, MAXR, stdin);
		char c = _READ_[_READ_POS_++];
		if (_READ_POS_ == MAXR) _READ_POS_ = 0;
		if (_READ_POS_ > _READ_LEN_) return 0;
		return c;
	}
	template<typename T> inline void read(T &x) {
		x = 0; register int flag = 1, c;
		while (((c = readc()) < '0' || c > '9') && c != '-');
		if (c == '-') flag = -1; else x = c - '0';
		while ((c = readc()) >= '0' && c <= '9') x = x * 10 - '0' + c;
		x *= flag;
	}
	template<typename T1, typename ...T2> inline void read(T1 &a, T2&... x) {
		read(a), read(x...);
	}
	inline int reads(char *s) {
		register int len = 0, c;
		while (isspace(c = readc()) || !c);
		s[len++] = c;
		while (!isspace(c = readc()) && c > 0) s[len++] = c;
		s[len] = 0;
		return len;
	}
	inline void ioflush() { fwrite(_PRINT_, 1, _PRINT_POS_, stdout), _PRINT_POS_ = 0; fflush(stdout); }
	inline void printc(char c) {
		if (!c) return;
		_PRINT_[_PRINT_POS_++] = c;
		if (_PRINT_POS_ == MAXR) ioflush();
	}
	inline void prints(const char *s, char c = '\n') {
		for (int i = 0; s[i]; i++) printc(s[i]);
		printc(c);
	}
	template<typename T> inline void print(T x, char c = '\n') {
		if (x < 0) printc('-'), x = -x;
		if (x) {
			static char sta[20];
			register int tp = 0;
			for (; x; x /= 10) sta[tp++] = x % 10 + '0';
			while (tp > 0) printc(sta[--tp]);
		} else printc('0');
		printc(c);
	}
	template<typename T1, typename ...T2> inline void print(T1 x, T2... y) {
		print(x, ' '), print(y...);
	}
}
using namespace IOStream;
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
#define cls(x) memset((x), 0, sizeof(x))

const int MAXN = 100005, MAXT = 2000005;
const ll INF = 1E18;
struct Edge { int to, val, next; } edge[MAXN];
int head[MAXN], st[20][MAXN], dfn[MAXN];
int lev[MAXN], lg[MAXN], id[MAXN], tot, n, m, T;
ll dep[MAXN], srt[MAXN], ans;
void dfs(int u, int fa) {
	st[0][dfn[u] = ++tot] = u, lev[u] = lev[fa] + 1;
	for (int i = head[u]; i; i = edge[i].next) {
		int v = edge[i].to;
		if (v == fa) continue;
		dep[v] = dep[u] + edge[i].val;
		dfs(v, u), st[0][++tot] = u;
	}
}
void addedge(int u, int v, int w) {
	edge[++tot] = (Edge) { v, w, head[u] };
	head[u] = tot;
}
int get_min(int x, int y) { return lev[x] < lev[y] ? x : y; }
int get_lca(int x, int y) {
	x = dfn[x], y = dfn[y];
	if (x > y) swap(x, y);
	int l = lg[y - x + 1];
	return get_min(st[l][x], st[l][y - (1 << l) + 1]);
}
ll get_dis(int x, int y) {
	return dep[x] + dep[y] - dep[get_lca(x, y)] * 2;
}
struct Node { int u; ll w; };
namespace S1 {
	ll mx1[MAXT], mx2[MAXT], now;
	int ls[MAXT], rs[MAXT], rt[MAXN], tot;
	vector<Node> nd[MAXN];
	void pushup(int x) {
		mx1[x] = max(mx1[ls[x]], mx1[rs[x]]);
		mx2[x] = max(mx2[ls[x]], mx2[rs[x]]);
	}
	void inc(int &k, int p, ll x, int l = 1, int r = n) {
		if (!k) k = ++tot, mx1[k] = mx2[k] = -INF;
		if (l == r) {
			mx1[k] = max(mx1[k], x);
			mx2[k] = max(mx2[k], x + srt[l]);
			return;
		}
		int mid = (l + r) >> 1;
		if (p <= mid) inc(ls[k], p, x, l, mid);
		else inc(rs[k], p, x, mid + 1, r);
		pushup(k);
	}
	void dec(int &k, int p, int l = 1, int r = n) {
		if (!k) return;
		if (l == r) { k = 0; return; }
		int mid = (l + r) >> 1;
		if (p <= mid) dec(ls[k], p, l, mid);
		else dec(rs[k], p, mid + 1, r);
		pushup(k);
	}
	int merge(int x, int y, int l = 1, int r = n) {
		if (!x || !y) return x + y;
		if (l == r) {
			mx1[x] = max(mx1[x], mx1[y]);
			mx2[x] = max(mx2[x], mx2[y]);
		} else {
			ans = max(ans, mx1[ls[x]] + mx2[rs[y]] - now);
			ans = max(ans, mx2[rs[x]] + mx1[ls[y]] - now);
			int mid = (l + r) >> 1;
			ls[x] = merge(ls[x], ls[y], l, mid);
			rs[x] = merge(rs[x], rs[y], mid + 1, r);
			pushup(x);
		}
		return x;
	}
	void dfs(int u, int fa) {
		for (int i = head[u]; i; i = edge[i].next)
			if (edge[i].to != fa) dfs(edge[i].to, u);
		now = dep[u];
		for (int i = head[u]; i; i = edge[i].next) {
			int v = edge[i].to;
			if (v == fa) continue;
			dec(rt[v], id[u]);
			rt[u] = merge(rt[u], rt[v]);
		}
		for (const Node &d : nd[u]) {
			int t = 0; inc(t, id[d.u], d.w);
			rt[u] = merge(rt[u], t);
		}
	}
	void solve() {
		mx1[0] = mx2[0] = -INF;
		dfs(1, 0);
		for (int i = 1; i <= tot; i++) {
			ls[i] = rs[i] = 0;
			mx1[i] = mx2[i] = -INF;
		} tot = 0;
		for (int i = 1; i <= n; i++) {
			rt[i] = 0;
			nd[i].clear();
		}
	}
}

namespace S2 {
	struct Pair {
		Node x, y; ll d;
		bool operator<(const Pair &p) const { return d < p.d; }
	} f[MAXN];
	struct Path { int x, y; ll w; };
	vector<Path> nd[MAXN];
	int sta[MAXN], arr[MAXN], now, rt;
	Pair calc(const Node &x, const Node &y) {
		ll d = get_dis(x.u, y.u) + x.w + y.w;
		ans = max(ans, d / 2 - dep[now]);
		return (Pair) { x, y, d };
	}
	void merge(Pair &a, Pair &b) {
		if (a.d == -INF) { a = b; b.d = -INF; return; }
		if (b.d == -INF) return;
		if (now != rt) {
			Pair p = max(calc(a.x, b.x), calc(a.x, b.y));
			p = max(p, max(calc(a.y, b.x), calc(a.y, b.y)));
			a = max(a, max(b, p));
		}
		b.d = -INF;
	}
	void solve(const vector<Path> &vec) {
		int tot = 0, tp = 0;
		rt = get_lca(vec[0].x, vec[0].y);
		for (const Path &p : vec) {
			arr[++tot] = p.x;
			arr[++tot] = p.y;
			Node a = (Node) { p.x, dep[p.y] + p.w };
			Node b = (Node) { p.y, dep[p.x] + p.w };
			Pair x = (Pair) { b, b, b.w << 1 }, y = (Pair) { a, a, a.w << 1 };
			merge(f[now = p.x], x), merge(f[now = p.y], y);
		}
		sort(arr + 1, arr + 1 + tot, [&](int x, int y) { return dfn[x] < dfn[y]; });
		sta[++tp] = arr[1];
		for (int i = 2; i <= tot; i++) if (arr[i] != arr[i - 1]) {
			int p = arr[i], l = get_lca(p, sta[tp]);
			while (tp > 1 && lev[sta[tp - 1]] >= lev[l])
				merge(f[now = sta[tp - 1]], f[sta[tp]]), --tp;
			if (sta[tp] != l) merge(f[now = l], f[sta[tp]]), sta[tp] = l;
			sta[++tp] = p;
		}
		while (tp > 1) merge(f[now = sta[tp - 1]], f[sta[tp]]), --tp;
		f[sta[1]].d = -INF;
	}
	void solve() {
		for (int i = 1; i <= n; i++) f[i].d = -INF;
		for (int i = 1; i <= n; i++)
			if (nd[i].size() > 1) solve(nd[i]);
		for (int i = 1; i <= n; i++) nd[i].clear();
	}
}
int main() {
	freopen("1.in", "r", stdin);
	freopen("out1.txt", "w", stdout);
	for (int i = 2; i < MAXN; i++) lg[i] = lg[i >> 1] + 1;
	int cs = 0;
	for (read(T); T--;) { ++cs;
		tot = 0, ans = -INF;
		read(n);
		for (int i = 1; i <= n; i++) head[i] = 0;
		for (int i = 1; i < n; i++) {
			int u, v, w; read(u, v, w);
			addedge(u, v, w), addedge(v, u, w);
		}
		dfs(1, tot = 0);
		for (int i = 1; i <= n; i++) srt[i] = dep[i];
		sort(srt + 1, srt + 1 + n);
		for (int i = 1; i <= n; i++)
			id[i] = lower_bound(srt + 1, srt + 1 + n, dep[i]) - srt, --srt[id[i]];
		for (int i = 1; i <= n; i++) ++srt[i];
		for (int i = 1; i < 20; i++)
		for (int j = 1; j + (1 << i) - 1 <= tot; j++)
			st[i][j] = get_min(st[i - 1][j], st[i - 1][j + (1 << i >> 1)]);
		read(m);
		for (int i = 1; i <= m; i++) {
			int u, v; ll w; read(u, v, w);
			if (u == v) continue;
			int l = get_lca(u, v); ll d = get_dis(u, v);
			if (u != l) S1::nd[u].push_back((Node) { l, d - w });
			if (v != l) S1::nd[v].push_back((Node) { l, d - w });
			S2::nd[l].push_back((S2::Path) { u, v, d - w * 2 });
		}
		S1::solve();
		S2::solve();
		if (ans < -1E17) prints("F");
		else print(ans);
	}
	ioflush();
	return 0;
}