短波信道模型--多径瑞利信道原理详解及matlab实现

        瑞利衰落是一种小尺度衰落效应，它总是叠加于大尺度衰落效应上如衰减、阴影等。发射端和接收端相对运动速度的大小决定了信道衰落的快慢。相对运对导致接收信号存在多普勒频移，即信道衰落的快慢与多普勒频移的大小有关。

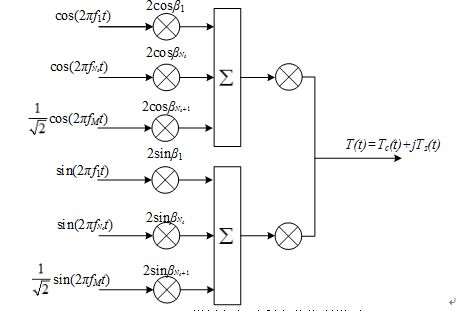
        基于频率单调衰落的基带等效Jakes模型搭建的多径瑞利衰落信道，Jakes仿真模型用多个多普勒频偏和一个最大多普勒频偏模拟多径瑞利衰落信道，其仿真器框图如图所示：

多径瑞利衰落信道的matlab代码为：模拟了6条衰落信道，不同延时，不同衰落功率。直接自己编写的代码，可以自己修改参数，没有使用MATLAB的自带函数，我觉得那个函数，嗯。。。。。，用起来不方便，而且有的时候衰落和延时加不进去。

function [xout]=MUL_RAYLEIGH(x,itau,dlvl,itn,n1,nsamp,tstp,fd,flat)
%****************** variables *************************
% x  input Ich baseband data     
% yout   output Qch baseband data
% itau   : Delay time for each multipath fading
% dlvl   : Attenuation level for each multipath fading
% itn    : Fading counter for each multipath fading
% n1     : Number of summation for direct and delayed waves 
% nsamp   : Total number od symbols
% tstp   : Mininum time resolution
% fd   : Maxmum doppler frequency
% flat     flat fading or not 
% (1->flat (only amplitude is fluctuated),0->nomal(phase and amplitude are fluctutated)   
%******************************************************
n0 = 25;      % n0     : Number of waves in order to generate each multipath fading
xout = zeros(1,nsamp);
total_attn = sum(10 .^(  dlvl ./ 20.0));

for k = 1 : n1 
    
	atts = 10.^ (dlvl(k)/20.0);

	if dlvl(k) >= 40.0 
	       atts = 0.0;
	end

	[xtmp] = delay ( x, nsamp , itau(k));
	[xtmp3] = siglfade (xtmp,nsamp,tstp,fd,n0,itn(k),flat);% single fade
	
  xout = xout + atts .* xtmp3 ./ sqrt(total_attn);

end
% ************************end of file***********************************
function [xout] = delay(x,nsamp,idel )
% Gives delay to input signal
%****************** variables *************************
% x      input Ich data     
% xout   output Qch data
% nsamp   Number of samples to be simulated 
% idel   Number of samples to be delayed
%******************************************************

xout=zeros(1,nsamp);
if idel ~= 0 
  xout(1:idel) = zeros(1,idel);
end

xout(idel+1:nsamp) = x(1:nsamp-idel);

% ************************end of file***********************************

function [xout]=siglfade(x,nsamp,tstp,fd,no,counter,flat)
% Generate Rayleigh fading
% %****************** variables *************************
% x  : input Ich data     
% xout   : output Qch data
% nsamp  : Number of samples to be simulated       
% tstp   : Minimum time resolution                    
% fd     : maximum doppler frequency               
% no     : number of waves in order to generate fading   
% counter  : fading counter                          
% flat     : flat fading or not 
% (1->flat (only amplitude is fluctuated),0->nomal(phase and amplitude are fluctutated)    
%******************************************************

if fd ~= 0.0  
    ac0 = sqrt(1.0 ./ (2.0.*(no + 1)));   % power normalized constant(ich)
    as0 = sqrt(1.0 ./ (2.0.*no));         % power normalized constant(qch)
    ic0 = counter;                        % fading counter
 
    pai = 3.14159265;   
    wm = 2.0.*pai.*fd;
    n = 4.*no + 2;
    ts = tstp;
    wmts = wm.*ts;
    paino = pai./no;                        

    xc=zeros(1,nsamp);
    xs=zeros(1,nsamp);
    ic=[1:nsamp]+ic0;

  for nn = 1: no
	  cwn = cos( cos(2.0.*pai.*nn./n).*ic.*wmts );
	  xc = xc + cos(paino.*nn).*cwn;
	  xs = xs + sin(paino.*nn).*cwn;
  end

  cwmt = sqrt(2.0).*cos(ic.*wmts);
  xc = (2.0.*xc + cwmt).*ac0;
  xs = 2.0.*xs.*as0;

  ramp=sqrt(xc.^2+xs.^2);   

  if flat ==1
    xout = sqrt(xc.^2+xs.^2).*x;    % output signal
  else
    xout = x .*(xc+1i*xs);
  end

else  
  xout = x;
end

% ************************end of file***********************************