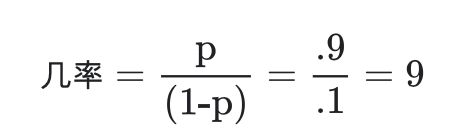MATLAB算法实战应用案例精讲-【数模应用】漫谈机器学习（二）

目录

几个高频面试题目

机器学习中的模型评价、模型选择与算法选择 

基本的模型评估项和技术

Bootstrapping 和不确定性

交叉验证和超参数优化

机器学习的发展历程

知识储备

机器学习常用术语

算法原理 

1. 什么是机器学习？

机器学习和人工智能的关系

机器学习的工作方式

机器学习所处的位置

机器学习的实际应用

机器学习的算法

机器学习的组成

学习 V.S. 智能

机器学习世界的版图

分类算法

算法应用 

---

 

几个高频面试题目

机器学习中的模型评价、模型选择与算法选择 

基本的模型评估项和技术

机器学习已经成为我们生活的中心，无论是作为消费者、客户、研究者还是从业人员。无论将预测建模技术应用到研究还是商业问题，我认为其共同点是：做出足够好的预测。用模型拟合训练数据是一回事，但我们如何了解模型的泛化能力？我们如何确定模型是否只是简单地记忆训练数据，无法对未见过的样本做出好的预测？还有，我们如何选择好的模型呢？也许还有更好的算法可以处理眼前的问题呢？

1.1 性能评估：泛化性能 vs. 模型选择

让我们考虑这个问题：「如何评估机器学习模型的性能？」典型的回答可能是：「首先，将训练数据馈送给学习算法以学习一个模型。第二，预测测试集的标签。第三，计算模型对测试集的预测准确率。」然而，评估模型性能并非那么简单。也许我们应该从不同的角度解决之前的问题：「为什么我们要关心性能评估呢？」理论上，模型的性能评估能给出模型的泛化能力，在未见过的数据上执行预测是应用机器学习或开发新算法的主要问题。通常，机器学习包含大量实验，例如超参数调整。在训练数据集上用不同的超参数设置运行学习算法最终会得到不同的模型。由于我们感兴趣的是从该超参数设置中选择最优性能的模型，因此我们需要找到评估每个模型性能的方法，以将它们进行排序。

我们需要在微调算法之外更进一步，即不仅仅是在给定的环境下实验单个算法，而是对比不同的算法，通常从预测性能和计算性能方面进行比较。我们总结一下评估模型的预测性能的主要作用：

• 评估模型的泛化性能，即模型泛化到未见过数据的能力；

• 通过调整学习算法和在给定的假设空间中选择性能最优的模型，以提升预测性能；

• 确定最适用于待解决问题的机器学习算法。因此，我们可以比较不同的算法，选择其中性能最优的模型；或者选择算法的假设空间中的性能最优模型。

虽然上面列出的三个子任务都是为了评估模型的性能，但是它们需要使用的方法是不同的。本文将概述解决这些子任务需要的不同方法。

我们当然希望尽可能精确地预测模型的泛化性能。然而，本文的一个要点就是，如果偏差对所有模型的影响是等价的，那么偏差性能评估基本可以完美地进行模型选择和算法选择。如果要用排序选择最优的模型或算法，我们只需要知道它们的相对性能就可以了。例如，如果所有的性能评估都是有偏差的，并且低估了它们的性能（10%），这不会影响最终的排序。更具体地说，如果我们得到如下三个模型，这些模型的预测准确率如下：

M2: 75% > M1: 70% > M3: 65

如果我们添加了 10% 的性能偏差（低估），则三种模型的排序没有发生改变：

M2: 65% > M1: 60% > M3: 55%. 

但是，注意如果最佳模型（M2）的泛化准确率是 65%，很明显这个精度是非常低的。评估模型的绝对性能可能是机器学习中最难的任务之一。

图 2：留出验证方法的图示。

Bootstrapping 和不确定性

本章介绍一些用于模型评估的高级技术。我们首先讨论用来评估模型性能不确定性和模型方差、稳定性的技术。之后我们将介绍交叉验证方法用于模型选择。如第一章所述，关于我们为什么要关心模型评估，存在三个相关但不同的任务或原因。

• 我们想评估泛化准确度，即模型在未见数据上的预测性能。

• 我们想通过调整学习算法、从给定假设空间中选择性能最好的模型，来改善预测性能。

• 我们想确定手头最适合待解决问题的机器学习算法。因此，我们想对比不同的算法，选出性能最好的一个；或从算法的假设空间中选出性能最好的模型。

图 3：偏差和方差的不同组合的图示。

图 4：在 MNIST 数据集上 softmax 分类器的学习曲线。

图 5：二维高斯分布中的重复子采样。

交叉验证和超参数优化

几乎所有机器学习算法都需要我们机器学习研究者和从业者指定大量设置。这些超参数帮助我们控制机器学习算法在优化性能、找出偏差方差最佳平衡时的行为。用于性能优化的超参数调整本身就是一门艺术，没有固定规则可以保证在给定数据集上的性能最优。前面的章节提到了用于评估模型泛化性能的留出技术和 bootstrap 技术。偏差-方差权衡和计算性能估计的不稳定性方法都得到了介绍。本章主要介绍用于模型评估和选择的不同交叉验证方法，包括对不同超参数配置的模型进行排序和评估其泛化至独立数据集的性能。

本章生成图像的代码详见：https://github.com/rasbt/model-eval-article-supplementary/blob/master/code/resampling-and-kfold.ipynb。

图 11：logistic 回归的概念图示。

我们可以把超参数调整（又称超参数优化）和模型选择的过程看作元优化任务。当学习算法在训练集上优化目标函数时（懒惰学习器是例外），超参数优化是基于它的另一项任务。这里，我们通常想优化性能指标，如分类准确度或接受者操作特征曲线（ROC 曲线）下面积。超参数调整阶段之后，基于测试集性能选择模型似乎是一种合理的方法。但是，多次重复使用测试集可能会带来偏差和最终性能估计，且可能导致对泛化性能的预期过分乐观，可以说是「测试集泄露信息」。为了避免这个问题，我们可以使用三次分割（three-way split），将数据集分割成训练集、验证集和测试集。对超参数调整和模型选择进行训练-验证可以保证测试集「独立」于模型选择。这里，我们再回顾一下性能估计的「3 个目标」：

• 我们想评估泛化准确度，即模型在未见数据上的预测性能。

• 我们想通过调整学习算法、从给定假设空间中选择性能最好的模型，来改善预测性能。

• 我们想确定最适合待解决问题的机器学习算法。因此，我们想对比不同的算法，选出性能最好的一个，从算法的假设空间中选出性能最好的模型。

图 12：超参数调整中三路留出方法（three-way holdout method）图示。

图 13：k 折交叉验证步骤图示。

图 16：模型选择中 k 折交叉验证的图示。

机器学习的发展历程

1980 年代

• 主导流派：符号主义；

• 架构：服务器或大型机；

• 主导理论：知识工程；

• 基本决策逻辑：决策支持系统，实用性有限。

1990 年代到 2000 年

• 主导流派：贝叶斯；

• 架构：小型服务器集群；

• 主导理论：概率论；

• 分类：可扩展的比较或对比，对许多任务都足够好了。

2010 年代早期到中期

• 主导流派：联结主义；

• 架构：大型服务器农场；

• 主导理论：神经科学和概率；

• 识别：更加精准的图像和声音识别、翻译、情绪分析等。

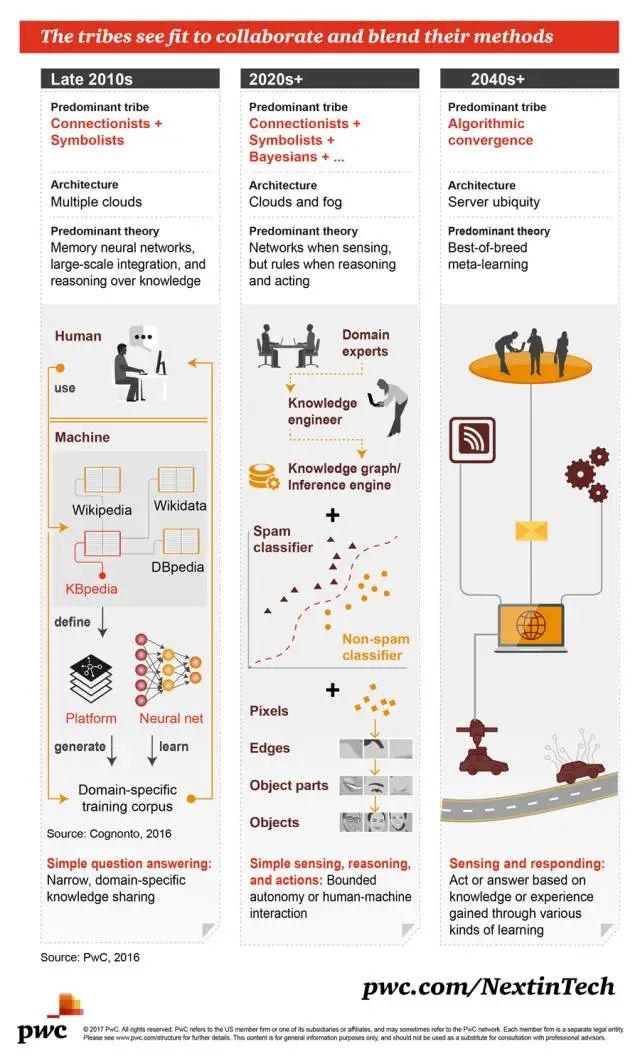
2010 年代末期

• 主导流派：联结主义+符号主义；

• 架构：许多云；

• 主导理论：记忆神经网络、大规模集成、基于知识的推理；

• 简单的问答：范围狭窄的、领域特定的知识共享。

2020 年代+

• 主导流派：联结主义+符号主义+贝叶斯+……；

• 架构：云计算和雾计算；

• 主导理论：感知的时候有网络，推理和工作的时候有规则；

• 简单感知、推理和行动：有限制的自动化或人机交互。

2040 年代+

• 主导流派：算法融合；

• 架构：无处不在的服务器；

• 主导理论：最佳组合的元学习；

• 感知和响应：基于通过多种学习方式获得的知识或经验采取行动或做出回答。

知识储备

机器学习常用术语

A

• A/B 测试 (A/B testing)

一种统计方法，用于将两种或多种技术进行比较，通常是将当前采用的技术与新技术进行比较。A/B 测试不仅旨在确定哪种技术的效果更好，而且还有助于了解相应差异是否具有显著的统计意义。A/B 测试通常是采用一种衡量方式对两种技术进行比较，但也适用于任意有限数量的技术和衡量方式。

• 准确率 (accuracy)

分类模型的正确预测所占的比例。在多类别分类中，准确率的定义如下：

在二元分类中，准确率的定义如下：

请参阅正例和负例。

• 激活函数 (activation function)

一种函数（例如ReLU或S 型函数），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

• AdaGrad

一种先进的梯度下降法，用于重新调整每个参数的梯度，以便有效地为每个参数指定独立的学习速率。如需查看完整的解释，请参阅这篇论文。

• ROC 曲线下面积 (AUC, Area under the ROC Curve)

一种会考虑所有可能分类阈值的评估指标。

ROC 曲线下面积是，对于随机选择的正类别样本确实为正类别，以及随机选择的负类别样本为正类别，分类器更确信前者的概率。

---

B

• 反向传播算法 (backpropagation)

在神经网络上执行梯度下降法的主要算法。该算法会先按前向传播方式计算（并缓存）每个节点的输出值，然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。

• 基准 (baseline)

一种简单的模型或启发法，用作比较模型效果时的参考点。基准有助于模型开发者针对特定问题量化最低预期效果。

• 批次 (batch)

模型训练的一次迭代（即一次梯度更新）中使用的样本集。

另请参阅批次大小。

• 批次大小 (batch size)

一个批次中的样本数。例如，SGD的批次大小为 1，而小批次的大小通常介于 10 到 1000 之间。批次大小在训练和推断期间通常是固定的；不过，TensorFlow 允许使用动态批次大小。

• 偏差 (bias)

距离原点的截距或偏移。偏差（也称为偏差项）在机器学习模型中用  或  表示。例如，在下面的公式中，偏差为 ：

请勿与预测偏差混淆。

• 二元分类 (binary classification)

一种分类任务，可输出两种互斥类别之一。例如，对电子邮件进行评估并输出“垃圾邮件”或“非垃圾邮件”的机器学习模型就是一个二元分类器。

• 分箱 (binning)

请参阅分桶。

• 分桶 (bucketing)

将一个特征（通常是连续特征）转换成多个二元特征（称为桶或箱），通常根据值区间进行转换。例如，您可以将温度区间分割为离散分箱，而不是将温度表示成单个连续的浮点特征。假设温度数据可精确到小数点后一位，则可以将介于 0.0 到 15.0 度之间的所有温度都归入一个分箱，将介于 15.1 到 30.0 度之间的所有温度归入第二个分箱，并将介于 30.1 到 50.0 度之间的所有温度归入第三个分箱。

---

C

• 校准层 (calibration layer)

一种预测后调整，通常是为了降低预测偏差的影响。调整后的预测和概率应与观察到的标签集的分布一致。

• 候选采样 (candidate sampling)

一种训练时进行的优化，会使用某种函数（例如 softmax）针对所有正类别标签计算概率，但对于负类别标签，则仅针对其随机样本计算概率。例如，如果某个样本的标签为“小猎犬”和“狗”，则候选采样将针对“小猎犬”和“狗”类别输出以及其他类别（猫、棒棒糖、栅栏）的随机子集计算预测概率和相应的损失项。这种采样基于的想法是，只要正类别始终得到适当的正增强，负类别就可以从频率较低的负增强中进行学习，这确实是在实际中观察到的情况。候选采样的目的是，通过不针对所有负类别计算预测结果来提高计算效率。

• 分类数据 (categorical data)

一种特征，拥有一组离散的可能值。以某个名为 house style 的分类特征为例，该特征拥有一组离散的可能值（共三个），即 Tudor, ranch, colonial。通过将 house style 表示成分类数据，相应模型可以学习 Tudor、ranch 和 colonial 分别对房价的影响。

有时，离散集中的值是互斥的，只能将其中一个值应用于指定样本。例如，car maker 分类特征可能只允许一个样本有一个值 (Toyota)。在其他情况下，则可以应用多个值。一辆车可能会被喷涂多种不同的颜色，因此，car color 分类特征可能会允许单个样本具有多个值（例如 red 和 white）。

分类特征有时称为离散特征。

与数值数据相对。

• 形心 (centroid)

聚类的中心，由k-means或k-median算法决定。例如，如果 k 为 3，则 k-means 或 k-median 算法会找出 3 个形心。

• 检查点 (checkpoint)

一种数据，用于捕获模型变量在特定时间的状态。借助检查点，可以导出模型权重，跨多个会话执行训练，以及使训练在发生错误之后得以继续（例如作业抢占）。请注意，图本身不包含在检查点中。

• 类别 (class)

为标签枚举的一组目标值中的一个。例如，在检测垃圾邮件的二元分类模型中，两种类别分别是“垃圾邮件”和“非垃圾邮件”。在识别狗品种的多类别分类模型中，类别可以是“贵宾犬”、“小猎犬”、“哈巴犬”等等。

• 分类不平衡的数据集 (class-imbalanced data set)

一种二元分类问题，在此类问题中，两种类别的标签在出现频率方面具有很大的差距。例如，在某个疾病数据集中，0.0001 的样本具有正类别标签，0.9999 的样本具有负类别标签，这就属于分类不平衡问题；但在某个足球比赛预测器中，0.51 的样本的标签为其中一个球队赢，0.49 的样本的标签为另一个球队赢，这就不属于分类不平衡问题。

• 分类模型 (classification model)

一种机器学习模型，用于区分两种或多种离散类别。例如，某个自然语言处理分类模型可以确定输入的句子是法语、西班牙语还是意大利语。请与回归模型进行比较。

• 分类阈值 (classification threshold)

一种标量值条件，应用于模型预测的得分，旨在将正类别与负类别区分开。将逻辑回归结果映射到二元分类时使用。以某个逻辑回归模型为例，该模型用于确定指定电子邮件是垃圾邮件的概率。如果分类阈值为 0.9，那么逻辑回归值高于 0.9 的电子邮件将被归类为“垃圾邮件”，低于 0.9 的则被归类为“非垃圾邮件”。

• 聚类 (clustering)

将关联的样本分成一组，一般用于非监督式学习。在所有样本均分组完毕后，相关人员便可选择性地为每个聚类赋予含义。

聚类算法有很多。例如，k-means 算法会基于样本与形心的接近程度聚类样本，如下图所示：

之后，研究人员便可查看这些聚类并进行其他操作，例如，将聚类 1 标记为“矮型树”，将聚类 2 标记为“全尺寸树”。

再举一个例子，例如基于样本与中心点距离的聚类算法，如下所示：

• 协同过滤 (collaborative filtering)

根据很多其他用户的兴趣来预测某位用户的兴趣。协同过滤通常用在推荐系统中。

• 混淆矩阵 (confusion matrix)

一种 NxN 表格，用于总结分类模型的预测效果；即标签和模型预测的分类之间的关联。在混淆矩阵中，一个轴表示模型预测的标签，另一个轴表示实际标签。N 表示类别个数。在二元分类问题中，N=2。例如，下面显示了一个二元分类问题的混淆矩阵示例：

上面的混淆矩阵显示，在 19 个实际有肿瘤的样本中，该模型正确地将 18 个归类为有肿瘤（18 个正例），错误地将 1 个归类为没有肿瘤（1 个假负例）。同样，在 458 个实际没有肿瘤的样本中，模型归类正确的有 452 个（452 个负例），归类错误的有 6 个（6 个假正例）。

多类别分类问题的混淆矩阵有助于确定出错模式。例如，某个混淆矩阵可以揭示，某个经过训练以识别手写数字的模型往往会将 4 错误地预测为 9，将 7 错误地预测为 1。

混淆矩阵包含计算各种效果指标（包括精确率和召回率）所需的充足信息。

• 连续特征 (continuous feature)

一种浮点特征，可能值的区间不受限制。与离散特征相对。

• 收敛 (convergence)

通俗来说，收敛通常是指在训练期间达到的一种状态，即经过一定次数的迭代之后，训练损失和验证损失在每次迭代中的变化都非常小或根本没有变化。也就是说，如果采用当前数据进行额外的训练将无法改进模型，模型即达到收敛状态。在深度学习中，损失值有时会在最终下降之前的多次迭代中保持不变或几乎保持不变，暂时形成收敛的假象。

另请参阅早停法。

另请参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization（《凸优化》）。

• 凸函数 (convex function)

一种函数，函数图像以上的区域为凸集。典型凸函数的形状类似于字母U。例如，以下都是凸函数：

相反，以下函数则不是凸函数。请注意图像上方的区域如何不是凸集：

严格凸函数只有一个局部最低点，该点也是全局最低点。经典的 U 形函数都是严格凸函数。不过，有些凸函数（例如直线）则不是这样。

很多常见的损失函数（包括下列函数）都是凸函数：

• L2 损失函数

• 对数损失函数

• L1 正则化

• L2 正则化

梯度下降法的很多变体都一定能找到一个接近严格凸函数最小值的点。同样，随机梯度下降法的很多变体都有很高的可能性能够找到接近严格凸函数最小值的点（但并非一定能找到）。

两个凸函数的和（例如 L2 损失函数 + L1 正则化）也是凸函数。

深度模型绝不会是凸函数。值得注意的是，专门针对凸优化设计的算法往往总能在深度网络上找到非常好的解决方案，虽然这些解决方案并不一定对应于全局最小值。

• 凸优化 (convex optimization)

使用数学方法（例如梯度下降法）寻找凸函数最小值的过程。机器学习方面的大量研究都是专注于如何通过公式将各种问题表示成凸优化问题，以及如何更高效地解决这些问题。

如需完整的详细信息，请参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization（《凸优化》）。

• 凸集 (convex set)

欧几里得空间的一个子集，其中任意两点之间的连线仍完全落在该子集内。例如，下面的两个图形都是凸集：

相反，下面的两个图形都不是凸集：

• 卷积 (convolution)

简单来说，卷积在数学中指两个函数的组合。在机器学习中，卷积结合使用卷积过滤器和输入矩阵来训练权重。

机器学习中的“卷积”一词通常是卷积运算或卷积层的简称。

如果没有卷积，机器学习算法就需要学习大张量中每个单元格各自的权重。例如，用 2K x 2K 图像训练的机器学习算法将被迫找出 400 万个单独的权重。而使用卷积，机器学习算法只需在卷积过滤器中找出每个单元格的权重，大大减少了训练模型所需的内存。在应用卷积过滤器后，它只需跨单元格进行复制，每个单元格都会与过滤器相乘。

• 卷积过滤器 (convolutional filter)

卷积运算中的两个参与方之一。（另一个参与方是输入矩阵切片。）卷积过滤器是一种矩阵，其等级与输入矩阵相同，但形状小一些。以 28×28 的输入矩阵为例，过滤器可以是小于 28×28 的任何二维矩阵。

在图形操作中，卷积过滤器中的所有单元格通常按照固定模式设置为 1 和 0。在机器学习中，卷积过滤器通常先选择随机数字，然后由网络训练出理想值。

• 卷积层 (convolutional layer)

深度神经网络的一个层，卷积过滤器会在其中传递输入矩阵。以下面的 3x3卷积过滤器为例：

下面的动画显示了一个由 9 个卷积运算（涉及 5x5 输入矩阵）组成的卷积层。请注意，每个卷积运算都涉及一个不同的 3x3 输入矩阵切片。由此产生的 3×3 矩阵（右侧）就包含 9 个卷积运算的结果：

• 卷积神经网络 (convolutional neural network)

一种神经网络，其中至少有一层为卷积层。典型的卷积神经网络包含以下几层的组合：

• 卷积层

• 池化层

• 密集层

卷积神经网络在解决某些类型的问题（如图像识别）上取得了巨大成功。

• 卷积运算 (convolutional operation)

如下所示的两步数学运算：

1. 对卷积过滤器和输入矩阵切片执行元素级乘法。（输入矩阵切片与卷积过滤器具有相同的等级和大小。）

2. 对生成的积矩阵中的所有值求和。

以下面的 5x5 输入矩阵为例：

现在，以下面这个 2x2 卷积过滤器为例：

每个卷积运算都涉及一个 2x2 输入矩阵切片。例如，假设我们使用输入矩阵左上角的 2x2 切片。这样一来，对此切片进行卷积运算将如下所示：

卷积层由一系列卷积运算组成，每个卷积运算都针对不同的输入矩阵切片。

• 成本 (cost)

与损失的含义相同。

• 交叉熵 (cross-entropy)

对数损失函数向多类别分类问题的一种泛化。交叉熵可以量化两种概率分布之间的差异。另请参阅困惑度。

• 自定义 Estimator (custom Estimator)

您按照这些说明自行编写的 Estimator。

与预创建的 Estimator 相对。

---

D

• 数据分析 (data analysis)

根据样本、测量结果和可视化内容来理解数据。数据分析在首次收到数据集、构建第一个模型之前特别有用。此外，数据分析在理解实验和调试系统问题方面也至关重要。

• DataFrame

一种热门的数据类型，用于表示 Pandas 中的数据集。DataFrame 类似于表格。DataFrame 的每一列都有一个名称（标题），每一行都由一个数字标识。

• 数据集 (data set)

一组样本的集合。

• Dataset API (tf.data)

一种高级别的 TensorFlow API，用于读取数据并将其转换为机器学习算法所需的格式。tf.data.Dataset 对象表示一系列元素，其中每个元素都包含一个或多个张量。tf.data.Iterator对象可获取 Dataset 中的元素。

如需详细了解 Dataset API，请参阅《TensorFlow 编程人员指南》中的导入数据。

• 决策边界 (decision boundary)

在二元分类或多类别分类问题中，模型学到的类别之间的分界线。例如，在以下表示某个二元分类问题的图片中，决策边界是橙色类别和蓝色类别之间的分界线：

• 密集层 (dense layer)

与全连接层的含义相同。

• 深度模型 (deep model)

一种神经网络，其中包含多个隐藏层。深度模型依赖于可训练的非线性关系。

与宽度模型相对。

• 密集特征 (dense feature)

一种大部分值是非零值的特征，通常是浮点值张量。与稀疏特征相对。

• 设备 (device)

一类可运行 TensorFlow 会话的硬件，包括 CPU、GPU 和 TPU。

• 离散特征 (discrete feature)

一种特征，包含有限个可能值。例如，某个值只能是“动物”、“蔬菜”或“矿物”的特征便是一个离散特征（或分类特征）。与连续特征相对。

• 丢弃正则化 (dropout regularization)

正则化的一种形式，在训练神经网络方面非常有用。丢弃正则化的运作机制是，在一个梯度步长中移除从神经网络层中随机选择的固定数量的单元。丢弃的单元越多，正则化效果就越强。这类似于训练神经网络以模拟较小网络的指数级规模集成学习。如需完整的详细信息，请参阅Dropout: A Simple Way to Prevent Neural Networks from Overfitting（《丢弃：一种防止神经网络过拟合的简单方法》）。

• 动态模型 (dynamic model)

一种模型，以持续更新的方式在线接受训练。也就是说，数据会源源不断地进入这种模型。

---

E

• 早停法 (early stopping)

一种正则化方法，是指在训练损失仍可以继续降低之前结束模型训练。使用早停法时，您会在验证数据集的损失开始增大（也就是泛化效果变差）时结束模型训练。

• 嵌套 (embeddings)

一种分类特征，以连续值特征表示。通常，嵌套是指将高维度向量映射到低维度的空间。例如，您可以采用以下两种方式之一来表示英文句子中的单词：

• 表示成包含百万个元素（高维度）的稀疏向量，其中所有元素都是整数。向量中的每个单元格都表示一个单独的英文单词，单元格中的值表示相应单词在句子中出现的次数。由于单个英文句子包含的单词不太可能超过 50 个，因此向量中几乎每个单元格都包含 0。少数非 0 的单元格中将包含一个非常小的整数（通常为 1），该整数表示相应单词在句子中出现的次数。

• 表示成包含数百个元素（低维度）的密集向量，其中每个元素都存储一个介于 0 到 1 之间的浮点值。这就是一种嵌套。

在 TensorFlow 中，会按反向传播损失训练嵌套，和训练神经网络中的任何其他参数一样。

• 经验风险最小化 (ERM, empirical risk minimization)

用于选择可以将基于训练集的损失降至最低的函数。与结构风险最小化相对。

• 集成学习 (ensemble)

多个模型的预测结果的并集。您可以通过以下一项或多项来创建集成学习：

• 不同的初始化

• 不同的超参数

• 不同的整体结构

深度模型和宽度模型属于一种集成学习。

• 周期 (epoch)

在训练时，整个数据集的一次完整遍历，以便不漏掉任何一个样本。因此，一个周期表示（N/批次大小）次训练迭代，其中N是样本总数。

• Estimator

tf.Estimator类的一个实例，用于封装负责构建 TensorFlow 图并运行 TensorFlow 会话的逻辑。您可以创建自定义 Estimator（如需相关介绍，请点击此处），也可以实例化其他人预创建的 Estimator。

• 样本 (example)

数据集的一行。一个样本包含一个或多个特征，此外还可能包含一个标签。另请参阅有标签样本和无标签样本。

---

F

• 假负例 (FN, false negative)

被模型错误地预测为负类别的样本。例如，模型推断出某封电子邮件不是垃圾邮件（负类别），但该电子邮件其实是垃圾邮件。

• 假正例 (FP, false positive)

被模型错误地预测为正类别的样本。例如，模型推断出某封电子邮件是垃圾邮件（正类别），但该电子邮件其实不是垃圾邮件。

• 假正例率（false positive rate, 简称 FP 率）

ROC 曲线中的 x 轴。FP 率的定义如下：

• 特征 (feature)

在进行预测时使用的输入变量。

• 特征列 (tf.feature_column)

指定模型应该如何解读特定特征的一种函数。此类函数的输出结果是所有 Estimators 构造函数的必需参数。

借助 tf.feature_column 函数，模型可对输入特征的不同表示法轻松进行实验。有关详情，请参阅《TensorFlow 编程人员指南》中的特征列一章。

“特征列”是 Google 专用的术语。特征列在 Yahoo/Microsoft 使用的 VW 系统中称为“命名空间”，也称为场。

• 特征组合 (feature cross)

通过将单独的特征进行组合（求笛卡尔积）而形成的合成特征。特征组合有助于表达非线性关系。

• 特征工程 (feature engineering)

指以下过程：确定哪些特征可能在训练模型方面非常有用，然后将日志文件及其他来源的原始数据转换为所需的特征。在 TensorFlow 中，特征工程通常是指将原始日志文件条目转换为 tf.Example 协议缓冲区。另请参阅 tf.Transform。

特征工程有时称为特征提取。

• 特征集 (feature set)

训练机器学习模型时采用的一组特征。例如，对于某个用于预测房价的模型，邮政编码、房屋面积以及房屋状况可以组成一个简单的特征集。

• 特征规范 (feature spec)

用于描述如何从 tf.Example 协议缓冲区提取特征数据。由于 tf.Example 协议缓冲区只是一个数据容器，因此您必须指定以下内容：

• 要提取的数据（即特征的键）

• 数据类型（例如 float 或 int）

• 长度（固定或可变）

Estimator API 提供了一些可用来根据给定 FeatureColumns 列表生成特征规范的工具。

• 少量样本学习 (few-shot learning)

一种机器学习方法（通常用于对象分类），旨在仅通过少量训练样本学习有效的分类器。

另请参阅单样本学习。

• 完整 softmax (full softmax)

请参阅 softmax。与候选采样相对。

• 全连接层 (fully connected layer)

一种隐藏层，其中的每个节点均与下一个隐藏层中的每个节点相连。

全连接层又称为密集层。

---

G

• 泛化 (generalization)

指的是模型依据训练时采用的数据，针对以前未见过的新数据做出正确预测的能力。

• 广义线性模型 (generalized linear model)

最小二乘回归模型（基于高斯噪声）向其他类型的模型（基于其他类型的噪声，例如泊松噪声或分类噪声）进行的一种泛化。广义线性模型的示例包括：

• 逻辑回归

• 多类别回归

• 最小二乘回归

可以通过凸优化找到广义线性模型的参数。

广义线性模型具有以下特性：

• 最优的最小二乘回归模型的平均预测结果等于训练数据的平均标签。

• 最优的逻辑回归模型预测的平均概率等于训练数据的平均标签。

广义线性模型的功能受其特征的限制。与深度模型不同，广义线性模型无法“学习新特征”。

• 梯度 (gradient)

偏导数相对于所有自变量的向量。在机器学习中，梯度是模型函数偏导数的向量。梯度指向最高速上升的方向。

• 梯度裁剪 (gradient clipping)

在应用梯度值之前先设置其上限。梯度裁剪有助于确保数值稳定性以及防止梯度爆炸。

• 梯度下降法 (gradient descent)

一种通过计算并且减小梯度将损失降至最低的技术，它以训练数据为条件，来计算损失相对于模型参数的梯度。通俗来说，梯度下降法以迭代方式调整参数，逐渐找到权重和偏差的最佳组合，从而将损失降至最低。

• 图 (graph)

TensorFlow 中的一种计算规范。图中的节点表示操作。边缘具有方向，表示将某项操作的结果（一个张量）作为一个操作数传递给另一项操作。可以使用 TensorBoard 直观呈现图。

---

H

• 启发法 (heuristic)

一种非最优但实用的问题解决方案，足以用于进行改进或从中学习。

• 隐藏层 (hidden layer)

神经网络中的合成层，介于输入层（即特征）和输出层（即预测）之间。神经网络包含一个或多个隐藏层。

• 合页损失函数 (hinge loss)

一系列用于分类的损失函数，旨在找到距离每个训练样本都尽可能远的决策边界，从而使样本和边界之间的裕度最大化。KSVM 使用合页损失函数（或相关函数，例如平方合页损失函数）。对于二元分类，合页损失函数的定义如下：

其中“y'”表示分类器模型的原始输出：

“y”表示真标签，值为 -1 或 +1。

因此，合页损失与 (y * y') 的关系图如下所示：

• 维持数据 (holdout data)

训练期间故意不使用（“维持”）的样本。验证数据集和测试数据集都属于维持数据。维持数据有助于评估模型向训练时所用数据之外的数据进行泛化的能力。与基于训练数据集的损失相比，基于维持数据集的损失有助于更好地估算基于未见过的数据集的损失。

• 超参数 (hyperparameter)

在模型训练的连续过程中，您调节的“旋钮”。例如，学习速率就是一种超参数。

与参数相对。

• 超平面 (hyperplane)

将一个空间划分为两个子空间的边界。例如，在二维空间中，直线就是一个超平面，在三维空间中，平面则是一个超平面。在机器学习中更典型的是：超平面是分隔高维度空间的边界。核支持向量机利用超平面将正类别和负类别区分开来（通常是在极高维度空间中）。

---

I

• 独立同等分布 (i.i.d, independently and identically distributed)

从不会改变的分布中提取的数据，其中提取的每个值都不依赖于之前提取的值。i.i.d. 是机器学习的理想气体 - 一种实用的数学结构，但在现实世界中几乎从未发现过。例如，某个网页的访问者在短时间内的分布可能为 i.i.d.，即分布在该短时间内没有变化，且一位用户的访问行为通常与另一位用户的访问行为无关。不过，如果将时间窗口扩大，网页访问者的分布可能呈现出季节性变化。

• 推断 (inference)

在机器学习中，推断通常指以下过程：通过将训练过的模型应用于无标签样本来做出预测。在统计学中，推断是指在某些观测数据条件下拟合分布参数的过程。（请参阅维基百科中有关统计学推断的文章。）

• 输入函数 (input function)

在 TensorFlow 中，用于将输入数据返回到 Estimator 的训练、评估或预测方法的函数。例如，训练输入函数会返回训练集中的一批特征和标签。

• 输入层 (input layer)

神经网络中的第一层（接收输入数据的层）。

• 实例 (instance)

与样本的含义相同。

• 可解释性 (interpretability)

模型的预测可解释的难易程度。深度模型通常不可解释，也就是说，很难对深度模型的不同层进行解释。相比之下，线性回归模型和宽度模型的可解释性通常要好得多。

• 评分者间一致性信度 (inter-rater agreement)

一种衡量指标，用于衡量在执行某项任务时评分者达成一致的频率。如果评分者未达成一致，则可能需要改进任务说明。有时也称为注释者间一致性信度或评分者间可靠性信度。另请参阅 Cohen's kappa（最热门的评分者间一致性信度衡量指标之一）。

• 迭代 (iteration)

模型的权重在训练期间的一次更新。迭代包含计算参数在单批次数据上的梯度损失。

---

K

• k-means

一种热门的聚类算法，用于对非监督式学习中的样本进行分组。k-means 算法基本上会执行以下操作：

• 以迭代方式确定最佳的 k 中心点（称为形心）。

• 将每个样本分配到最近的形心。与同一个形心距离最近的样本属于同一个组。

k-means 算法会挑选形心位置，以最大限度地减小每个样本与其最接近形心之间的距离的累积平方。

以下面的小狗高度与小狗宽度的关系图为例：

如果 k=3，则 k-means 算法会确定三个形心。每个样本都被分配到与其最接近的形心，最终产生三个组：

假设制造商想要确定小、中和大号狗毛衣的理想尺寸。在该聚类中，三个形心用于标识每只狗的平均高度和平均宽度。因此，制造商可能应该根据这三个形心确定毛衣尺寸。请注意，聚类的形心通常不是聚类中的样本。

上图显示了 k-means 应用于仅具有两个特征（高度和宽度）的样本。请注意，k-means 可以跨多个特征为样本分组。

• k-median

与 k-means 紧密相关的聚类算法。两者的实际区别如下：

• 对于 k-means，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的距离平方和。

• 对于 k-median，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的距离总和。

请注意，距离的定义也有所不同：

• k-means 采用从形心到样本的欧几里得距离。（在二维空间中，欧几里得距离即使用勾股定理来计算斜边。）例如，(2,2) 与 (5,-2) 之间的 k-means 距离为：

• k-median 采用从形心到样本的曼哈顿距离。这个距离是每个维度中绝对差异值的总和。例如，(2,2) 与 (5,-2) 之间的 k-median 距离为：

• Keras

一种热门的 Python 机器学习 API。Keras 能够在多种深度学习框架上运行，其中包括 TensorFlow（在该框架上，Keras 作为 tf.keras 提供）。

• 核支持向量机 (KSVM, Kernel Support Vector Machines)

一种分类算法，旨在通过将输入数据向量映射到更高维度的空间，来最大化正类别和负类别之间的裕度。以某个输入数据集包含一百个特征的分类问题为例。为了最大化正类别和负类别之间的裕度，KSVM 可以在内部将这些特征映射到百万维度的空间。KSVM 使用合页损失函数。

---

L

• L1 损失函数 (L₁ loss)

一种损失函数，基于模型预测的值与标签的实际值之差的绝对值。与 L2 损失函数相比，L1 损失函数对离群值的敏感性弱一些。

• L1 正则化 (L₁ regularization)

一种正则化，根据权重的绝对值的总和来惩罚权重。在依赖稀疏特征的模型中，L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0，从而将这些特征从模型中移除。与 L2 正则化相对。

• L2 损失函数 (L₂ loss)

请参阅平方损失函数。

• L2 正则化 (L₂ regularization)

一种正则化，根据权重的平方和来惩罚权重。L2 正则化有助于使离群值（具有较大正值或较小负值）权重接近于 0，但又不正好为 0。（与 L1 正则化相对。）在线性模型中，L2 正则化始终可以改进泛化。

• 标签 (label)

在监督式学习中，标签指样本的“答案”或“结果”部分。有标签数据集中的每个样本都包含一个或多个特征以及一个标签。例如，在房屋数据集中，特征可能包括卧室数、卫生间数以及房龄，而标签则可能是房价。在垃圾邮件检测数据集中，特征可能包括主题行、发件人以及电子邮件本身，而标签则可能是“垃圾邮件”或“非垃圾邮件”。

• 有标签样本 (labeled example)

包含特征和标签的样本。在监督式训练中，模型从有标签样本中学习规律。

• lambda

与正则化率的含义相同。

（多含义术语，我们在此关注的是该术语在正则化中的定义。）

• 层 (layer)

神经网络中的一组神经元，负责处理一组输入特征，或一组神经元的输出。

此外还指 TensorFlow 中的抽象层。层是 Python 函数，以张量和配置选项作为输入，然后生成其他张量作为输出。当必要的张量组合起来后，用户便可以通过模型函数将结果转换为 Estimator。

• Layers API (tf.layers)

一种 TensorFlow API，用于以层组合的方式构建深度神经网络。通过 Layers API，您可以构建不同类型的层，例如：

• 通过 tf.layers.Dense 构建全连接层。

• 通过 tf.layers.Conv2D 构建卷积层。

在编写自定义 Estimator 时，您可以编写“层”对象来定义所有隐藏层的特征。

Layers API 遵循 Keras layers API 规范。也就是说，除了前缀不同以外，Layers API 中的所有函数均与 Keras layers API 中的对应函数具有相同的名称和签名。

• 学习速率 (learning rate)

在训练模型时用于梯度下降的一个标量。在每次迭代期间，梯度下降法都会将学习速率与梯度相乘。得出的乘积称为梯度步长。

学习速率是一个重要的超参数。

• 最小二乘回归 (least squares regression)

一种通过最小化 L2 损失训练出的线性回归模型。

• 线性回归 (linear regression)

一种回归模型，通过将输入特征进行线性组合输出连续值。

• 逻辑回归 (logistic regression)

一种模型，通过将 S 型函数应用于线性预测，生成分类问题中每个可能的离散标签值的概率。虽然逻辑回归经常用于二元分类问题，但也可用于多类别分类问题（其叫法变为多类别逻辑回归或多项回归）。

• 对数 (logits)

分类模型生成的原始（非标准化）预测向量，通常会传递给标准化函数。如果模型要解决多类别分类问题，则对数通常变成 softmax 函数的输入。之后，softmax 函数会生成一个（标准化）概率向量，对应于每个可能的类别。

此外，对数有时也称为 S 型函数的元素级反函数。如需了解详细信息，请参阅 tf.nn.sigmoid_cross_entropy_with_logits。

• 对数损失函数 (Log Loss)

二元逻辑回归中使用的损失函数。

• 对数几率 (log-odds)

某个事件几率的对数。

如果事件涉及二元概率，则几率指的是成功概率 (p) 与失败概率 (1-p) 之比。例如，假设某个给定事件的成功概率为 90％，失败概率为 10％。在这种情况下，几率的计算公式如下：

简单来说，对数几率即几率的对数。按照惯例，“对数”指自然对数，但对数的基数其实可以是任何大于 1 的数。若遵循惯例，上述示例的对数几率应为：

对数几率是S 型函数的反函数。

• 损失 (Loss)

一种衡量指标，用于衡量模型的预测偏离其标签的程度。或者更悲观地说是衡量模型有多差。要确定此值，模型必须定义损失函数。例如，线性回归模型通常将均方误差用作损失函数，而逻辑回归模型则使用对数损失函数。

---

M

• 机器学习 (machine learning)

一种程序或系统，用于根据输入数据构建（训练）预测模型。这种系统会利用学到的模型根据从分布（训练该模型时使用的同一分布）中提取的新数据（以前从未见过的数据）进行实用的预测。机器学习还指与这些程序或系统相关的研究领域。

• 均方误差 (MSE, Mean Squared Error)

每个样本的平均平方损失。MSE 的计算方法是平方损失除以样本数。TensorFlow Playground 显示的“训练损失”值和“测试损失”值都是 MSE。

• 指标 (metric)

您关心的一个数值。可能可以也可能不可以直接在机器学习系统中得到优化。您的系统尝试优化的指标称为目标。

• Metrics API (tf.metrics)

一种用于评估模型的 TensorFlow API。例如，tf.metrics.accuracy 用于确定模型的预测与标签匹配的频率。在编写自定义 Estimator 时，您可以调用 Metrics API 函数来指定应如何评估您的模型。

• 小批次 (mini-batch)

从整批样本内随机选择并在训练或推断过程的一次迭代中一起运行的一小部分样本。小批次的批次大小通常介于 10 到 1000 之间。与基于完整的训练数据计算损失相比，基于小批次数据计算损失要高效得多。

• 小批次随机梯度下降法 (SGD, mini-batch stochastic gradient descent)

一种采用小批次样本的梯度下降法。也就是说，小批次 SGD 会根据一小部分训练数据来估算梯度。Vanilla SGD 使用的小批次的大小为 1。

• ML

机器学习的缩写。

• 模型 (model)

机器学习系统从训练数据学到的内容的表示形式。多含义术语，可以理解为下列两种相关含义之一：

• 一种 TensorFlow 图，用于表示预测的计算结构。

• 该 TensorFlow 图的特定权重和偏差，通过训练决定。

• 模型函数 (model function)

Estimator 中的函数，用于实现机器学习训练、评估和推断。例如，模型函数的训练部分可以处理以下任务：定义深度神经网络的拓扑并确定其优化器函数。如果使用预创建的 Estimator，则有人已为您编写了模型函数。如果使用自定义 Estimator，则必须自行编写模型函数。

有关编写模型函数的详细信息，请参阅创建自定义 Estimator。

• 模型训练 (model training)

确定最佳模型的过程。

• 动量 (Momentum)

一种先进的梯度下降法，其中学习步长不仅取决于当前步长的导数，还取决于之前一步或多步的步长的导数。动量涉及计算梯度随时间而变化的指数级加权移动平均值，与物理学中的动量类似。动量有时可以防止学习过程被卡在局部最小的情况。

• 多类别分类 (multi-class classification)

区分两种以上类别的分类问题。例如，枫树大约有 128 种，因此，确定枫树种类的模型就属于多类别模型。反之，仅将电子邮件分为两类（“垃圾邮件”和“非垃圾邮件”）的模型属于二元分类模型。

• 多项分类 (multinomial classification)

与多类别分类的含义相同。

N

• NaN 陷阱 (NaN trap)

模型中的一个数字在训练期间变成 NaN，这会导致模型中的很多或所有其他数字最终也会变成 NaN。

NaN 是“非数字”的缩写。

• 负类别 (negative class)

在二元分类中，一种类别称为正类别，另一种类别称为负类别。正类别是我们要寻找的类别，负类别则是另一种可能性。例如，在医学检查中，负类别可以是“非肿瘤”。在电子邮件分类器中，负类别可以是“非垃圾邮件”。另请参阅正类别。

• 神经网络 (neural network)

一种模型，灵感来源于脑部结构，由多个层构成（至少有一个是隐藏层），每个层都包含简单相连的单元或神经元（具有非线性关系）。

• 神经元 (neuron)

神经网络中的节点，通常会接收多个输入值并生成一个输出值。神经元通过将激活函数（非线性转换）应用于输入值的加权和来计算输出值。

• 节点 (node)

多含义术语，可以理解为下列两种含义之一：

• 隐藏层中的神经元。

• TensorFlow 图中的操作。

• 标准化 (normalization)

将实际的值区间转换为标准的值区间（通常为 -1 到 +1 或 0 到 1）的过程。例如，假设某个特征的自然区间是 800 到 6000。通过减法和除法运算，您可以将这些值标准化为位于 -1 到 +1 区间内。

另请参阅缩放。

• 数值数据 (numerical data)

用整数或实数表示的特征。例如，在房地产模型中，您可能会用数值数据表示房子大小（以平方英尺或平方米为单位）。如果用数值数据表示特征，则可以表明特征的值相互之间具有数学关系，并且与标签可能也有数学关系。例如，如果用数值数据表示房子大小，则可以表明面积为 200 平方米的房子是面积为 100 平方米的房子的两倍。此外，房子面积的平方米数可能与房价存在一定的数学关系。

并非所有整数数据都应表示成数值数据。例如，世界上某些地区的邮政编码是整数，但在模型中，不应将整数邮政编码表示成数值数据。这是因为邮政编码 20000 在效力上并不是邮政编码 10000 的两倍（或一半）。此外，虽然不同的邮政编码确实与不同的房地产价值有关，但我们也不能假设邮政编码为 20000 的房地产在价值上是邮政编码为 10000 的房地产的两倍。邮政编码应表示成分类数据。

数值特征有时称为连续特征。

• Numpy

一个开放源代码数学库，在 Python 中提供高效的数组操作。Pandas 建立在 Numpy 之上。

---

O

• 目标 (objective)

算法尝试优化的指标。

• 离线推断 (offline inference)

生成一组预测，存储这些预测，然后根据需求检索这些预测。与在线推断相对。

• 独热编码 (one-hot encoding)

一种稀疏向量，其中：

• 一个元素设为 1。

• 所有其他元素均设为 0。

独热编码常用于表示拥有有限个可能值的字符串或标识符。例如，假设某个指定的植物学数据集记录了 15000 个不同的物种，其中每个物种都用独一无二的字符串标识符来表示。在特征工程过程中，您可能需要将这些字符串标识符编码为独热向量，向量的大小为 15000。

• 单样本学习（one-shot learning，通常用于对象分类）

一种机器学习方法，通常用于对象分类，旨在通过单个训练样本学习有效的分类器。

另请参阅少量样本学习。

• 一对多 (one-vs.-all)

假设某个分类问题有 N 种可能的解决方案，一对多解决方案将包含 N 个单独的二元分类器 - 一个二元分类器对应一种可能的结果。例如，假设某个模型用于区分样本属于动物、蔬菜还是矿物，一对多解决方案将提供下列三个单独的二元分类器：

• 动物和非动物

• 蔬菜和非蔬菜

• 矿物和非矿物

• 在线推断 (online inference)

根据需求生成预测。与离线推断相对。

• 操作 (op, Operation)

TensorFlow 图中的节点。在 TensorFlow 中，任何创建、操纵或销毁张量的过程都属于操作。例如，矩阵相乘就是一种操作，该操作以两个张量作为输入，并生成一个张量作为输出。

• 优化器 (optimizer)

梯度下降法的一种具体实现。TensorFlow 的优化器基类是 tf.train.Optimizer。不同的优化器可能会利用以下一个或多个概念来增强梯度下降法在指定训练集中的效果：

• 动量 (Momentum)

• 更新频率（AdaGrad = ADAptive GRADient descent；Adam = ADAptive with Momentum；RMSProp）

• 稀疏性/正则化 (Ftrl)

• 更复杂的数学方法（Proximal，等等）

甚至还包括 NN 驱动的优化器。

• 离群值 (outlier)

与大多数其他值差别很大的值。在机器学习中，下列所有值都是离群值。

• 绝对值很高的权重。

• 与实际值相差很大的预测值。

• 值比平均值高大约 3 个标准偏差的输入数据。

离群值常常会导致模型训练出现问题。

• 输出层 (output layer)

神经网络的“最后”一层，也是包含答案的层。

• 过拟合 (overfitting)

创建的模型与训练数据过于匹配，以致于模型无法根据新数据做出正确的预测。

---

P

• Pandas

面向列的数据分析 API。很多机器学习框架（包括 TensorFlow）都支持将 Pandas 数据结构作为输入。请参阅 Pandas 文档。

• 参数 (parameter)

机器学习系统自行训练的模型的变量。例如，权重就是一种参数，它们的值是机器学习系统通过连续的训练迭代逐渐学习到的。与超参数相对。

• 参数服务器 (PS, Parameter Server)

一种作业，负责在分布式设置中跟踪模型参数。

• 参数更新 (parameter update)

在训练期间（通常是在梯度下降法的单次迭代中）调整模型参数的操作。

• 偏导数 (partial derivative)

一种导数，除一个变量之外的所有变量都被视为常量。例如，f(x, y) 对 x 的偏导数就是 f(x) 的导数（即，使 y 保持恒定）。f 对 x 的偏导数仅关注 x 如何变化，而忽略公式中的所有其他变量。

• 划分策略 (partitioning strategy)

在参数服务器间分割变量的算法。

• 性能 (performance)

多含义术语，具有以下含义：

• 在软件工程中的传统含义。即：相应软件的运行速度有多快（或有多高效）？

• 在机器学习中的含义。在机器学习领域，性能旨在回答以下问题：相应模型的准确度有多高？即模型在预测方面的表现有多好？

• 困惑度 (perplexity)

一种衡量指标，用于衡量模型能够多好地完成任务。例如，假设任务是读取用户使用智能手机键盘输入字词时输入的前几个字母，然后列出一组可能的完整字词。此任务的困惑度 (P) 是：为了使列出的字词中包含用户尝试输入的实际字词，您需要提供的猜测项的个数。

困惑度与交叉熵的关系如下：

• 流水线 (pipeline)

机器学习算法的基础架构。流水线包括收集数据、将数据放入训练数据文件、训练一个或多个模型，以及将模型导出到生产环境。

池化 (pooling)

将一个或多个由前趋的**卷积层**创建的矩阵压缩为较小的矩阵。池化通常是取整个池化区域的最大值或平均值。以下面的 3x3 矩阵为例：

池化运算与卷积运算类似：将矩阵分割为多个切片，然后按步长逐个运行卷积运算。例如，假设池化运算按 1x1 步长将卷积矩阵分割为 2x2 个切片。如下图所示，进行了四个池化运算。假设每个池化运算都选择该切片中四个值的最大值：

池化有助于在输入矩阵中实现平移不变性。

对于视觉应用来说，池化的更正式名称为空间池化。时间序列应用通常将池化称为时序池化。按照不太正式的说法，池化通常称为下采样或降采样。

• 正类别 (positive class)

在二元分类中，两种可能的类别分别被标记为正类别和负类别。正类别结果是我们要测试的对象。（不可否认的是，我们会同时测试这两种结果，但只关注正类别结果。）例如，在医学检查中，正类别可以是“肿瘤”。在电子邮件分类器中，正类别可以是“垃圾邮件”。

与负类别相对。

• 精确率 (precision)

一种分类模型指标。精确率指模型正确预测正类别的频率，即：

精确率正例数正例数假正例数

• 预测 (prediction)

模型在收到输入样本后的输出。

• 预测偏差 (prediction bias)

一种值，用于表明预测平均值与数据集中标签的平均值相差有多大。

• 预创建的 Estimator (pre-made Estimator)

其他人已建好的 Estimator。TensorFlow 提供了一些预创建的 Estimator，包括 DNNClassifier、DNNRegressor 和 LinearClassifier。您可以按照这些说明构建自己预创建的 Estimator。

• 预训练模型 (pre-trained model)

已经过训练的模型或模型组件（例如嵌套）。有时，您需要将预训练的嵌套馈送到神经网络。在其他时候，您的模型将自行训练嵌套，而不依赖于预训练的嵌套。

• 先验信念 (prior belief)

在开始采用相应数据进行训练之前，您对这些数据抱有的信念。例如，L2 正则化依赖的先验信念是权重应该很小且应以 0 为中心呈正态分布。

---

Q

• 队列 (queue)

一种 TensorFlow 操作，用于实现队列数据结构。通常用于 I/O 中。

---

R

• 等级 (rank)

机器学习中的一个多含义术语，可以理解为下列含义之一：

• 张量中的维数。例如，标量等级为 0，向量等级为 1，矩阵等级为 2。

• 在将类别从最高到最低进行排序的机器学习问题中，类别的顺序位置。例如，行为排序系统可以将狗狗的奖励从最高（牛排）到最低（枯萎的羽衣甘蓝）进行排序。

• 评分者 (rater)

为样本提供标签的人。有时称为“注释者”。

• 召回率 (recall)

一种分类模型指标，用于回答以下问题：在所有可能的正类别标签中，模型正确地识别出了多少个？即：

• 修正线性单元 (ReLU, Rectified Linear Unit)

一种激活函数，其规则如下：

• 如果输入为负数或 0，则输出 0。

• 如果输入为正数，则输出等于输入。

• 回归模型 (regression model)

一种模型，能够输出连续的值（通常为浮点值）。请与分类模型进行比较，分类模型会输出离散值，例如“黄花菜”或“虎皮百合”。

• 正则化 (regularization)

对模型复杂度的惩罚。正则化有助于防止出现过拟合，包含以下类型：

• L1 正则化

• L2 正则化

• 丢弃正则化

• 早停法（这不是正式的正则化方法，但可以有效限制过拟合）

• 正则化率 (regularization rate)

一种标量值，以 lambda 表示，用于指定正则化函数的相对重要性。从下面简化的损失公式中可以看出正则化率的影响：

最小化损失方程正则化方程

提高正则化率可以减少过拟合，但可能会使模型的准确率降低。

• 表示法 (representation)

将数据映射到实用特征的过程。

• 受试者工作特征曲线（receiver operating characteristic，简称 ROC 曲线）

不同分类阈值下的正例率和假正例率构成的曲线。另请参阅曲线下面积。

• 根目录 (root directory)

您指定的目录，用于托管多个模型的 TensorFlow 检查点和事件文件的子目录。

• 均方根误差 (RMSE, Root Mean Squared Error)

均方误差的平方根。

• 旋转不变性 (rotational invariance)

在图像分类问题中，即使图像的方向发生变化，算法也能成功地对图像进行分类。例如，无论网球拍朝上、侧向还是朝下放置，该算法仍然可以识别它。请注意，并非总是希望旋转不变；例如，倒置的“9”不应分类为“9”。

另请参阅平移不变性和大小不变性。

---

S

• SavedModel

保存和恢复 TensorFlow 模型时建议使用的格式。SavedModel 是一种独立于语言且可恢复的序列化格式，使较高级别的系统和工具可以创建、使用和转换 TensorFlow 模型。

如需完整的详细信息，请参阅《TensorFlow 编程人员指南》中的保存和恢复。

• Saver

一种 TensorFlow 对象，负责保存模型检查点。

• 缩放 (scaling)

特征工程中的一种常用做法，是指对某个特征的值区间进行调整，使之与数据集中其他特征的值区间一致。例如，假设您希望数据集中所有浮点特征的值都位于 0 到 1 区间内，如果某个特征的值位于 0 到 500 区间内，您就可以通过将每个值除以 500 来缩放该特征。

另请参阅标准化。

• scikit-learn

一个热门的开放源代码机器学习平台。请访问 www.scikit-learn.org。

• 半监督式学习 (semi-supervised learning)

训练模型时采用的数据中，某些训练样本有标签，而其他样本则没有标签。半监督式学习采用的一种技术是推断无标签样本的标签，然后使用推断出的标签进行训练，以创建新模型。如果获得有标签样本需要高昂的成本，而无标签样本则有很多，那么半监督式学习将非常有用。

• 序列模型 (sequence model)

一种模型，其输入具有序列依赖性。例如，根据之前观看过的一系列视频对观看的下一个视频进行预测。

• 会话 (tf.session)

封装了 TensorFlow 运行时状态的对象，用于运行全部或部分**图**。在使用底层 TensorFlow API 时，您可以直接创建并管理一个或多个 tf.session 对象。在使用 Estimator API 时，Estimator 会为您创建会话对象。

• S 型函数 (sigmoid function)

一种函数，可将逻辑回归输出或多项回归输出（对数几率）映射到概率，以返回介于 0 到 1 之间的值。S 型函数的公式如下：

在逻辑回归问题中， 非常简单：

换句话说，S 型函数可将转换为介于 0 到 1 之间的概率。

在某些神经网络中，S 型函数可作为激活函数使用。

• 大小不变性 (size invariance)

在图像分类问题中，即使图像的大小发生变化，算法也能成功地对图像进行分类。例如，无论一只猫以 200 万像素还是 20 万像素呈现，该算法仍然可以识别它。请注意，即使是最好的图像分类算法，在大小不变性方面仍然会存在切实的限制。例如，对于仅以 20 像素呈现的猫图像，算法（或人）不可能正确对其进行分类。

另请参阅平移不变性和旋转不变性。

• softmax

一种函数，可提供多类别分类模型中每个可能类别的概率。这些概率的总和正好为 1.0。例如，softmax 可能会得出某个图像是狗、猫和马的概率分别是 0.9、0.08 和 0.02。（也称为完整 softmax。）

与候选采样相对。

• 稀疏特征 (sparse feature)

一种特征向量，其中的大多数值都为 0 或为空。例如，某个向量包含一个为 1 的值和一百万个为 0 的值，则该向量就属于稀疏向量。再举一个例子，搜索查询中的单词也可能属于稀疏特征 - 在某种指定语言中有很多可能的单词，但在某个指定的查询中仅包含其中几个。

与密集特征相对。

• 稀疏表示法 (sparse representation)

一种张量表示法，仅存储非零元素。

例如，英语中包含约一百万个单词。表示一个英语句子中所用单词的数量，考虑以下两种方式：

• 要采用密集表示法来表示此句子，则必须为所有一百万个单元格设置一个整数，然后在大部分单元格中放入 0，在少数单元格中放入一个非常小的整数。

• 要采用稀疏表示法来表示此句子，则仅存储象征句子中实际存在的单词的单元格。因此，如果句子只包含 20 个独一无二的单词，那么该句子的稀疏表示法将仅在 20 个单元格中存储一个整数。

例如，假设以两种方式来表示句子“Dogs wag tails.”。如下表所示，密集表示法将使用约一百万个单元格；稀疏表示法则只使用 3 个单元格：

• 稀疏性 (sparsity)

向量或矩阵中设置为 0（或空）的元素数除以该向量或矩阵中的条目总数。以一个 10x10 矩阵（其中 98 个单元格都包含 0）为例。稀疏性的计算方法如下：

特征稀疏性是指特征向量的稀疏性；模型稀疏性是指模型权重的稀疏性。

• 空间池化 (spatial pooling)

请参阅池化。

• 平方合页损失函数 (squared hinge loss)

合页损失函数的平方。与常规合页损失函数相比，平方合页损失函数对离群值的惩罚更严厉。

• 平方损失函数 (squared loss)

在线性回归中使用的损失函数（也称为 L2 损失函数）。该函数可计算模型为有标签样本预测的值和标签的实际值之差的平方。由于取平方值，因此该损失函数会放大不佳预测的影响。也就是说，与 L1 损失函数相比，平方损失函数对离群值的反应更强烈。

• 静态模型 (static model)

离线训练的一种模型。

• 平稳性 (stationarity)

数据集中数据的一种属性，表示数据分布在一个或多个维度保持不变。这种维度最常见的是时间，即表明平稳性的数据不随时间而变化。例如，从 9 月到 12 月，表明平稳性的数据没有发生变化。

• 步 (step)

对一个批次的向前和向后评估。

• 步长 (step size)

与学习速率的含义相同。

• 随机梯度下降法 (SGD, stochastic gradient descent)

批次大小为 1 的一种梯度下降法。换句话说，SGD 依赖于从数据集中随机均匀选择的单个样本来计算每步的梯度估算值。

• 结构风险最小化 (SRM, structural risk minimization)

一种算法，用于平衡以下两个目标：

• 期望构建最具预测性的模型（例如损失最低）。

• 期望使模型尽可能简单（例如强大的正则化）。

例如，旨在将基于训练集的损失和正则化降至最低的函数就是一种结构风险最小化算法。

如需更多信息，请参阅 http://www.svms.org/srm/。

与经验风险最小化相对。

• 步长 (stride)

在卷积运算或池化中，下一个系列的输入切片的每个维度中的增量。例如，下面的动画演示了卷积运算过程中的一个 (1,1) 步长。因此，下一个输入切片是从上一个输入切片向右移动一个步长的位置开始。当运算到达右侧边缘时，下一个切片将回到最左边，但是下移一个位置。

前面的示例演示了一个二维步长。如果输入矩阵为三维，那么步长也将是三维。

• 下采样 (subsampling)

请参阅池化。

• 总结 (summary)

在 TensorFlow 中的某一步计算出的一个值或一组值，通常用于在训练期间跟踪模型指标。

• 监督式机器学习 (supervised machine learning)

根据输入数据及其对应的标签来训练模型。监督式机器学习类似于学生通过研究一系列问题及其对应的答案来学习某个主题。在掌握了问题和答案之间的对应关系后，学生便可以回答关于同一主题的新问题（以前从未见过的问题）。请与非监督式机器学习进行比较。

• 合成特征 (synthetic feature)

一种特征，不在输入特征之列，而是从一个或多个输入特征衍生而来。合成特征包括以下类型：

• 对连续特征进行分桶，以分为多个区间分箱。

• 将一个特征值与其他特征值或其本身相乘（或相除）。

• 创建一个特征组合。

仅通过标准化或缩放创建的特征不属于合成特征。

---

T

• 目标 (target)

与标签的含义相同。

• 时态数据 (temporal data)

在不同时间点记录的数据。例如，记录的一年中每一天的冬外套销量就属于时态数据。

• 张量 (Tensor)

TensorFlow 程序中的主要数据结构。张量是 N 维（其中 N 可能非常大）数据结构，最常见的是标量、向量或矩阵。张量的元素可以包含整数值、浮点值或字符串值。

• 张量处理单元 (TPU, Tensor Processing Unit)

一种 ASIC（应用专用集成电路），用于优化 TensorFlow 程序的性能。

• 张量等级 (Tensor rank)

请参阅等级。

• 张量形状 (Tensor shape)

张量在各种维度中包含的元素数。例如，张量 [5, 10] 在一个维度中的形状为 5，在另一个维度中的形状为 10。

• 张量大小 (Tensor size)

张量包含的标量总数。例如，张量 [5, 10] 的大小为 50。

• TensorBoard

一个信息中心，用于显示在执行一个或多个 TensorFlow 程序期间保存的摘要信息。

• TensorFlow

一个大型的分布式机器学习平台。该术语还指 TensorFlow 堆栈中的基本 API 层，该层支持对数据流图进行一般计算。

虽然 TensorFlow 主要应用于机器学习领域，但也可用于需要使用数据流图进行数值计算的非机器学习任务。

• TensorFlow Playground

一款用于直观呈现不同的超参数对模型（主要是神经网络）训练的影响的程序。要试用 TensorFlow Playground，请前往 http://playground.tensorflow.org。

• TensorFlow Serving

一个平台，用于将训练过的模型部署到生产环境。

• 测试集 (test set)

数据集的子集，用于在模型经由验证集的初步验证之后测试模型。

与训练集和验证集相对。

• tf.Example

一种标准协议缓冲区，旨在描述用于机器学习模型训练或推断的输入数据。

• 时间序列分析 (time series analysis)

机器学习和统计学的一个子领域，旨在分析时态数据。很多类型的机器学习问题都需要时间序列分析，其中包括分类、聚类、预测和异常检测。例如，您可以利用时间序列分析根据历史销量数据预测未来每月的冬外套销量。

• 训练 (training)

确定构成模型的理想参数的过程。

• 训练集 (training set)

数据集的子集，用于训练模型。

与验证集和测试集相对。

• 迁移学习 (transfer learning)

将信息从一个机器学习任务迁移到另一个机器学习任务。例如，在多任务学习中，一个模型可以完成多项任务，例如针对不同任务具有不同输出节点的深度模型。迁移学习可能涉及将知识从较简单任务的解决方案迁移到较复杂的任务，或者将知识从数据较多的任务迁移到数据较少的任务。

大多数机器学习系统都只能完成一项任务。迁移学习是迈向人工智能的一小步；在人工智能中，单个程序可以完成多项任务。

• 平移不变性 (translational invariance)

在图像分类问题中，即使图像中对象的位置发生变化，算法也能成功对图像进行分类。例如，无论一只狗位于画面正中央还是画面左侧，该算法仍然可以识别它。

另请参阅大小不变性和旋转不变性。

• 负例 (TN, true negative)

被模型正确地预测为负类别的样本。例如，模型推断出某封电子邮件不是垃圾邮件，而该电子邮件确实不是垃圾邮件。

• 正例 (TP, true positive)

被模型正确地预测为正类别的样本。例如，模型推断出某封电子邮件是垃圾邮件，而该电子邮件确实是垃圾邮件。

• 正例率（true positive rate, 简称 TP 率）

与召回率的含义相同，即：

正例率正例数正例数假负例数

正例率是 ROC 曲线的 y 轴。

---

U

• 无标签样本 (unlabeled example)

包含特征但没有标签的样本。无标签样本是用于进行推断的输入内容。在半监督式和非监督式学习中，在训练期间会使用无标签样本。

• 非监督式机器学习 (unsupervised machine learning)

训练模型，以找出数据集（通常是无标签数据集）中的规律。

非监督式机器学习最常见的用途是将数据分为不同的聚类，使相似的样本位于同一组中。例如，非监督式机器学习算法可以根据音乐的各种属性将歌曲分为不同的聚类。

所得聚类可以作为其他机器学习算法（例如音乐推荐服务）的输入。在很难获取真标签的领域，聚类可能会非常有用。例如，在反滥用和反欺诈等领域，聚类有助于人们更好地了解相关数据。

非监督式机器学习的另一个例子是主成分分析 (PCA)。例如，通过对包含数百万购物车中物品的数据集进行主成分分析，可能会发现有柠檬的购物车中往往也有抗酸药。

请与监督式机器学习进行比较。

---

V

• 验证集 (validation set)

数据集的一个子集，从训练集分离而来，用于调整超参数。

与训练集和测试集相对。

---

W

• 权重 (weight)

线性模型中特征的系数，或深度网络中的边。训练线性模型的目标是确定每个特征的理想权重。如果权重为 0，则相应的特征对模型来说没有任何贡献。

• 宽度模型 (wide model)

一种线性模型，通常有很多稀疏输入特征。我们之所以称之为“宽度模型”，是因为这是一种特殊类型的神经网络，其大量输入均直接与输出节点相连。与深度模型相比，宽度模型通常更易于调试和检查。虽然宽度模型无法通过隐藏层来表示非线性关系，但可以利用特征组合、分桶等转换以不同的方式为非线性关系建模。

与深度模型相对。

算法原理 

1. 什么是机器学习？

机器通过分析大量数据来进行学习。比如说，不需要通过编程来识别猫或人脸，它们可以通过使用图片来进行训练，从而归纳和识别特定的目标。

机器学习和人工智能的关系

机器学习是一种重在寻找数据中的模式并使用这些模式来做出预测的研究和算法的门类。机器学习是人工智能领域的一部分，并且和知识发现与数据挖掘有所交集。

机器学习的工作方式

①选择数据：将你的数据分成三组：训练数据、验证数据和测试数据；

②模型数据：使用训练数据来构建使用相关特征的模型；

③验证模型：使用你的验证数据接入你的模型；

④测试模型：使用你的测试数据检查被验证的模型的表现；

⑤使用模型：使用完全训练好的模型在新数据上做预测；

⑥调优模型：使用更多数据、不同的特征或调整过的参数来提升算法的性能表现。

机器学习所处的位置

①传统编程：软件工程师编写程序来解决问题。首先存在一些数据→为了解决一个问题，软件工程师编写一个流程来告诉机器应该怎样做→计算机遵照这一流程执行，然后得出结果；

②统计学：分析师比较变量之间的关系；

③机器学习：数据科学家使用训练数据集来教计算机应该怎么做，然后系统执行该任务。首先存在大数据→机器会学习使用训练数据集来进行分类，调节特定的算法来实现目标分类→该计算机可学习识别数据中的关系、趋势和模式；

④智能应用：智能应用使用人工智能所得到的结果，如图是一个精准农业的应用案例示意，该应用基于无人机所收集到的数据。

机器学习的实际应用

机器学习有很多应用场景，这里给出了一些示例，你会怎么使用它？

• 快速三维地图测绘和建模：要建造一架铁路桥，PwC 的数据科学家和领域专家将机器学习应用到了无人机收集到的数据上。这种组合实现了工作成功中的精准监控和快速反馈。

• 增强分析以降低风险：为了检测内部交易，PwC 将机器学习和其它分析技术结合了起来，从而开发了更为全面的用户概况，并且获得了对复杂可疑行为的更深度了解。

• 预测表现最佳的目标：PwC 使用机器学习和其它分析方法来评估 Melbourne Cup 赛场上不同赛马的潜力。

机器学习的算法

1. 决策树（Decision Tree）：在进行逐步应答过程中，典型的决策树分析会使用分层变量或决策节点，例如，可将一个给定用户分类成信用可靠或不可靠。

• 优点：擅长对人、地点、事物的一系列不同特征、品质、特性进行评估；

• 场景举例：基于规则的信用评估、赛马结果预测。

  

  2. 支持向量机（Support Vector Machine）：基于超平面（hyperplane），支持向量机可以对数据群进行分类。

  3. 回归（Regression）：回归可以勾画出因变量与一个或多个因变量之间的状态关系。在这个例子中，将垃圾邮件和非垃圾邮件进行了区分。

  

  4. 朴素贝叶斯分类（Naive Bayes Classification）：朴素贝叶斯分类器用于计算可能条件的分支概率。

  每个独立的特征都是「朴素」或条件独立的，因此它们不会影响别的对象。例如，在一个装有共 5 个黄色和红色小球的罐子里，连续拿到两个黄色小球的概率是多少？从图中最上方分支可见，前后抓取两个黄色小球的概率为 1/10。朴素贝叶斯分类器可以计算多个特征的联合条件概率。

  5. 隐马尔可夫模型（Hidden Markov model）：显马尔可夫过程是完全确定性的——一个给定的状态经常会伴随另一个状态。

  交通信号灯就是一个例子。相反，隐马尔可夫模型通过分析可见数据来计算隐藏状态的发生。随后，借助隐藏状态分析，隐马尔可夫模型可以估计可能的未来观察模式。在本例中，高或低气压的概率（这是隐藏状态）可用于预测晴天、雨天、多云天的概率。

  

  6. 随机森林（Random forest）：随机森林算法通过使用多个带有随机选取的数据子集的树（tree）改善了决策树的精确性。

  本例在基因表达层面上考察了大量与乳腺癌复发相关的基因，并计算出复发风险。

  7. 循环神经网络（Recurrent neural network）：在任意神经网络中，每个神经元都通过 1 个或多个隐藏层来将很多输入转换成单个输出。

  循环神经网络（RNN）会将值进一步逐层传递，让逐层学习成为可能。换句话说，RNN 存在某种形式的记忆，允许先前的输出去影响后面的输入。

  8. 长短期记忆（Long short-term memory，LSTM）与门控循环单元神经网络（gated recurrent unit nerual network）：早期的 RNN 形式是会存在损耗的。

  尽管这些早期循环神经网络只允许留存少量的早期信息，新近的长短期记忆（LSTM）与门控循环单元（GRU）神经网络都有长期与短期的记忆。换句话说，这些新近的 RNN 拥有更好的控制记忆的能力，允许保留早先的值或是当有必要处理很多系列步骤时重置这些值，这避免了「梯度衰减」或逐层传递的值的最终 degradation。LSTM 与 GRU 网络使得我们可以使用被称为「门（gate）」的记忆模块或结构来控制记忆，这种门可以在合适的时候传递或重置值。

  9. 卷积神经网络（convolutional neural network）：卷积是指来自后续层的权重的融合，可用于标记输出层。

  • 优点：当存在非常大型的数据集、大量特征和复杂的分类任务时，卷积神经网络是非常有用的；

  • 场景举例：图像识别、文本转语音、药物发现。

  • 优点：长短期记忆和门控循环单元神经网络具备与其它循环神经网络一样的优点，但因为它们有更好的记忆能力，所以更常被使用；

  • 场景举例：自然语言处理、翻译。

  • 优点：循环神经网络在存在大量有序信息时具有预测能力；

  • 场景举例：图像分类与字幕添加、政治情感分析。

  • 优点：随机森林方法被证明对大规模数据集和存在大量且有时不相关特征的项（item）来说很有用；

  • 场景举例：用户流失分析、风险评估。

  • 优点：容许数据的变化性，适用于识别（recognition）和预测操作；

  • 场景举例：面部表情分析、气象预测。

  • 优点：对于在小数据集上有显著特征的相关对象，朴素贝叶斯方法可对其进行快速分类；

  • 场景举例：情感分析、消费者分类。

  • 优点：回归可用于识别变量之间的连续关系，即便这个关系不是非常明显；

  • 场景举例：路面交通流量分析、邮件过滤。

  • 优点：支持向量机擅长在变量 X 与其它变量之间进行二元分类操作，无论其关系是否是线性的；

  • 场景举例：新闻分类、手写识别。

机器学习的组成

抛开所有和人工智能(AI)有关的扯淡成分，机器学习唯一的目标是基于输入的数据来预测结果，就这样。所有的机器学习任务都可以用这种方式来表示，否则从一开始它就不是个机器学习问题。

样本越是多样化，越容易找到相关联的模式以及预测出结果。因此，我们需要3个部分来训练机器：

（1）数据

想检测垃圾邮件？获取垃圾信息的样本。想预测股票？找到历史价格信息。想找出用户偏好？分析他们在Facebook上的活动记录(不，Mark，停止收集数据~已经够了)。数据越多样化，结果越好。对于拼命运转的机器而言，至少也得几十万行数据才够吧。

获取数据有两种主要途径——手动或者自动。手动采集的数据混杂的错误少，但要耗费更多的时间——通常花费也更多。自动化的方法相对便宜，你可以搜集一切能找到的数据(但愿数据质量够好)。

一些像Google这样聪明的家伙利用自己的用户来为他们免费标注数据，还记得ReCaptcha(人机验证)强制你去“选择所有的路标”么？他们就是这样获取数据的，还是免费劳动！干得漂亮。如果我是他们，我会更频繁地展示这些验证图片，不过，等等……

好的数据集真的很难获取，它们是如此重要，以至于有的公司甚至可能开放自己的算法，但很少公布数据集。

（2）特征

也可以称为“参数”或者“变量”，比如汽车行驶公里数、用户性别、股票价格、文档中的词频等。换句话说，这些都是机器需要考虑的因素。如果数据是以表格的形式存储，特征就对应着列名，这种情形比较简单。但如果是100GB的猫的图片呢？我们不能把每个像素都当做特征。这就是为什么选择适当的特征通常比机器学习的其他步骤花更多时间的原因，特征选择也是误差的主要来源。人性中的主观倾向，会让人去选择自己喜欢或者感觉“更重要”的特征——这是需要避免的。

（3）算法

最显而易见的部分。任何问题都可以用不同的方式解决。你选择的方法会影响到最终模型的准确性、性能以及大小。需要注意一点：如果数据质量差，即使采用最好的算法也无济于事。这被称为“垃圾进，垃圾出”(garbage in - garbage out,GIGO)。所以，在把大量心思花到正确率之前，应该获取更多的数据。

学习 V.S. 智能

下图展示了几个容易混淆的概念之间的关系。

“人工智能”是整个学科的名称，类似于“生物学”或“化学”。

“机器学习”是“人工智能”的重要组成部分，但不是唯一的部分。

“神经网络”是机器学习的一种分支方法，这种方法很受欢迎，不过机器学习大家庭下还有其他分支。

“深度学习”是关于构建、训练和使用神经网络的一种现代方法。本质上来讲，它是一种新的架构。在当前实践中，没人会将深度学习和“普通网络”区分开来，使用它们时需要调用的库也相同。为了不让自己看起来像个傻瓜，你最好直接说具体网络类型，避免使用流行语。

一般原则是在同一水平上比较事物。这就是为什么“神经网络将取代机器学习”听起来就像“车轮将取代汽车”。亲爱的媒体们，这会折损一大截你们的声誉哦。

机器学习世界的版图

如果你懒得阅读大段文字，下面这张图有助于获得一些认识。

在机器学习的世界里，解决问题的方法从来不是唯一的——记住这点很重要——因为你总会发现好几个算法都可以用来解决某个问题，你需要从中选择最适合的那个。当然，所有的问题都可以用“神经网络”来处理，但是背后承载算力的硬件成本谁来负担呢？

我们先从一些基础的概述开始。目前机器学习主要有4个方向。

分类算法

1.1 有监督学习

经典机器学习通常分为两类：有监督学习(Supervised Learning)和无监督学习(Unsupervised Learning)。

在“有监督学习”中，有一个“监督者”或者“老师”提供给机器所有的答案来辅助学习，比如图片中是猫还是狗。“老师”已经完成数据集的划分——标注“猫”或“狗”，机器就使用这些示例数据来学习，逐个学习区分猫或狗。

无监督学习就意味着机器在一堆动物图片中独自完成区分谁是谁的任务。数据没有事先标注，也没有“老师”，机器要自行找出所有可能的模式。后文再讨论这些。

很明显，有“老师”在场时，机器学的更快，因此现实生活中有监督学习更常用到。

有监督学习分为两类：

分类(classification)，预测一个对象所属的类别；

回归(regression)，预测数轴上的一个特定点；

分类(Classification)

“基于事先知道的一种属性来对物体划分类别，比如根据颜色来对袜子归类，根据语言对文档分类，根据风格来划分音乐。”

分类算法常用于：

过滤垃圾邮件；

语言检测；

查找相似文档；

情感分析

识别手写字母或数字

欺诈侦测

常用的算法：

朴素贝叶斯(Naive Bayes)

决策树(Decision Tree)

Logistic回归(Logistic Regression)

K近邻(K-Nearest Neighbours)

支持向量机(Support Vector Machine)

机器学习主要解决“分类”问题。这台机器好比在学习对玩具分类的婴儿一样：这是“机器人”，这是“汽车”，这是“机器-车”……额，等下，错误！错误！

在分类任务中，你需要一名“老师”。数据需要事先标注好，这样机器才能基于这些标签来学会归类。一切皆可分类——基于兴趣对用户分类，基于语言和主题对文章分类(这对搜索引擎很重要)，基于类型对音乐分类(Spotify播放列表)，你的邮件也不例外。

朴素贝叶斯算法广泛应用于垃圾邮件过滤。机器分别统计垃圾邮件和正常邮件中出现的“伟哥”等字样出现的频次，然后套用贝叶斯方程乘以各自的概率，再对结果求和——哈，机器就完成学习了。

后来，垃圾邮件制造者学会了如何应对贝叶斯过滤器——在邮件内容后面添加很多“好”词——这种方法被讽称为“贝叶斯中毒”(Bayesian poisoning)。朴素贝叶斯作为最优雅且是第一个实用的算法而载入历史，不过现在有其他算法来处理垃圾邮件过滤问题。

再举一个分类算法的例子。

假如现在你需要借一笔钱，那银行怎么知道你将来是否会还钱呢？没法确定。但是银行有很多历史借款人的档案，他们拥有诸如“年龄”、“受教育程度”、“职业”、“薪水”以及——最重要的——“是否还钱”这些数据。

利用这些数据，我们可以训练机器找到其中的模式并得出答案。找出答案并不成问题，问题在于银行不能盲目相信机器给出的答案。如果系统出现故障、遭遇黑客攻击或者喝高了的毕业生刚给系统打了个应急补丁，该怎么办？

要处理这个问题，我们需要用到决策树(Decision Trees)，所有数据自动划分为“是/否”式提问——比如“借款人收入是否超过128.12美元？”——听起来有点反人类。不过，机器生成这样的问题是为了在每个步骤中对数据进行最优划分。

“树”就是这样产生的。分支越高(接近根节点)，问题的范围就越广。所有分析师都能接受这种做法并在事后给出解释，即使他并不清楚算法是怎么回事，照样可以很容易地解释结果(典型的分析师啊)！

决策树广泛应用于高责任场景：诊断、医药以及金融领域。

最广为人知的两种决策树算法是 CART 和 C4.5.

如今，很少用到纯粹的决策树算法。不过，它们是大型系统的基石，决策树集成之后的效果甚至比神经网络还要好。这个我们后面再说。

当你在Google上搜索时，正是一堆笨拙的“树”在帮你寻找答案。搜索引擎喜欢这类算法，因为它们运行速度够快。

按理说，支持向量机(SVM) 应该是最流行的分类方法。只要是存在的事物都可以用它来分类：对图片中的植物按形状归类，对文档按类别归类等。

SVM背后的思想很简单——它试图在数据点之间绘制两条线，并尽可能最大化两条线之间的距离。

如下图示：

分类算法有一个非常有用的场景——异常检测(anomaly detection)，如果某个特征无法分配到所有类别上，我们就把它标出来。现在这种方法已经用于医学领域——MRI(磁共振成像)中，计算机会标记检测范围内所有的可疑区域或者偏差。股票市场使用它来检测交易人的异常行为以此来找到内鬼。在训练计算机分辨哪些事物是正确时，我们也自动教会其识别哪些事物是错误的。

经验法则(rule of thumb)表明，数据越复杂，算法就越复杂。对于文本、数字、表格这样的数据，我会选择经典方法来操作。这些模型较小，学习速度更快，工作流程也更清晰。对于图片、视频以及其他复杂的大数据，我肯定会研究神经网络。

就在5年前，你还可以找到基于SVM的人脸分类器。现在，从数百个预训练好的神经网络模型中挑选一个模型反而更容易。不过，垃圾邮件过滤器没什么变化，它们还是用SVM编写的，没什么理由去改变它。甚至我的网站也是用基于SVM来过滤评论中的垃圾信息的。

回归(Regression)

“画一条线穿过这些点，嗯~这就是机器学习”

回归算法目前用于：

股票价格预测

供应和销售量分析

医学诊断

计算时间序列相关性

常见的回归算法有：

线性回归（Linear Regression)

多项式回归(Polynomial Regression)

“回归”算法本质上也是“分类”算法，只不过预测的不是类别而是一个数值。比如根据行驶里程来预测车的价格，估算一天中不同时间的交通量，以及预测随着公司发展供应量的变化幅度等。处理和时间相关的任务时，回归算法可谓不二之选。

回归算法备受金融或者分析行业从业人员青睐。它甚至成了Excel的内置功能，整个过程十分顺畅——机器只是简单地尝试画出一条代表平均相关的线。不过，不同于一个拿着笔和白板的人，机器是通过计算每个点与线的平均间隔这样的数学精确度来完成的这件事。

如果画出来的是直线，那就是“线性回归”，如果线是弯曲的，则是“多项式回归”。它们是回归的两种主要类型。其他类型就比较少见了。不要被Logistics回归这个“害群之马”忽悠了，它是分类算法，不是回归。

不过，把“回归”和“分类”搞混也没关系。一些分类器调整参数后就变成回归了。除了定义对象的类别外，还要记住对象有多么的接近该类别，这就引出了回归问题。

如果你想深入研究，可以阅读奠基性教科书《深度学习》(强烈推荐)。

1.2 无监督学习

无监督学习比有监督学习出现得稍晚——在上世纪90年代，这类算法用的相对较少，有时候仅仅是因为没得选才找上它们。

有标注的数据是很奢侈的。假设现在我要创建一个——比如说“公共汽车分类器”，那我是不是要亲自去街上拍上几百万张该死的公共汽车的照片，然后还得把这些图片一一标注出来？没门，这会花费我毕生时间，我在Steam上还有很多游戏没玩呢。

这种情况下还是要对资本主义抱一点希望，得益于社会众包机制，我们可以得到数百万便宜的劳动力和服务。比如Mechanical Turk，背后是一群随时准备为了获得0.05美元报酬来帮你完成任务的人。事情通常就是这么搞定的。

或者，你可以尝试使用无监督学习。但是印象中，我不记得有什么关于它的最佳实践。无监督学习通常用于探索性数据分析(exploratory data analysis)，而不是作为主要的算法。

那些拥有牛津大学学位且经过特殊训练的人给机器投喂了一大堆垃圾然后开始观察：有没有聚类呢？没有。可以看到一些联系吗？没有。好吧，接下来，你还是想从事数据科学工作的，对吧？

聚类(Clustering)

“机器会选择最好的方式，基于一些未知的特征将事物区分开来。”

聚类算法目前用于：

市场细分(顾客类型，忠诚度)

合并地图上邻近的点

图像压缩

分析和标注新的数据

检测异常行为

常见算法：

K均值聚类

Mean-Shift

DBSCAN

聚类是在没有事先标注类别的前提下来进行类别划分。好比你记不住所有袜子的颜色时照样可以对袜子进行分类。聚类算法试图找出相似的事物(基于某些特征)，然后将它们聚集成簇。那些具有很多相似特征的对象聚在一起并划分到同一个类别。有的算法甚至支持设定每个簇中数据点的确切数量。

这里有个示范聚类的好例子——在线地图上的标记。当你寻找周围的素食餐厅时，聚类引擎将它们分组后用带数字的气泡展示出来。不这么做的话，浏览器会卡住——因为它试图将这个时尚都市里所有的300家素食餐厅绘制到地图上。

Apple Photos和Google Photos用的是更复杂的聚类方式。通过搜索照片中的人脸来创建你朋友们的相册。应用程序并不知道你有多少朋友以及他们的长相，但是仍可以从中找到共有的面部特征。这是很典型的聚类。

另一个常见的应用场景是图片压缩。当图片保存为PNG格式时，可以将色彩设置为32色。这就意味着聚类算法要找出所有的“红色”像素，然后计算出“平均红色”，再将这个均值赋给所有的红色像素点上。颜色更少，文件更小——划算！

但是，遇到诸如蓝绿这样的颜色时就麻烦了。这是绿色还是蓝色？此时就需要K-Means算法出场啦。

先随机从色彩中选出32个色点作为“簇心”，剩余的点按照最近的簇心进行标记。这样我们就得到了围绕着32个色点的“星团”。接着我们把簇心移动到“星团”的中心，然后重复上述步骤直到簇心不再移动为止。

完工。刚好聚成32个稳定的簇形。

给大家看一个现实生活中的例子：

寻找簇心这种方法很方便，不过，现实中的簇并不总是圆形的。假如你是一名地质学家，现在需要在地图上找出一些类似的矿石。这种情形下，簇的形状会很奇怪，甚至是嵌套的。甚至你都不知道会有多少个簇，10个？100个？

K-means算法在这里就派不上用场了，但是DBSCAN算法用得上。我们把数据点比作广场上的人，找到任何相互靠近的3个人请他们手拉手。接下来告诉他们抓住能够到的邻居的手(整个过程人的站立位置不能动)，重复这个步骤，直到新的邻居加入进来。这样我们就得到了第一个簇，重复上述过程直到每个人都被分配到簇，搞定。

一个意外收获：一个没有人牵手的人——异常数据点。

整个过程看起来很酷。

有兴趣继续了解基于位置数据的聚类算法可以阅读《位置数据的智能聚类算法研究》

就像分类算法一样，聚类可以用来检测异常。用户登陆之后的有不正常的操作？让机器暂时禁用他的账户，然后创建一个工单让技术支持人员检查下是什么情况。说不定对方是个“机器人”。我们甚至不必知道“正常的行为”是什么样，只需把用户的行为数据传给模型，让机器来决定对方是否是个“典型的”用户。这种方法虽然效果不如分类算法那样好，但仍值得一试。

降维(Dimensionality Reduction)

“将特定的特征组装成更高级的特征 ”

“降维”算法目前用于：

推荐系统

漂亮的可视化

主题建模和查找相似文档

假图识别

风险管理

常用的“降维”算法：

主成分分析(Principal Component Analysis ,PCA)

奇异值分解(Singular Value Decomposition ,SVD)

潜在狄里克雷特分配( Latent Dirichlet allocation, LDA)

潜在语义分析( Latent Semantic Analysis ,LSA, pLSA, GLSA),

t-SNE (用于可视化)

早年间，“硬核”的数据科学家会使用这些方法，他们决心在一大堆数字中发现“有趣的东西”。Excel图表不起作用时，他们迫使机器来做模式查找的工作。于是他们发明了降维或者特征学习的方法。

将2D数据投影到直线上(PCA)

对人们来说，相对于一大堆碎片化的特征，抽象化的概念更加方便。举个例子，我们把拥有三角形的耳朵、长长的鼻子以及大尾巴的狗组合出“牧羊犬”这个抽象的概念。相比于特定的牧羊犬，我们的确丢失了一些信息，但是新的抽象概念对于需要命名和解释的场景时更加有用。作为奖励，这类“抽象的”模型学习速度更快，训练时用到的特征数量也更少，同时还减少了过拟合。

这些算法在“主题建模”的任务中能大显身手。我们可以从特定的词组中抽象出他们的含义。潜在语义分析(LSA)就是搞这个事情的，LSA基于在某个主题上你能看到的特定单词的频次。比如说，科技文章中出现的科技相关的词汇肯定更多些，或者政治家的名字大多是在政治相关的新闻上出现，诸如此类。

我们可以直接从所有文章的全部单词中来创建聚类，但是这么做就会丢失所有重要的连接(比如，在不同的文章中battery 和 accumulator的含义是一样的)，LSA可以很好地处理这个问题，所以才会被叫做“潜在语义”(latent semantic)。

因此，需要把单词和文档连接组合成一个特征，从而保持其中的潜在联系——人们发现奇异值分解(SVD)能解决这个问题。那些有用的主题簇很容易从聚在一起的词组中看出来。

推荐系统和协同过滤是另一个高频使用降维算法的领域。如果你用它从用户的评分中提炼信息，你就会得到一个很棒的系统来推荐电影、音乐、游戏或者你想要的任何东西。

要完全理解这种机器上的抽象几乎不可能，但可以留心观察一些相关性：有些抽象概念和用户年龄相关——小孩子玩“我的世界”或者观看卡通节目更多，其他则可能和电影风格或者用户爱好有关。

仅仅基于用户评分这样的信息，机器就能找出这些高等级的概念，甚至不用去理解它们。干得漂亮，电脑先生。现在我们可以写一篇关于“为什么大胡子的伐木工喜欢我的小马驹”的论文了。

关联规则学习(Association rule learning)

“在订单流水中查找模式”

“关联规则”目前用于：

预测销售和折扣

分析“一起购买”的商品

规划商品陈列

分析网页浏览模式

常用的算法：

Apriori

Euclat

FP-growth

用来分析购物车、自动化营销策略以及其他事件相关任务的算法都在这儿了。如果你想从某个物品序列中发现一些模式，试试它们吧。

比如说，一位顾客拿着一提六瓶装的啤酒去收银台。我们应该在结账的路上摆放花生吗?人们同时购买啤酒和花生的频次如何？是的，关联规则很可能适用于啤酒和花生的情形，但是我们还可以用它来预测其他哪些序列? 能否做到在商品布局上的作出微小改变就能带来利润的大幅增长？

这个思路同样适用电子商务，那里的任务更加有趣——顾客下次要买什么？

不知道为啥规则学习在机器学习的范畴内似乎很少提及。经典方法是在对所有购买的商品进行正面检查的基础上套用树或者集合方法。算法只能搜索模式，但没法在新的例子上泛化或再现这些模式。

现实世界中，每个大型零售商都会建立了自己专属的解决方案，所以这里不会为你带来革命。

算法应用 

简而言之，任何定义明确的计算步骤都可称为算法，接受一个或一组值为输入，输出一个或一组值。

可以这样理解，算法是用来解决特定问题的一系列步骤（不仅计算机需要算法，我们在日常生活中也在使用算法）。算法必须具备如下 3 个重要特性：

• 有穷性，执行有限步骤后，算法必须中止。

• 确切性，算法的每个步骤都必须确切定义。

• 可行性，特定算法须可以在特定的时间内解决特定问题。

其实，算法虽然广泛应用在计算机领域，但却完全源自数学。实际上，最早的数学算法可追溯到公元前 1600 年 - Babylonians 有关求因式分解和平方根的算法。

01归并排序 (MERGE SORT)、快速排序 (QUICK SORT) 和堆积排序 (HEAP SORT)

 

 

哪个排序算法效率最高？这要看情况。这也就是我把 3 种算法放在一起讲的原因，可能你更常用其中一种，不过它们各有千秋。

归并排序算法，是目前为止最重要的算法之一，是分治法的一个典型应用，由数学家 John von Neumann 于 1945 年发明。

快速排序算法，结合了集合划分算法和分治算法，不是很稳定，但在处理随机列阵 (AM-based arrays) 时效率相当高。

堆积排序，采用优先伫列机制，减少排序时的搜索时间，同样不是很稳定。

与早期的排序算法相比 (如冒泡算法)，这些算法将排序算法提上了一个大台阶。也多亏了这些算法，才有今天的数据发掘，人工智能，链接分析，以及大部分网页计算工具。

02傅立叶变换和快速傅立叶变换

这两种算法简单，但却相当强大，整个数字世界都离不开它们，其功能是实现时间域函数与频率域函数之间的相互转化。能看到这篇文章，也是托这些算法的福。

因特网，WIFI，智能机，座机，电脑，路由器，卫星等几乎所有与计算机相关的设备都或多或少与它们有关。不会这两种算法，你根本不可能拿到电子，计算机或者通信工程学位。(USA)

03迪杰斯特拉算法 (Dijkstra’s algorithm)

 

可以这样说，如果没有这种算法，因特网肯定没有现在的高效率。只要能以 “图” 模型表示的问题，都能用这个算法找到 “图” 中两个节点间的最短距离。

虽然如今有很多更好的方法来解决最短路径问题，但代克思托演算法的稳定性仍无法取代。

04RSA 非对称加密算法

毫不夸张地说，如果没有这个算法对密钥学和网络安全的贡献，如今因特网的地位可能就不会如此之高。现在的网络毫无安全感，但遇到钱相关的问题时我们必需要保证有足够的安全感，如果你觉得网络不安全，肯定不会傻乎乎地在网页上输入自己的银行卡信息。

RSA 算法，密钥学领域最牛叉的算法之一，由 RSA 公司的三位创始人提出，奠定了当今的密钥研究领域。用这个算法解决的问题简单又复杂：保证安全的情况下，如何在独立平台和用户之间分享密钥。

05哈希安全算法 (Secure Hash Algorithm)

确切地说，这不是一种算法，而是一组加密哈希函数，由美国国家标准技术研究所首先提出。无论是你的应用商店，电子邮件和杀毒软件，还是浏览器等等，都使用这种算法来保证你正常下载，以及是否被 “中间人攻击”，或者 “网络钓鱼”。

06整数质因子分解算法 (Integer factorization)

这其实是一个数学算法，不过已经广泛应用与计算机领域。如果没有这个算法，加密信息也不会如此安全。通过一系列步骤将，它可以将一个合成数分解成不可再分的数因子。

很多加密协议都采用了这个算法，就比如刚提到的 RSA 算法。

07链接分析算法 (Link Analysis)

在因特网时代，不同入口间关系的分析至关重要。从搜索引擎和社交网站，到市场分析工具，都在不遗余力地寻找因特网的正真构造。

链接分析算法一直是这个领域最让人费解的算法之一，实现方式不一，而且其本身的特性让每个实现方式的算法发生异化，不过基本原理却很相似。

链接分析算法的机制其实很简单：你可以用矩阵表示一幅 “图 “，形成本征值问题。本征值问题可以帮助你分析这个 “图” 的结构，以及每个节点的权重。这个算法于 1976 年由 Gabriel Pinski 和 Francis Narin 提出。

谁会用这个算法呢？Google 的网页排名，Facebook 向你发送信息流时 (所以信息流不是算法，而是算法的结果)，Google + 和 Facebook 的好友推荐功能，LinkedIn 的工作推荐，Youtube 的视频推荐，等等。

普遍认为 Google 是首先使用这类算法的机构，不过其实早在 1996 年 (Google 问世 2 年前) 李彦宏就创建的 “RankDex” 小型搜索引擎就使用了这个思路。而 Hyper Search 搜索算法建立者马西莫・马奇奥里也曾使用过类似的算法。这两个人都后来都成为了 Google 历史上的传奇人物。

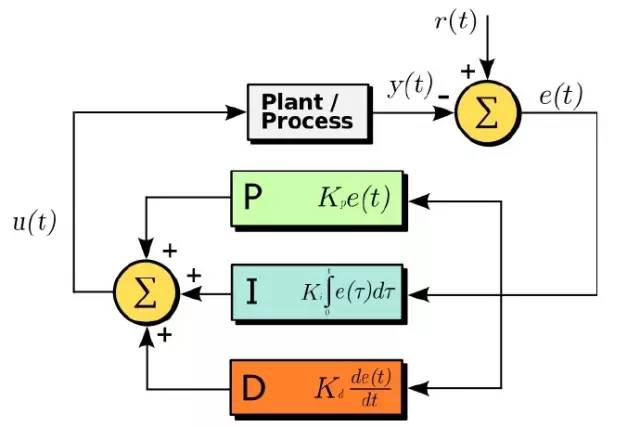
08比例微积分算法 (Proportional Integral Derivative Algorithm)

 

飞机，汽车，电视，手机，卫星，工厂和机器人等等事物中都有这个算法的身影。

简单来讲，这个算法主要是通过 “控制回路反馈机制”，减小预设输出信号与真实输出信号间的误差。只要需要信号处理，或电子系统来控制自动化机械，液压和加热系统，都需要用到这个算个法。

没有它，就没有现代文明。

09数据压缩算法

数据压缩算法有很多种，哪种最好？这要取决于应用方向，压缩 mp3，JPEG 和 MPEG-2 文件都不一样。

哪里能见到它们？不仅仅是文件夹中的压缩文件。你正在看的这个网页就是使用数据压缩算法将信息下载到你的电脑上。除文字外，游戏，视频，音乐，数据储存，云计算等等都是。它让各种系统更轻松，效率更高。

010随机数生成算法

到如今，计算机还没有办法生成 “真正的” 随机数，但伪随机数生成算法就足够了。这些算法在许多领域都有应用，如网络连接，加密技术，安全哈希算法，网络游戏，人工智能，以及问题分析中的条件初始化。