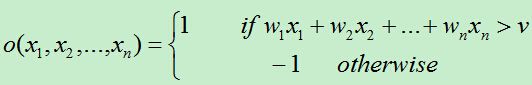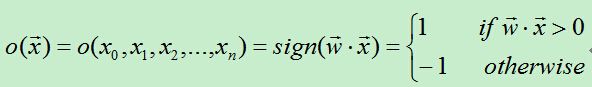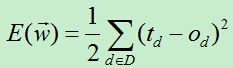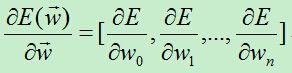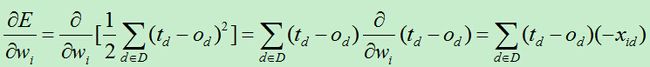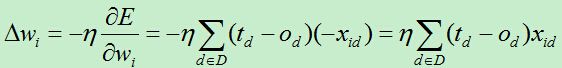感知器算法原理详解及python实现
感知器算法PLA
感知器算法是对一种分类学习机模型的称呼,属于有关机器学习的仿生学领域中的问题,由于无法实现非线性分类而下马。但“赏罚概念(reward-punishment concept)” 得到广泛应用。
感知器算法的原理:
感知器作为人工神经网络中最基本的单元,有多个输入和一个输出组成。虽然我们的目的是学习很多神经单元互连的网络,但是我们还是需要先对单个的神经单元进行研究。
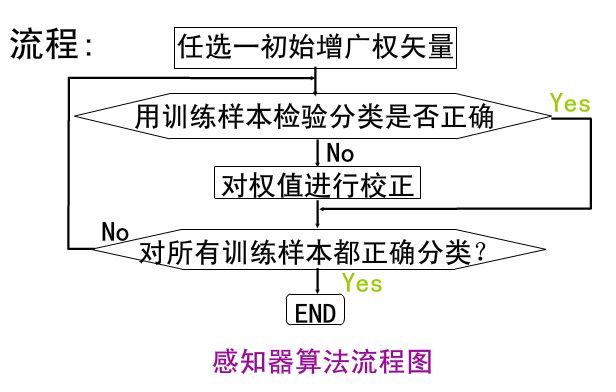
感知器算法的主要流程:
首先得到n个输入,再将每个输入值加权,然后判断感知器输入的加权和最否达到某一阀值v,若达到,则通过sign函数输出1,否则输出-1。
为了统一表达式,我们将上面的阀值v设为-w0,新增变量x0=1,这样就可以使用w0x0+w1x1+w2x2+…+wnxn>0来代替上面的w1x1+w2x2+…+wnxn>v。于是有:
从上面的公式可知,当权值向量确定时,就可以利用感知器来做分类。
那么我们如何获得感知器的权值呢?这需要根据训练集是否可分来采用不同的方法:
1、训练集线性可分时 --> 感知器训练法则
为了得到可接受的权值,通常从随机的权值开始,然后利用训练集反复训练权值,最后得到能够正确分类所有样例的权向量。
具体算法过程如下:
A)初始化权向量w=(w0,w1,…,wn),将权向量的每个值赋一个随机值。
B)对于每个训练样例,首先计算其预测输出:
C)当预测值不等于真实值时则利用如下公式修改权向量:
![]()
各符号含义: ![]() 代表学习速率,t代表样例的目标输出,o代表感知器输出。
代表学习速率,t代表样例的目标输出,o代表感知器输出。
D)重复B)和C),直到训练集中没有被错分的样例。
算法分析:
若某个样例被错分了,假如目标输出t为-1,结果感知器o输出为1,此时为了让感知器输出-1,需要将wx减小以输出-1,而在x的值不变的情况下只能减小w的值,这时通过在原来w后面添加(t-o)x=即可减小w的值(t-o<0, x>0)。
通过逐步调整w的值,最终感知器将会收敛到能够将所有训练集正确分类的程度,但前提条件是训练集线性可分。若训练集线性不可分,则上述过程不会收敛,将无限循环下去。
2、训练集线性不可分时 --> delta法则(又叫增量法则, LMS法则,Adaline法则,Windrow-Hoff法则)
由于在真实情况下,并不能保证训练集是线性可分的。因而,当训练集线性不可分时该如何训练感知器呢?这时我们使用delta法则,通过这种方式可以找出收敛到目标的最佳近似值,
delta法则的关键思想是使用梯度下降来搜索可能的权向量的假设空间,以找到最佳的拟合样例的权向量[1]。具体来说就是利用损失函数,每次向损失函数的负梯度方向移动,直到损失函数取得最小值(极小值)。我们将训练误差函数定义为:
其中D:训练集合,td为目标输出,od为感知器输出.
随机梯度下降算法过程如下:
1)初始化权向量w,将权向量的每个值取一个随机值。
2)对每个训练样例,分别执行以下操作:
A)通过感知器得到样例的输出o。
B)根据感知器的输出,修改权向量w。
3)重复第2)步,当训练样例的误差率小于设定的阀值时,算法终止。
算法条件:误差损失函数需要对权向量可微;假设空间包含连续参数化的假设。
可能存在的问题:若误差曲面有多个局部极小值,则不能保证达到全局最优。
算法第2)步的权向量公式的推导?请参考下一节梯度下降法则的推导。
二个区别:
1)感知器训练法则 和 delta法则(增量法则)
关键区别在于:感知器训练法则根据阀值化的感知器输出的误差更新权值;而增量法则根据输入的非阀值化线性组合的误差来更新权值。
二者的权值更新公式看似一样,实则不同:感知器法则的o是指阀值的输出:,而增量法则中的o是线性单元的输出:
2)(标准)梯度下降 和 随机梯度下降
梯度下降每轮遍历所有训练样例,将每个样例得到权向量的差值进行累加,最终将这些差值之和累加到初始的权向量上;而随机梯度下降则是在每个训练样例中都会更新权重,最终得到一个损失函数较小的权向量。
3、梯度下降法则的推导
梯度下降算法的核心就是每次向损失函数下降最陡峭的方向移动,而最陡峭的方向通常就是损失函数对权向量求偏导数得到的向量的反方向。
为了计算以上向量,我们逐个计算每个分量:
每次的权重更新量为:
使用这种方法来进行权重更新的方法叫做梯度下降,此方法将所有训练集权值计算了一个总和,然后将权值更新。此方法更新依次权值需要将所有训练集全部训练一次,故而速度较慢,效率较低。
为此改进这种蜗牛的更新速度,于是有了随机梯度下降算法,权向量更新公式为:
它在每个样例中迭代的过程中都会进行权值更新,通过这种方式能更加灵活的调整权值,使得权值以更快的速度收敛。
看着上面的那么复杂,下面简化的说一下步骤
感知器算法的实现步骤:
感知器算法的python代码实现:
# file name: Preception
# function: 感知器算法
# author:***
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def perception(W, w1, w2):
flag = False
while flag != True:
for i in range(len(w1)):
t1 = 0
t2 = 0
for j in range(len(W)):
t1 += W[j] * w1[i][j]
t2 += W[j] * w2[i][j]
if(t1 <= 0):
for j in range(len(W)):
W[j] += w1[i][j]
flag = False
break
if(t2 >= 0):
for j in range(len(W)):
W[j] -= w2[i][j]
flag = False
break
flag = True
print("判别函数:" + "d(x)= %d" % (W[0]) + "x" + "%d" % (W[1]) + "y" + "%d" % (W[2]) + "z+" + "%d" % (W[3]))
return W
if __name__ == '__main__':
W = [-1, -2, -2, 0]
w1 = [[0, 0, 0, 1], [1, 0, 0, 1], [1, 0, 1, 1], [1, 1, 0, 1]]
w2 = [[0, 0, 1, 1], [0, 1, 1, 1], [0, 1, 0, 1], [1, 1, 1, 1]]
W = perception(W, w1, w2)
fig = plt.figure()
ax = Axes3D(fig)
for i in range(len(w1)):
ax.scatter(w1[i][0],w1[i][1],w1[i][2],c = 'r',marker='*')
ax.scatter(w2[i][0],w2[i][1],w2[i][2],c = 'b',marker='o')
plt.grid()
xmin = min(min(w1[:][0]), min(w2[:][0]))
xmax = max(max(w1[:][0]), max(w2[:][0]))
ymin = min(min(w1[:][1]), min(w2[:][1]))
ymax = max(max(w1[:][1]), max(w2[:][1]))
x = np.linspace(xmin, xmax, 10)
y = np.linspace(ymin, ymax, 10)
x, y = np.meshgrid(x, y)
z = []
for i in range(len(x)):
z.append(((W[0]*x[i] + W[1]*y[i] + W[3]) / (-W[2])))
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()