CS224d Assignment Word2Vec

Word2Vec 练习题


$$y_o=P(o|c)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{V}exp(u_w^T{v}_c)}$$
$o$：输出词汇索引
$c$：中心词汇索引
$v_c$：中心词汇向量
$u_o$：输出词汇向量

设d为词向量维度，由图可知：
$$\theta =U^T{v}_c\in W\times 1$$
$$y_o=P(o|c)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{V}exp(u_w^T{v}_c)}=softmax(\theta {)}_o$$
按提示：


对所有的w对$u_w$求导数，即对U求导数。

由题损失函数为：



为更便于做题，先画一个简单的图进行CBOW模型和Skipgram模型的对比：

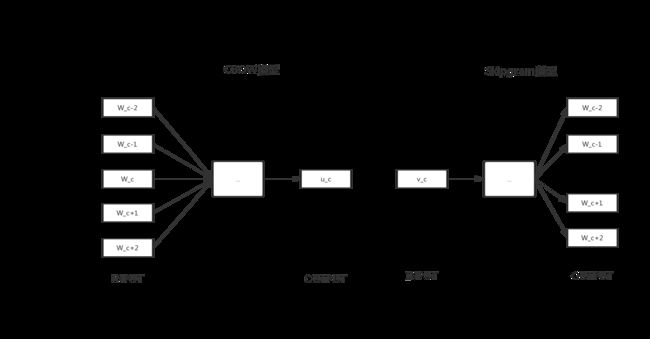
在skipgram模型中：

$$\frac{\partial J}{\partial v_c}=\sum _{-m\le j\le m,j̸=0}\frac{\partial F(w_{c+j},v_c)}{\partial v_c}$$
$$\frac{\partial J}{\partial v_j}为零向量，j̸=c$$
在CBOW模型中：
有上述对比图可知，CBOW模型由多个上下文词预测中心词，

$$\frac{\partial J}{\partial v_c}=\frac{\partial F(w_c,v)}{\partial v_c}为零向量$$
$$\frac{\partial J}{\partial v_j}=\frac{\partial F(w_c,v)}{\partial v}\cdot \frac{\partial v}{v_j}=\frac{\partial F(w_c,v)}{v_j}$$

import numpy as np
import random

from q1_softmax import softmax
from q2_gradcheck import gradcheck_naive
from q2_sigmoid import sigmoid, sigmoid_grad

def normalizeRows(x):
    """
        行归一化
    """

    N = x.shape[0]
    x /= np.sqrt(np.sum(x**2, axis=1)).reshape((N,1)) + 1e-30

    return x

def test_normalize_rows():
    print("Testing normalizeRows...")
    x = normalizeRows(np.array([[3.0,4.0],[1, 2]]))
    # result should be [[0.6, 0.8], [0.4472, 0.8944]]
    print(x)
    assert (np.amax(np.fabs(x - np.array([[0.6,0.8],[0.4472136,0.89442719]]))) <= 1e-6)


def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
    """
        word2vec的Softmax损失函数
    """

    # 输入:
    # - predicted: 预测词向量的numpy数组
    # - target: 目标词的下标
    # - outputVectors: 所有token的"output"向量(行形式)
    # - dataset: 用来做负例采样

    # 输出:
    # - cost: 输出的互熵损失
    # - gradPred: the gradient with respect to the predicted word
    #        vector
    # - grad: the gradient with respect to all the other word
    #        vectors

    probabilities = softmax(predicted.dot(outputVectors.T))
    cost = -np.log(probabilities[target])
    delta = probabilities
    delta[target] -= 1
    N = delta.shape[0]
    D = predicted.shape[0]
    grad = delta.reshape((N,1)) * predicted.reshape((1,D))
    gradPred = (delta.reshape((1,N)).dot(outputVectors)).flatten()

    return cost, gradPred, grad

def negSamplingCostAndGradient(predicted, target, outputVectors, dataset,
    K=10):
    """
        Word2vec模型负例采样后的损失函数和梯度
    """

    grad = np.zeros(outputVectors.shape)
    gradPred = np.zeros(predicted.shape)

    indices = [target]
    for k in xrange(K):
        newidx = dataset.sampleTokenIdx()
        while newidx == target:
            newidx = dataset.sampleTokenIdx()
        indices += [newidx]

    labels = np.array([1] + [-1 for k in xrange(K)])
    vecs = outputVectors[indices,:]

    t = sigmoid(vecs.dot(predicted) * labels)
    cost = -np.sum(np.log(t))

    delta = labels * (t - 1)
    gradPred = delta.reshape((1,K+1)).dot(vecs).flatten()
    gradtemp = delta.reshape((K+1,1)).dot(predicted.reshape(
        (1,predicted.shape[0])))
    for k in xrange(K+1):
        grad[indices[k]] += gradtemp[k,:]

     t = sigmoid(predicted.dot(outputVectors[target,:]))
     cost = -np.log(t)
     delta = t - 1

     gradPred += delta * outputVectors[target, :]
     grad[target, :] += delta * predicted

     for k in xrange(K):
         idx = dataset.sampleTokenIdx()

         t = sigmoid(-predicted.dot(outputVectors[idx,:]))
         cost += -np.log(t)
         delta = 1 - t

         gradPred += delta * outputVectors[idx, :]
         grad[idx, :] += delta * predicted
     return cost, gradPred, grad


def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
    dataset, word2vecCostAndGradient = softmaxCostAndGradient):
    """ Skip-gram model in word2vec """

    # skip-gram模型的实现

    # 输入:
    # - currrentWord: 当前中心词所对应的串
    # - C: 上下文大小(词窗大小)
    # - contextWords: 最多2*C个词
    # - tokens: 对应词向量中词下标的字典
    # - inputVectors: "input" word vectors (as rows) for all tokens
    # - outputVectors: "output" word vectors (as rows) for all tokens
    # - word2vecCostAndGradient: the cost and gradient function for a prediction vector given the target word vectors, could be one of the two cost functions you implemented above

    # 输出:
    # - cost: skip-gram模型算得的损失值
    # - grad: 词向量对应的梯度


    currentI = tokens[currentWord]
    predicted = inputVectors[currentI, :]

    cost = 0.0
    gradIn = np.zeros(inputVectors.shape)
    gradOut = np.zeros(outputVectors.shape)
    for cwd in contextWords:
        idx = tokens[cwd]
        cc, gp, gg = word2vecCostAndGradient(predicted, idx, outputVectors, dataset)
        cost += cc
        gradOut += gg
        gradIn[currentI, :] += gp

    return cost, gradIn, gradOut


def word2vec_sgd_wrapper(word2vecModel, tokens, wordVectors, dataset, C, word2vecCostAndGradient = softmaxCostAndGradient):
    batchsize = 50
    cost = 0.0
    grad = np.zeros(wordVectors.shape)
    N = wordVectors.shape[0]
    inputVectors = wordVectors[:N/2,:]
    outputVectors = wordVectors[N/2:,:]
    for i in xrange(batchsize):
        C1 = random.randint(1,C)
        centerword, context = dataset.getRandomContext(C1)

        if word2vecModel == skipgram:
            denom = 1
        else:
            denom = 1

        c, gin, gout = word2vecModel(centerword, C1, context, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient)
        cost += c / batchsize / denom
        grad[:N/2, :] += gin / batchsize / denom
        grad[N/2:, :] += gout / batchsize / denom

    return cost, grad

def test_word2vec():
    # Interface to the dataset for negative sampling
    dataset = type('dummy', (), {})()
    def dummySampleTokenIdx():
        return random.randint(0, 4)

    def getRandomContext(C):
        tokens = ["a", "b", "c", "d", "e"]
        return tokens[random.randint(0,4)], [tokens[random.randint(0,4)] \
           for i in xrange(2*C)]
    dataset.sampleTokenIdx = dummySampleTokenIdx
    dataset.getRandomContext = getRandomContext

    random.seed(31415)
    np.random.seed(9265)
    dummy_vectors = normalizeRows(np.random.randn(10,3))
    dummy_tokens = dict([("a",0), ("b",1), ("c",2),("d",3),("e",4)])
    print("==== Gradient check for skip-gram ====")
    gradcheck_naive(lambda vec: word2vec_sgd_wrapper(skipgram, dummy_tokens, vec, dataset, 5), dummy_vectors)
    gradcheck_naive(lambda vec: word2vec_sgd_wrapper(skipgram, dummy_tokens, vec, dataset, 5, negSamplingCostAndGradient), dummy_vectors)
    print("\n==== Gradient check for CBOW      ====")
    gradcheck_naive(lambda vec: word2vec_sgd_wrapper(cbow, dummy_tokens, vec, dataset, 5), dummy_vectors)
    gradcheck_naive(lambda vec: word2vec_sgd_wrapper(cbow, dummy_tokens, vec, dataset, 5, negSamplingCostAndGradient), dummy_vectors)

    print("\n=== Results ===")
    print(skipgram("c", 3, ["a", "b", "e", "d", "b", "c"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset))
    print(skipgram("c", 1, ["a", "b"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset, negSamplingCostAndGradient))
   # print(cbow("a", 2, ["a", "b", "c", "a"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset))
    #print(cbow("a", 2, ["a", "b", "a", "c"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset, negSamplingCostAndGradient))

if __name__ == "__main__":
    test_normalize_rows()
    test_word2vec()

import glob
import random
import numpy as np
import os.path as op
import _pickle as pickle

def load_saved_params():
    """ A helper function that loads previously saved parameters and resets iteration start """
    st = 0
    for f in glob.glob("saved_params_*.npy"):
        iter = int(op.splitext(op.basename(f))[0].split("_")[2])
        if (iter > st):
            st = iter
            
    if st > 0:
        with open("saved_params_%d.npy" % st, "r") as f:
            params = pickle.load(f)
            state = pickle.load(f)
        return st, params, state
    else:
        return st, None, None
    
def save_params(iter, params):
    with open("saved_params_%d.npy" % iter, "w") as f:
        pickle.dump(params, f)
        pickle.dump(random.getstate(), f)

def sgd(f, x0, step, iterations, postprocessing = None, useSaved = False, PRINT_EVERY=10):
    """ Stochastic Gradient Descent """
    # Implement the stochastic gradient descent method in this        
    # function.                                                       
    
    # Inputs:                                                         
    # - f: the function to optimize, it should take a single        
    #     argument and yield two outputs, a cost and the gradient  
    #     with respect to the arguments                            
    # - x0: the initial point to start SGD from                     
    # - step: the step size for SGD                                 
    # - iterations: total iterations to run SGD for                 
    # - postprocessing: postprocessing function for the parameters  
    #     if necessary. In the case of word2vec we will need to    
    #     normalize the word vectors to have unit length.          
    # - PRINT_EVERY: specifies every how many iterations to output  

    # Output:                                                         
    # - x: the parameter value after SGD finishes  
    
    # Anneal learning rate every several iterations
    ANNEAL_EVERY = 20000
    
    if useSaved:
        start_iter, oldx, state = load_saved_params()
        if start_iter > 0:
            x0 = oldx;
            step *= 0.5 ** (start_iter / ANNEAL_EVERY)
            
        if state:
            random.setstate(state)
    else:
        start_iter = 0
    
    x = x0
    
    if not postprocessing:
        postprocessing = lambda x: x
    
    expcost = None
    
    for iter in range(start_iter + 1, iterations + 1):
        ### Don't forget to apply the postprocessing after every iteration!
        ### You might want to print the progress every few iterations.

        cost = None
        ### YOUR CODE HERE
        cost, f_grad = f(x)
        # 根据梯度来更新x，也就是下降x
        x -= step * f_grad
        x = postprocessing(x)

        ### END YOUR CODE
        
        if iter % PRINT_EVERY == 0:
            if not expcost:
                expcost = cost
            else:
                expcost = .95 * expcost + .05 * cost
            print("iter %d: %f" % (iter, expcost))
        
        if iter % SAVE_PARAMS_EVERY == 0 and useSaved:
            save_params(iter, x)
            
        if iter % ANNEAL_EVERY == 0:
            step *= 0.5
    
    return x

def sanity_check():
    quad = lambda x: (np.sum(x ** 2), x * 2)

    print("Running sanity checks...")
    t1 = sgd(quad, 0.5, 0.01, 1000, PRINT_EVERY=100)
    print("test 1 result:", t1)
    assert abs(t1) <= 1e-6

    t2 = sgd(quad, 0.0, 0.01, 1000, PRINT_EVERY=100)
    print("test 2 result:", t2)
    assert abs(t2) <= 1e-6

    t3 = sgd(quad, -1.5, 0.01, 1000, PRINT_EVERY=100)
    print("test 3 result:", t3)
    assert abs(t3) <= 1e-6
    
    #print ""


if __name__ == "__main__":
    sanity_check();
   # your_sanity_checks();