平面点云凸包曲线计算

平面点云凸包曲线计算

---

解法一

主要思想：分而治之
算法流程：

1. 如图，先找出y坐标最大和做小的点，并入此多边形的顶点集（因为是y坐标最大和最小，所以此直线左边和右边的凸包合起来还是凸包)；
   
2. 对直线左右的点进行递归处理
   2.1如直线左边，先找到一个离直线最远的点p并入多边形顶点集，连接p和ymin和ymax(因为是离直线d最远的点， 所以直线a左边的凸包和b上边的凸包合起来还是凸包，如图：
   
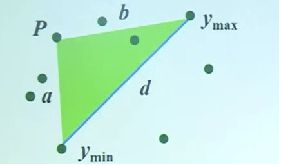
   2.2将三角形内部的点删除，这部分点必然不是凸包上的点（这一步可以写也可以不写，如果不写，在后续判断中也不会将这些点判断为凸包上的点，只是会增大计算量）
   2.3分别对直线a左边和直线b上边的点递归处理

算法时间复杂度：O(n^2)

测试代码

说明：

1. 编程语言为C++
2. 以链表的形式存储点（希望得到的轮廓点按照一定的顺序排列），
   链表的形式方便元素的插入和删除，但是不利于元素的随机访问，后改为使用容器存储
3. 使用第三方库（opencv），版本为2.4.8

struct PointCloud_Xu
{
	Point2f point;
	bool flag = false;  //用于记录该点是否已经经过判定（无论是凸包上的点还是其他点）
	void clear()
	{
		point = Point2f(0.0f, 0.0f);
		flag = false;
	}
};

double D_Point_Line2(Point2f P_start, Point2f P_end, Point2f P)
{
	double result;
	double t1 = (P_start.x - P.x) * (P_start.x - P_end.x);
	double t2 = (P_start.y - P.y) * (P_start.y - P_end.y);
	double t3 = 0;
	double t4 = pow((P_start.x - P_end.x), 2.0) + pow((P_start.y - P_end.y), 2.0);
	double t = (t1 + t2 + t3) / t4;
	//求垂足（XYZ）
	double X = P_start.x + t * (P_end.x - P_start.x);
	double Y = P_start.y + t * (P_end.y - P_start.y);
	double Z = 0;
	result = sqrt(pow((X - P.x), 2.0) + pow((Y - P.y), 2.0));
	return result;
}

void Max_Distance_Point(vector& P, Point2f P_start, Point2f P_end, Point2f center)
{
	//Contour只包含两个点（初始状态）
	if (center.x == (P_start.x + P_end.x) / 2.0 &&
		center.y == (P_start.y + P_end.y) / 2.0)
	{
		int N1 = -1;
		double D1 = -10;
		int N2 = -1;
		double D2 = -10;
		for (size_t i = 0; i < P.size(); i++)
		{
			if (P.at(i).flag == false)
			{
				Point2f V1 = P_end - P_start;
				Point2f V2 = P.at(i).point - P_start;
				if (V1.x*V2.y - V2.x*V1.y > 0)
				{
					double d1 = D_Point_Line2(P_start, P_end, P.at(i).point);
					if (d1>D1)
					{
						D1 = d1;
						N1 = i;
					}
				}
				else
				{
					double d2 = D_Point_Line2(P_start, P_end, P.at(i).point);
					if (d2 > D2)
					{
						D2 = d2;
						N2 = i;
					}
				}
			}
		}
		P.at(N1).flag = true;
		P.at(N2).flag = true;
	}
	//非初始状态
	else
	{
		int N1 = -1;
		double D1 = -10;
		for (size_t i = 0; i D1)
					{
						D1 = d1;
						N1 = i;
					}
				}
			}
		}
		if (N1 != -1)
		{
			P.at(N1).flag = true;
		}
	}
}

main()
{
	//计算包络线			
	vector P;
	if (!P.empty())
	{
		P.clear();
	}
	string path_section = path_section1 + to_string(_ULONGLONG(i)) + ".txt";
	inFlie.open(path_section);
	if (!inFlie.is_open())
	{
		return;
	}
	for (size_t j = 0; j < 200; j++)
	{
		PointCloud_Xu P_tmp;
		inFlie >> P_tmp.point.x;
		inFlie >> P_tmp.point.y;
		P_tmp.flag = false;
		P.push_back(P_tmp);
	}
	inFlie.close();
	//确定Ymax,Ymin
	double Ymax = -10000;
	double Ymin = 10000;
	int Nmax = -1; //Ymax的序列号
	int Nmin = -1; //Ymin的序列号
	for (size_t j = 0; j < P.size(); j++)
	{
		if (P.at(j).point.y > Ymax)
		{
			Ymax = P.at(j).point.y;
			Nmax = j;
		}
		if (P.at(j).point.y < Ymin)
		{
			Ymin = P.at(j).point.y;
			Nmin = j;
		}
	}
	P.at(Nmax).flag = true;
	P.at(Nmin).flag = true;

	vector contour;
	if (!contour.empty())
	{
		contour.clear();
	}
	if (Nmax > Nmin)
	{
		contour.push_back(P.at(Nmin).point);
		contour.push_back(P.at(Nmax).point);
	}
	else
	{
		contour.push_back(P.at(Nmax).point);
		contour.push_back(P.at(Nmin).point);
	}

	Point2f center = P.at(Nmax).point + P.at(Nmin).point;
	center.x /= 2.0;
	center.y /= 2.0;

	while (true)
	{
		int Contour_size = contour.size();
		for (size_t j = 0; j < Contour_size; j++)
		{
			if (Contour_size==2)
			{
				Max_Distance_Point(P, contour[0], contour[1], center);
				break;
			}
			else
			{
				Max_Distance_Point(P, contour[j], contour[(j+1)%contour.size()], center);
			}
		}
		contour.clear();
		for (size_t j = 0; j < P.size(); j++)
		{
			if (P.at(j).flag == true)
			{
				contour.push_back(P.at(j).point);
			}
		}
		if (Contour_size == contour.size())
		{
			break;
		}
	}
	//输出contour
	string path_out = path_out1 + to_string(_ULONGLONG(i)) + ".txt";
	outFile.open(path_out);
	for (size_t j = 0; j < contour.size(); j++)
	{
		outFile << contour[j].x << "  " << contour[j].y << endl;
	}
	outFile.close();

	Mat test = Mat(480, 640, CV_8UC3, Scalar::all(255));
	Point2f P_center = Point2f(0, 0);
	for (size_t j = 0; j < P.size(); j++)
	{
		P_center += P.at(j).point;
	}
	P_center.x /= P.size();
	P_center.y /= P.size();

	for (size_t j = 0; j < P.size(); j++)
	{
		circle(test, P[j].point - P_center + Point2f(320, 240), 0.5, Scalar(0, 0, 255), -1, 8, 0);
		line(test, P[j].point - P_center + Point2f(320, 240), P[(j + 1) % P.size()].point - P_center + Point2f(320, 240),
			Scalar(0, 0, 255), 1, 8, 0);
	}
	for (size_t j = 0; j < contour.size(); j++)
	{
		circle(test, contour[j] - P_center + Point2f(320, 240), 0.5, Scalar(255, 0, 0), -1, 8, 0);
		line(test, contour[j] - P_center + Point2f(320, 240), contour[(j + 1) % contour.size()] - P_center + Point2f(320, 240),
			Scalar(255, 0, 0), 1, 8, 0);
	}
	imshow("test", test);
	imwrite(path_out1 + to_string(_ULONGLONG(i)) + ".bmp", test);
	waitKey(0);
}

---

解法二

主要思想：类似于贪心算法
算法流程：

1. 确定点Xmax或者Xmin或Ymax或者Ymin，记为初始点
2. 遍历所有点，根据点和当前点构成的向量的方向，计算得到下一个轮廓点
3. 重复步骤2，直至最新得到的点为初始点

算法时间复杂度：O(n^2)
算法分析：需要事先知道所有点的坐标，一旦添加或者删除任意一个点，需要重新进行计算

解法三

主要思想：由局部到整体
算法流程：

1. 确定两个初始点Ymax以及Ymin（Xmax以及Xmin也可以）
2. 添加除了两个初始点之外的任意一个点
3. 添加剩余的任意一个点，判断该点在当前凸包内部还是外部，若在凸包内部，则判断下一个点，若在凸包外部，则修正凸包

算法分析：不需要事先知道所有点，可以在运算过程中随时增加点，但是也不能做到随时删除点