用C#实现计算机图形学算法
多数情况下计算机图形学算法都用C++实现,下面鄙人用C#实现一部分算法。并附上运行截图。
一 图案
1 金刚石
金刚石图案是每一个顶点都与其他顶点相连的正n边形。金刚石图案有时被用作计算机图形设备的测试图案。通过观察交汇于每个顶点的直线所呈现出来的拥挤和模糊程度,可以确定设备的分辨率。
做程序时,使用线段连接每个顶点时不进行重复连接。
主要代码如下:
//n为等分点的个数,r为圆的半径
Pen p = new Pen(Color.Blue, 1);//定义了一个蓝色,宽度为的画笔
double Thta;//thta为圆的等分角
Thta = 2 * PI / jgsn;
for (int i = 0; i < jgsn; i++)
{
pt[i].X = (int)(r * Math.Cos(i * Thta) + maxX / 2);
pt[i].Y = (int)(r * Math.Sin(i * Thta) + maxY / 2);
}
for (int i = 0; i <= jgsn - 2; i++)
{
for (int j = i + 1; j <= jgsn - 1; j++)
{
//dc.MoveTo(ROUND(pt3[i].x),ROUND(pt3[i].y));
//g.DrawLine(p,pt[i],pt[j]);
g.DrawLine(p, pt[i].X, pt[i].Y, pt[j].X, pt[j].Y);
//dc.LineTo(ROUND(pt3[j].x),ROUND(pt3[j].y));
}
}
运行结果如下:
金刚石图案按孔令德老师所说,等分点数为奇数时图案中心为一个圆,等分点数为偶数时图案中心为一个点,运行结果确实如此。
2 Menger海绵
将一个立方体沿其各个面三等分为27个小立方体,舍弃位于体心的一个小立方体,以及位于立方体六个面心处的6个小立方体。将剩余的20个小立方体继续按相同的方法分割与舍弃,就能得到中间有大量空隙的Menger海绵。
算法步骤:
输入递归深度n;
绘制初始立方体;
将立方体的每条边三等分,舍弃6个位于面心的小立方体和一个位于体心处的小立方体,使用画家算法绘制余下的20个小立方体;
执行递归子程序,对其余20个小立方体进行递归,直到n为0。
具体代码就不贴出了,有兴趣可以自己下载了查看;运行效果如下;
绘图时可以用C#的Point类型的数组表示点集,如果用C++的话通常需要自己定义一个二维点类。在编写图形学算法代码时,还会用到三维点类,这就需要自己定义了。
另外C#的二维数组定义与C++颇有不同,其定义类似如下;
private int[,] TM=new int[4,4];//变换矩阵
二维数组作函数参数的写法则类似如下,与C++不同;
private void KeepOriginalMatrix(int[,] Orig,int[,] Dest)
二 基本图元算法
1 圆中点Bresenham算法
Bresenham算法是计算机图形学领域使用广泛的直线扫描转换方法。其原理是:过各行、各列像素中心构造一组虚拟网格线,按直线从起点到终点的顺序计算直线各垂直网格线的交点,然后确定该列像素中与此交点最近的像素。
此处为了清楚演示计算机图形学的原理,并不画计算出的每一个点,而是先生成Button的控件数组,在每个点处放一个小Button,Button的长和宽为10;这样出来的效果相当于把屏幕单个像素放大了10倍;如下图所示;
设置Button数组坐标的代码如下,其他部分可自行下载查看;
private void CirclePoint(int x, int y,int cnt)//八分法画圆子函数
{
btny[0 + 8 * cnt].Left = x + maxX / 2 - 8;
btny[0 + 8 * cnt].Top = y + maxY / 2 - 8;
btny[1 + 8 * cnt].Left = y + maxX / 2 - 8;
btny[1 + 8 * cnt].Top = x + maxY / 2 - 8;
btny[2 + 8 * cnt].Left = y + maxX / 2 - 8;
btny[2 + 8 * cnt].Top = -x + maxY / 2 - 8;
btny[3 + 8 * cnt].Left = x + maxX / 2 - 8;
btny[3 + 8 * cnt].Top = -y + maxY / 2 - 8;
btny[4 + 8 * cnt].Left = -x + maxX / 2 - 8;
btny[4 + 8 * cnt].Top = -y + maxY / 2 - 8;
btny[5 + 8 * cnt].Left = -y + maxX / 2 - 8;
btny[5 + 8 * cnt].Top = -x + maxY / 2 - 8;
btny[6 + 8 * cnt].Left = -y + maxX / 2 - 8;
btny[6 + 8 * cnt].Top = x + maxY / 2 - 8;
btny[7 + 8 * cnt].Left = -x + maxX / 2 - 8;
btny[7 + 8 * cnt].Top = y + maxY / 2 - 8;
}
三 二维变换
1 首先绘制坐标系和基本图形
2 二维变换是通过矩阵运算完成的
相关代码如下;
private void DrawShape(Graphics g) //画四边形
{
KeepOriginalMatrix(P24, OSquare);
Pen pen = new Pen(Color.Green, 2);
g.DrawLine(pen, maxX / 2 + P24[0, 0], maxY / 2 - P24[0, 1], maxX / 2 + P24[1, 0], maxY / 2 - P24[1, 1]);
g.DrawLine(pen, maxX / 2 + P24[1, 0], maxY / 2 - P24[1, 1], maxX / 2 + P24[2, 0], maxY / 2 - P24[2, 1]);
g.DrawLine(pen, maxX / 2 + P24[2, 0], maxY / 2 - P24[2, 1], maxX / 2 + P24[3, 0], maxY / 2 - P24[3, 1]);
g.DrawLine(pen, maxX / 2 + P24[3, 0], maxY / 2 - P24[3, 1], maxX / 2 + P24[0, 0], maxY / 2 - P24[0, 1]);
}
private void KeepOriginalMatrix(int[,] Orig,int[,] Dest)//保留矩阵
{
int i,j;
for(i=0;i<4;i++)
for(j=0;j<3;j++)
Dest[i,j]=Orig[i,j];
}
private void Tmove(int Tx,int Ty)//平移变换矩阵
{
ClearMatrix(TM);
TM[0,0]=1;
TM[1,1]=1;
TM[2,0]=Tx;
TM[2,1]=Ty;
TM[2,2]=1;
Calculate(P24,TM);
}
private void Trotate(double thta)//旋转变换矩阵
{
ClearMatrix(TR2);
TR2[0,0]=(int) Math.Cos(thta*PI/180);
TR2[0, 1] = (int)Math.Sin(thta * PI / 180);
TR2[1, 0] = (int) -Math.Sin(thta * PI / 180);
TR2[1, 1] = (int)Math.Cos(thta * PI / 180);
TR2[2,2]=1;
Calculate(P24,TR2);
}
private void Tscale(double Sx,double Sy)//比例变换矩阵
{
ClearMatrix(TS2);
TS2[0,0]=(int)Sx;
TS2[1,1]=(int)Sy;
TS2[2,2]=1;
Calculate(P24,TS2);
}
private void Treform(double b,double c)//错切变换矩阵
{
ClearMatrix(TC2);
TC2[0,0]=1;
TC2[0,1]=(int)b;
TC2[1,0]=(int)c;
TC2[1,1]=1;
TC2[2,2]=1;
Calculate(P24,TC2);
}
private void ClearMatrix(int[,] A)//清除变换矩阵
{
for(int i=0;i<3;i++)
{
for(int j=0;j<3;j++)
A[i,j]=0;
}
}
private void Calculate(int[,] P0,int[,] T)//两个矩阵相乘
{
int[,] Ptemp=new int[4,3];
KeepOriginalMatrix(P24,Ptemp);
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 3; j++)
{
P24[i, j] = Ptemp[i, 0] * T[0, j] + Ptemp[i, 1] * T[1, j] + Ptemp[i, 2] * T[2, j];
}
}
}
下面是平移,缩放,错切的运行结果;从菜单中画初始图形;用四个方向键实现平移;用M键实现放大;用C和D键实现2个方向的错切;
四 基本三维
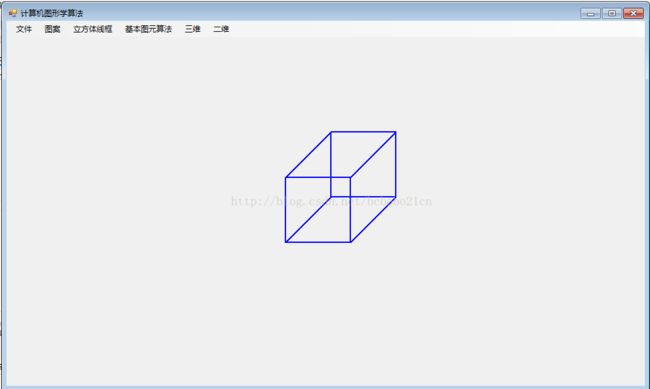
1 画一个三维立方体
主要代码如下;
private void DrawCube(Graphics g)//绘制立方体
{
Point[] p=new Point[4];//定义多边形顶点数组
Transform3DTo2D(P3D,P2D,8);
//绘制立方体左面
p[0]=new Point(maxX/2+P2D[0,0],(maxY/2+P2D[0,1]));
p[1]=new Point(maxX/2+P2D[3,0],(maxY/2+P2D[3,1]));
p[2]=new Point(maxX/2+P2D[7,0],(maxY/2+P2D[7,1]));
p[3]=new Point(maxX/2+P2D[4,0],(maxY/2+P2D[4,1]));
Pen pen = new Pen(Color.Blue, 2);
g.DrawLines(pen, p);
//绘制立方体后面
p[0]=new Point(maxX/2+P2D[0,0],(maxY/2+P2D[0,1]));
p[1]=new Point(maxX/2+P2D[1,0],(maxY/2+P2D[1,1]));
p[2]=new Point(maxX/2+P2D[2,0],(maxY/2+P2D[2,1]));
p[3]=new Point(maxX/2+P2D[3,0],(maxY/2+P2D[3,1]));
g.DrawLines(pen, p);
//绘制立方体底面
p[0]=new Point(maxX/2+P2D[0,0],(maxY/2+P2D[0,1]));
p[1]=new Point(maxX/2+P2D[4,0],(maxY/2+P2D[4,1]));
p[2]=new Point(maxX/2+P2D[5,0],(maxY/2+P2D[5,1]));
p[3]=new Point(maxX/2+P2D[1,0],(maxY/2+P2D[1,1]));
g.DrawLines(pen, p);
//绘制立方体右面
p[0]=new Point(maxX/2+P2D[1,0],(maxY/2+P2D[1,1]));
p[1]=new Point(maxX/2+P2D[2,0],(maxY/2+P2D[2,1]));
p[2]=new Point(maxX/2+P2D[6,0],(maxY/2+P2D[6,1]));
p[3]=new Point(maxX/2+P2D[5,0],(maxY/2+P2D[5,1]));
g.DrawLines(pen, p);
//绘制立方体顶面
p[0]=new Point(maxX/2+P2D[3,0],(maxY/2+P2D[3,1]));
p[1]=new Point(maxX/2+P2D[7,0],(maxY/2+P2D[7,1]));
p[2]=new Point(maxX/2+P2D[6,0],(maxY/2+P2D[6,1]));
p[3]=new Point(maxX/2+P2D[2,0],(maxY/2+P2D[2,1]));
g.DrawLines(pen, p);
//绘制立方体前面
p[0]=new Point(maxX/2+P2D[4,0],(maxY/2+P2D[4,1]));
p[1]=new Point(maxX/2+P2D[5,0],(maxY/2+P2D[5,1]));
p[2]=new Point(maxX/2+P2D[6,0],(maxY/2+P2D[6,1]));
p[3]=new Point(maxX/2+P2D[7,0],(maxY/2+P2D[7,1]));
g.DrawLines(pen, p);
}
效果如下;
代码和可执行文件下载:
http://pan.baidu.com/s/1hqF0Jic