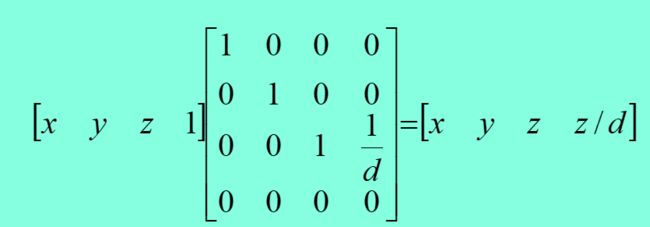计算机图形学算法总结
图形学算法总结
文章目录
- 图形学算法总结
-
- 直线生成算法
-
- 数值微分法(DDA)
- 中点画线法
- Bresenham算法
- 圆弧生成算法
-
- 中点Bresenham画圆法
- 多边形填充算法
-
- 逐点判断法
-
- 1)射线法
- 2)累计角度法
- 扫描线算法(YX)
- 改进的扫描线算法(Y-X)
- 边缘填充算法
- 区域种子填充算法
-
- 1)深度递归的种子填充算法(漫水法)
- 2)扫描线种子填充算法
- 反走样
-
- 简单区域采样(非加权区域采样)
- 加权区域采样
- 直线和多边形裁剪
-
- 编码裁剪
- 中点分割裁剪
- 梁友栋-Barskey算法
- 多边形逐边裁剪算法
- 双边裁剪算法
- 消隐
-
- 深度缓存算法(Z_Buffer算法)
- 扫描线算法
- 多边形区域排序算法
- 曲线曲面
-
- Hermite曲线
- Bezier曲线
- B样条曲线
- 图形变换
-
- 平移变换
- 比例变换
- 旋转变换
- 对称变换
- 错切变换
- 投影变换
-
- 正交平行投影
- 斜交投影
- 透视投影
直线生成算法
数值微分法(DDA)
y = k x + b y = kx + b y=kx+b
x每增加1,y增量为k
|k|要小于1,大于则互换x,y
原因:防止画出来的线太稀疏

| 象限 | |dx|>|dy|? | D x | D y |
|---|---|---|---|
| 1a | 是 | 1 | k |
| 1b | 否 | 1/k | 1 |
| 2a | 是 | -1 | k |
| 2b | 否 | -1/k | 1 |
| 3a | 是 | -1 | -k |
| 3b | 否 | -1/k | -1 |
| 4a | 是 | 1 | -k |
| 4b | 否 | 1/k | -1 |
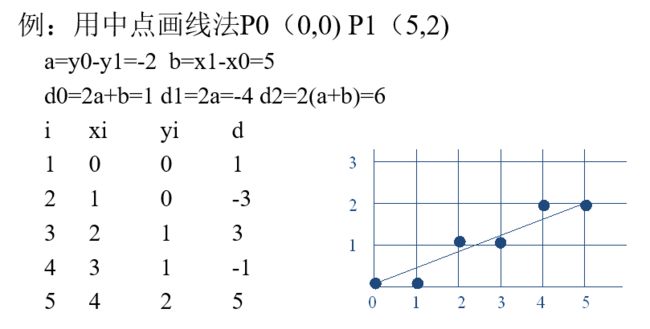
中点画线法
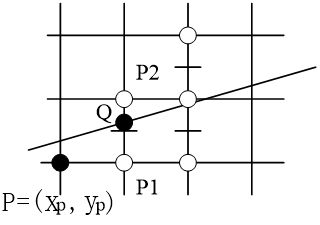
y = a x + b y + c y = ax + by +c y=ax+by+c
其中, a = y 0 − y 1 , b = x 1 − x 0 a=y_0-y_1,b=x_1-x_0 a=y0−y1,b=x1−x0
我们每次都把中点(x+1,y+0.5)带入方程,记结果为d,与0比较
-
d≥0 中点在直线上方,取 ( x i + 1 , y i ) (x_i+1,y_i) (xi+1,yi)
- d i + 1 = d i + a d_{i+1}=d_i+a di+1=di+a
-
d<0 中点在直线下方,取 ( x i + 1 , y i + 1 ) (x_i+1,y_i+1) (xi+1,yi+1)
- d i + 1 = d i + a + b d_{i+1}=d_i+a+b di+1=di+a+b
其中,初始值 d 0 = a + 0.5 b d_0 = a+0.5b d0=a+0.5b
可以用 2d 代替 d 来摆脱小数,提高效率。
Bresenham算法
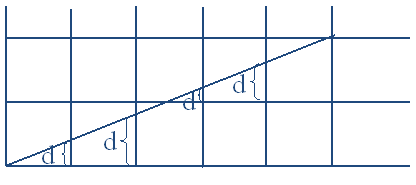
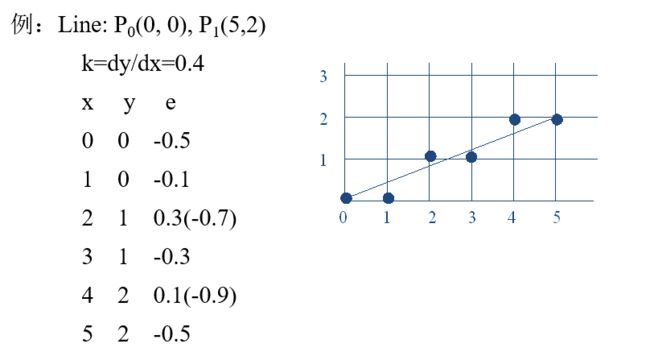
我们计算直线的斜率 k = d y d x k=\frac{dy}{dx} k=dxdy
和DDA一样,x每增加1,y增加k
于是,我们可以这样算:
d 0 = 0 d_0=0 d0=0 d i + 1 = d i + k d_{i+1} = d_i+k di+1=di+k
- d≥0.5 取 ( x i + 1 , y i + 1 ) (x_i+1,y_i+1) (xi+1,yi+1)
- d<0.5 取 ( x i + 1 , y i ) (x_i+1,y_i) (xi+1,yi)
当 d≥1 的时候 d = d − 1 d = d-1 d=d−1
当然,为了便于计算,可令 e = d − 0.5 e = d-0.5 e=d−0.5
e 0 = − 0.5 e_0=-0.5 e0=−0.5 e i + 1 = e i + k e_{i+1} = e_i+k ei+1=ei+k
- e≥0 取 ( x i + 1 , y i + 1 ) (x_i+1,y_i+1) (xi+1,yi+1)
- e<0 取 ( x i + 1 , y i ) (x_i+1,y_i) (xi+1,yi)
当 e≥0 的时候 e = e − 1 e = e-1 e=e−1
圆弧生成算法
中点Bresenham画圆法

d = x 2 + y 2 − R 2 d = x^2+y^2-R^2 d=x2+y2−R2
与前面类似 d 0 = 1.25 − R d_0=1.25-R d0=1.25−R
- d≥0 取 ( x i + 1 , y i − 1 ) (x_i+1,y_i-1) (xi+1,yi−1)
- d i + 1 = d i + 2 ( x p − y p ) + 5 d_{i+1}=d_i+2(x_p-y_p)+5 di+1=di+2(xp−yp)+5
- d<0 取 ( x i + 1 , y i ) (x_i+1,y_i) (xi+1,yi)
- d i + 1 = d i + + 2 x p + 3 d_{i+1}=d_i++2x_p+3 di+1=di++2xp+3
为方便计算,使用e=d-0.25代替d
多边形填充算法
逐点判断法
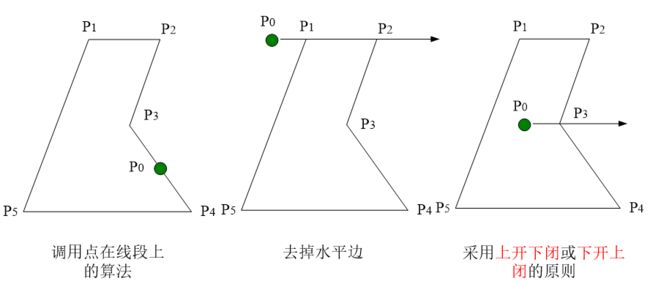
1)射线法
作射线求交点各数k
- k为奇数 点在多边形内
- k为偶数 点在多边形外
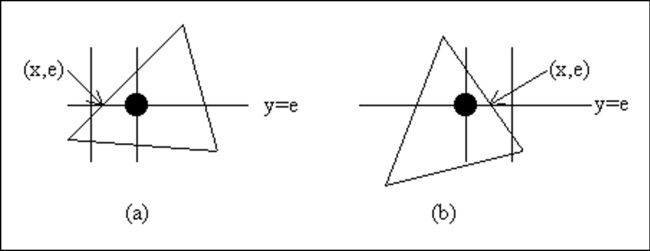
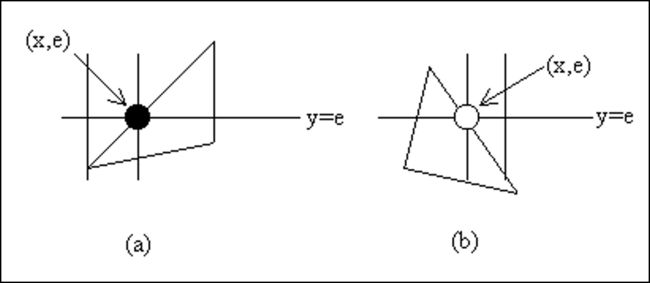
特殊情况:
2)累计角度法
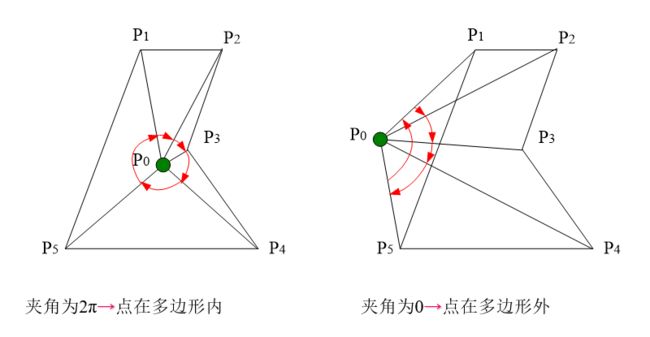
与各顶点连线,形成有向角 θ i \theta_i θi,然后作累加
- 结果为0 点在多边形外
- 结果为±2 π \pi π 点在多边形内
扫描线算法(YX)

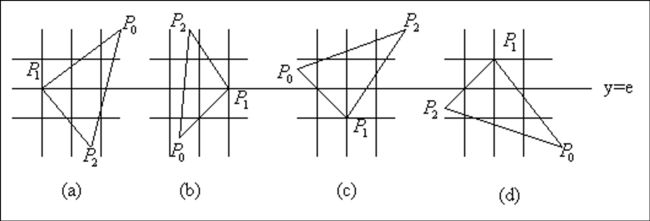
举个例子,6号扫描线与多边形交点并按x值递增排序为A,B,C,D
然后我们就开始配对,AB一对,CD一堆,并给AB和CD这两个线段填色。
依此类推,就能给多边形填完色。
改进的扫描线算法(Y-X)

活性边表: x x x △ x △x △x y m a x y_{max} ymax

边表桶:
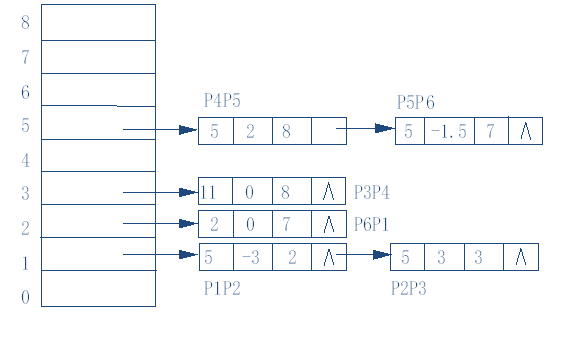
特殊情况:
边缘填充算法
对多边形上每一条非水平边上的每个象素开始向右求余

改进后有栅栏填充算法和边界标志算法
区域种子填充算法

1)深度递归的种子填充算法(漫水法)
-
种子入栈
-
栈非空,转3;栈空,结束
-
栈顶元素出栈,如果它未填充则填充,然后找其他方向未填充的点,将其入栈,找完所有方向后(4联通就是4个方向,8联通就是8个方向),转2
假设方向是上下左右,那么顺序就是
- 栈:H
- 填色:H 栈: I F J
- 填色:J 栈:I F K N
- 填色:N 栈:I F K M
- 填色:M 栈:I F K L
- 填色:L 栈:I F K
- 填色:K 栈:I F
- 填色:F 栈:I D G
- 填色:G 栈:I D E
- 填色:E 栈:I D
- 填色:D 栈:I C
- 填色:C 栈:I B
- 填色:B 栈:I A
- 填色:A 栈:I
- 填色:I
2)扫描线种子填充算法
其实就是种子填充的改进版,减少了递归次数
扫描线种子填充算法
-
初始化:堆栈置空。将种子点(x,y)入栈。
-
出栈:若栈空则结束。否则取栈顶元素(x,y),以y作为当前扫描线。
-
填充并确定种子点所在区段:从种子点(x,y)出发,沿当前扫描线向左、右两个方向填充,直到非内部。分别标记区段的左、右端点坐标为xl和xr。
-
并确定新的种子点:在区间[xl,xr]中检查与当前扫描线y上、下相邻的两条扫描线上的象素。若存在非边界、未填充的象素,则把每一区间的最右象素作为种子点压入堆栈,返回第(2)步。
- 填充DFHJM
- 上下搜寻
- DFHJM任意一个往下走填充EDIK
- N往上走填充M
- D往上走填充C
- 上下搜寻
- M往上走填充L
- C往上走填充B
- 上下搜寻
- B往上走填充A
反走样
有两个方式,一个是提高分辨率,另一个是改进算法,这里当然讲算法喽
简单区域采样(非加权区域采样)
根据面积改变亮度达到反走样效果
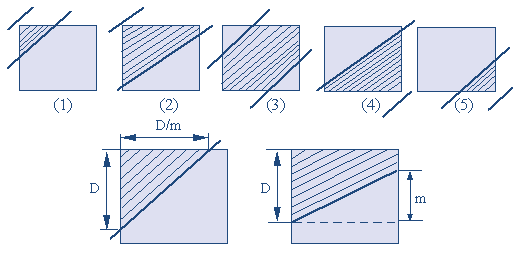
面积计算(m是斜率,像素宽为1)
- 情况(1)(5)阴影面积为: D 2 2 m \frac{D^2}{2m} 2mD2
- 情况(2)(4)阴影面积为: D − m 2 D - \frac{m}{2} D−2m
- 情况(3)阴影面积为: 1 − D 2 m 1-\frac{D^2}{m} 1−mD2
上述阴影面积是介于0-1之间的正数,用它乘以象素的最大灰度值,再取整,即可得到象素的显示灰度值。
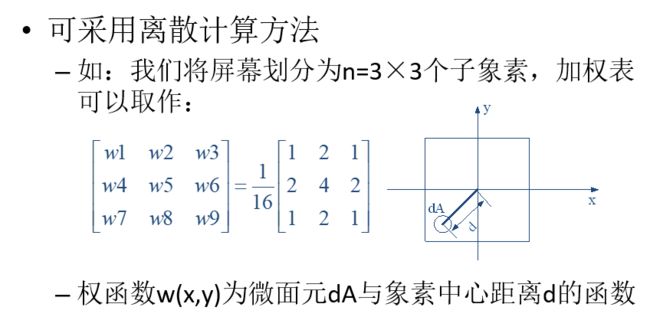
加权区域采样
其实就是在非加权区域采样的基础上加了个权值来表示与中心距离,然后计算灰度的时候要考虑这个权值。

直线和多边形裁剪
编码裁剪
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0分别表示是否上于上边界,是否下于下边界,是否右于右边界,是否左于左边界
- 是为1,否为0

- 若 P 1 P 2 P_1P_2 P1P2完全在窗口内(code1 || code2) = 0, 则“取”
- 若 P 1 P 2 P_1P_2 P1P2明显在窗口外(code1 & code2) ≠ 0, 则“弃”
- 在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理
中点分割裁剪
和编码的区别在于最后一步,不是交点处分为两段,而是中点处,然后不断二分,把完全在窗口外的舍弃,直到精度满足要求。
梁友栋-Barskey算法
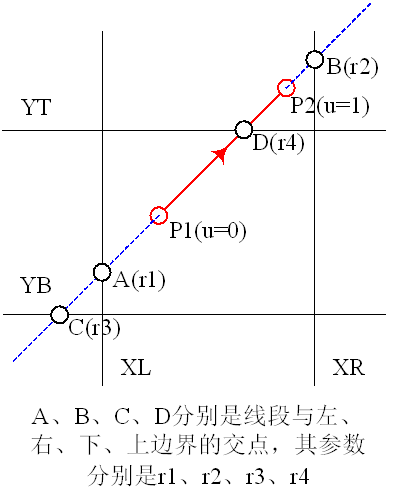
首先,我们将这个线段确定一个方向,然后将线段和窗口延长,得到四个交点,记为 r 1 , r 2 , r 3 , r 4 r1,r2,r3,r4 r1,r2,r3,r4(这也是它们的横坐标)
这样,我们得到两个入边和两个出边(PPT上叫始边和终边)
这样我们要裁剪得到的线段的两个端点的横坐标 u 1 u 2 u_1u_2 u1u2就可以确定了
- u 1 = m a x ( 0 , x 入 边 1 , x 入 边 2 ) u1 = max(0, x_{入边1},x_{入边2}) u1=max(0,x入边1,x入边2)
- u 2 = m i n ( 1 , x 出 边 1 , x 出 边 2 ) u2 = min(1, x_{出边1},x_{出边2}) u2=min(1,x出边1,x出边2)
那么我们要如何确定入边出边呢?
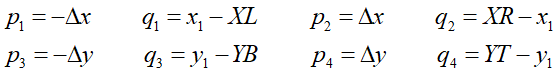
每个交点的横坐标为 r k = q k p k r_k = \frac{q_k}{p_k} rk=pkqk
如果 p k ≠ 0 p_k \neq 0 pk=0
- p k < 0 p_k<0 pk<0 入边
- p k > 0 p_k>0 pk>0 出边
多边形逐边裁剪算法
多边形的各条边的两端点S、P。它们与裁剪线的位置关系只有四种:
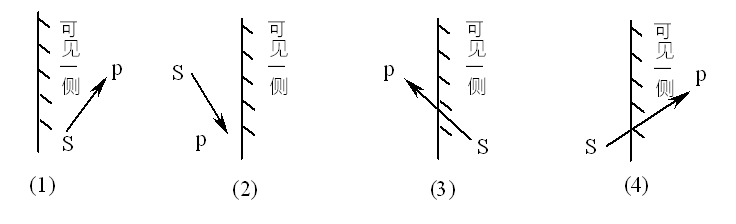
情况(1)仅输出顶点P;
情况(2)输出0个顶点
情况(3)输出线段SP与裁剪线的交点 I
情况(4)输出线段SP与裁剪线的交点 I 和终点 P
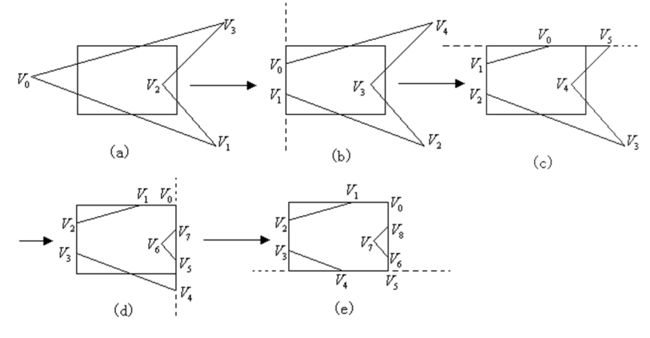
双边裁剪算法
这个我还没实践过,所以直接粘贴下PPT。算法思想的话,PPT上这个够看了。
简单来说,就是我们的裁剪窗口不再是矩形了,而是一个多边形。


算法思想
- 计算主多边形与裁剪多边形的交点
- 如果主多边形与裁剪多边形有交点,则交点成对出现,它们被分为如下两类
- 进点:主多边形边界由此进入裁剪多边形内
- 出点:主多边形边界由此离开裁剪多边形区域
- 跟踪任意一个交点
- 如果为进点,则跟踪主多边形边界
- 如果为出点,则跟踪裁剪多边形边界
- 任选一个没有跟踪过的交点,按上述过程重新搜索,直至所有交点跟踪完毕
- 如果该交点为进点,跟踪主多边形边边界;否则跟踪裁剪多边形边界
- 跟踪多边形边界,每遇到多边形顶点,将其输出到结果多边形顶点表中,直至遇到新的交点
- 将该交点输出到结果多边形顶点表中,并通过连接该交点的双向指针改变跟踪方向(如果上一步跟踪的是主多边形边界,现在改为跟踪裁剪多边形边界;如果上一步跟踪裁剪多边形边界,现在改为跟踪主多边形边界)
- 重复(4)、(5)直至回到起点
消隐
深度缓存算法(Z_Buffer算法)
加入一个深度缓存数组z[m][n]来存最小深度值
加入一个帧缓存数组FB[m][n]来存像素点对应颜色值
每个像素点上放深度最小的多边形的颜色
扫描线算法
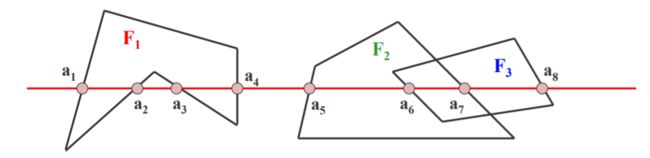
扫描线的交点把这条扫描线分成了若干个区间,每个区间上必然是同样一种颜色
对于有重合的区间,如** a 6 a 7 a_6a_7 a6a7**这个区间,要么显示F2的颜色,要么显示F3的颜色,不会出现颜色的跳跃
如果把扫描线和多边形的这些交点都求出来,对每个区间,只要判断一个像素的要什么颜色,那么整个区间的颜色都解决了,这就是区间扫描线算法的主要思想。
需要的数据结构有很多,比如多边形y桶、有效多边形表APT、边Y桶、有效边表AET,具体这些是啥,看PPT吧
多边形区域排序算法
在规则化图像空间中,将多边形按深度Z值自小至大排序,用前面的可见多边形去切割其后面的多边形,使得最终每一个多边形要么是完全可见,要么完全不可见。
曲线曲面
我这里写得有点点乱,以后有空再修改吧。
Hermite曲线
![]()

Bezier曲线
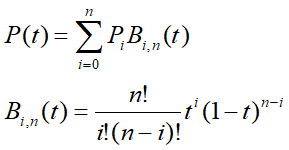
P i P_i Pi是控制点
有n个控制点,那么曲线的阶数就是n-1,计算量巨大
Bezier曲线的性质
- 端点性质 曲线过两端点且与端点相切
- 对称性: 若保持n次Bezier曲线的顶点的位置不变,而把次序颠倒,则曲线保持不变
- 凸包性: 伯恩斯坦多项式各项之和为1。这意味着Bezier曲线各点均落在特征多边形顶点构成的凸包之中
- 几何不变性:曲线的形状仅与特征多边形个顶点的相对位置有关,而与坐标的选择无关
B样条曲线

这个图是PPT上的,和我下面的有些许不同,但实际是一样的。

这个图是我要讲的,下面就逐步来解释
啥是B样条曲线?
整条曲线用一个完整的表达形式,但内在的量是一段一段的,比如一堆的3次曲线拼过去,两条之间满足2次连续
怎么分段呢?

每一段的基函数怎么求?
de Boor-Cox递推定义
只要是k阶(k-1次)的B样条基函数,构造一种递推的公式,由0次构造1次,1次构造2次,2次构造3次…依次类推
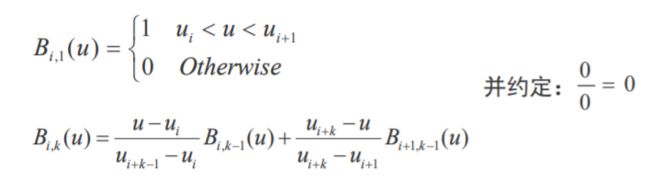
B样条函数定义区间 u ∈ [ u k − 1 , u n + 1 ] u\in[u_{k-1},u_{n+1}] u∈[uk−1,un+1] 是怎么来的?
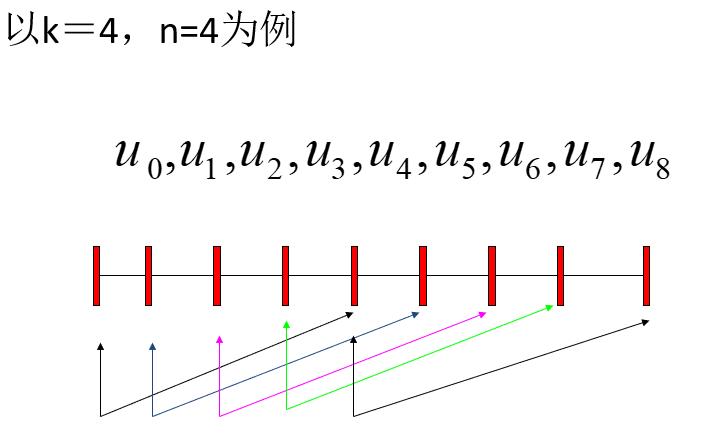

B样条曲线的性质
- 端点性质与连续性
- 当t=0 或 t=1分别代入三次B样条方程得:
P ( 0 ) = 1 / 3 ∗ ( ( p i + p i + 2 ) / 2 + 2 p i + 1 ) P(0)=1/3*((p_i+p_{i+2})/2+2p_{i+1}) P(0)=1/3∗((pi+pi+2)/2+2pi+1)
P ( 1 ) = 1 / 3 ∗ ( ( p i + 1 + p i + 3 ) / 2 + 2 p i + 2 ) P(1)=1/3*((p_{i+1}+p_{i+3})/2+2p_{i+2}) P(1)=1/3∗((pi+1+pi+3)/2+2pi+2)
三次B样条在连接处的一阶导数、二阶导数都是连续的。‘ - 局部性:改变一个控制点的位置,最多影响四个曲线段。由此三次B样条具有改变控制点的位置就可以对B样条局部修改曲线
- 扩展性:增加一个控制点就相应增加一段B样条曲线,而原有曲线不受任何影响
图形变换
平移变换
二维

三维

比例变换
二维

三维
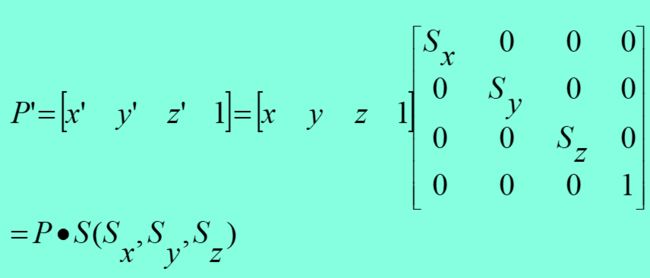
旋转变换
二维
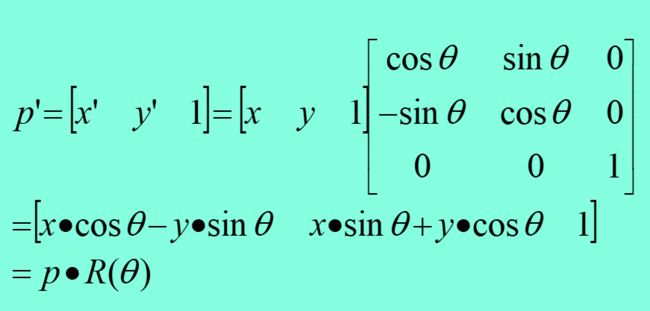
三维
绕z轴旋转
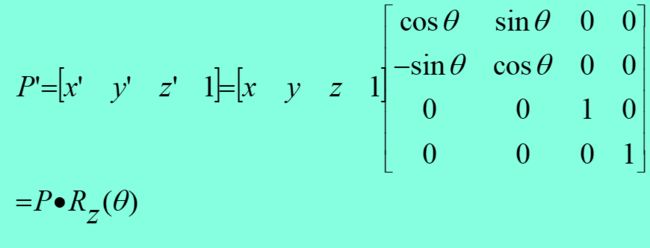
绕x轴旋转
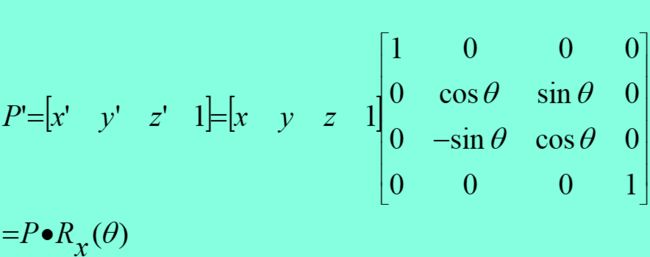
绕y轴旋转
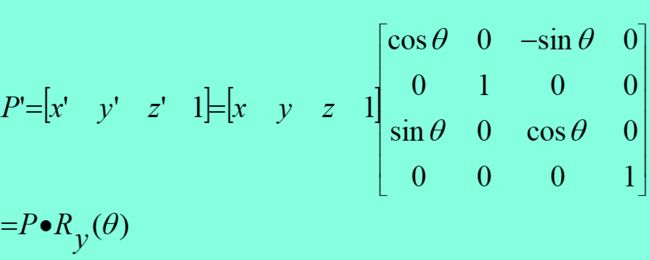
对称变换
错切变换
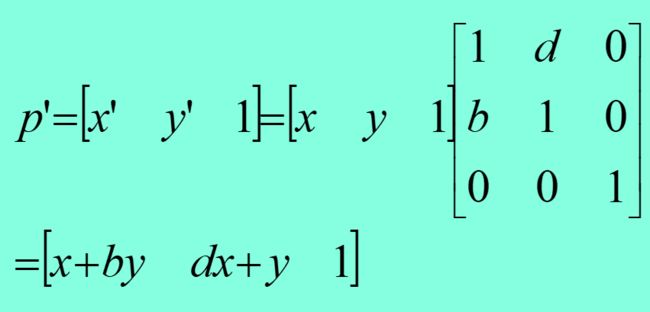
投影变换
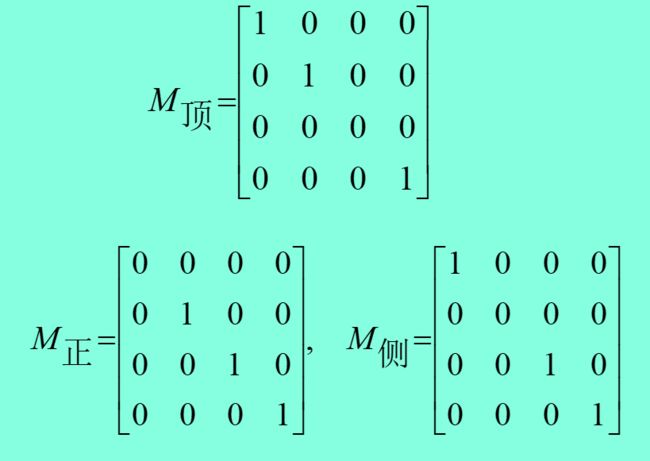
正交平行投影
斜交投影
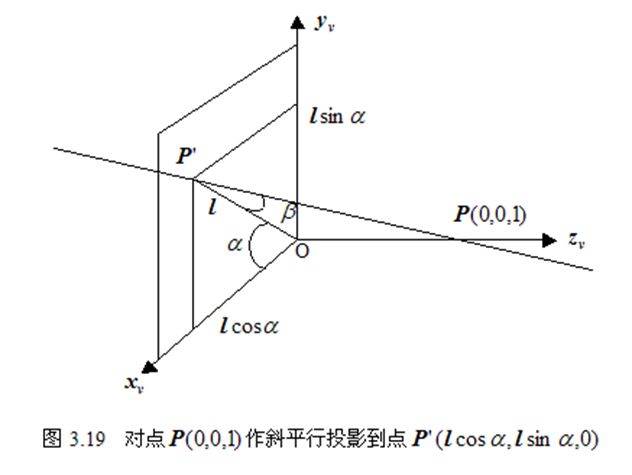
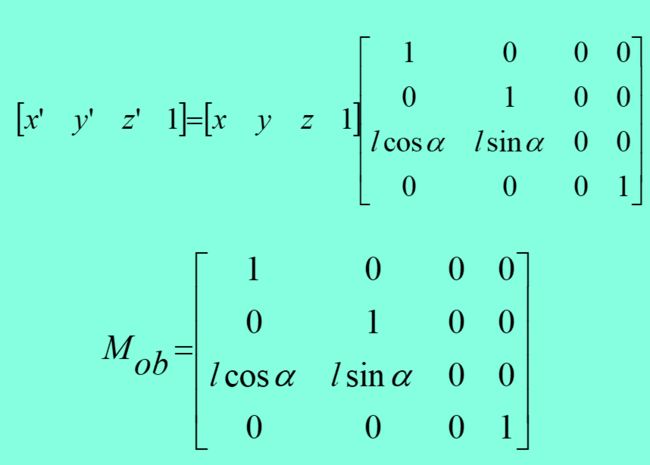
透视投影