FastICA算法
目前比较成熟的线性盲源分离算法有很多,FastICA是其中之一。
1 ICA算法流程
(1) 归一化
首先将观测数据x
归一化,即减去其均值m=E{x}使其具有零均值。这意味着s也是零均值的。
归一化预处理能简化ICA算法,在估计出归一后的混合矩阵A后,将计算出的分离信号s再加上s的均值A-1m。
(2) 白化
在归一化之后,线性变换观测向量x使其各成分不相关且有单位方差,即白化为新向量x',其协方差矩阵等于单位矩阵:E{x'x'T}=I。
一种常用的白化方法对数据协方差进行特征值分解(Eigen-ValueDecomposition,EVD),即E{xxT}=EDET,其中E是E{xxT}特征向量的正交矩阵,D是其特征值的对角矩阵,D=diag(d1,…,dn)。因而白化操作可写为
x'=ED-1/2ETx
其中D-1/2=diag(d1-1/2,…,dn-1/2)。同理,白化混合矩阵得A',则A‘是正交的。
白化操作能减少待估计的参数。估计矩阵A要估计n2个参数,而估计正交矩阵A'只需估计n(n-1)/2个参数,这大大减小了ICA算法的计算复杂度。
(3) FastICA算法
在讨论了的ICA估计几种目标函数中,实际应用中需要一种最大化目标函数的算法,一种常用的算法就是FastICA算法。这里假设数据已经经过归一化和白化,z'和A’和分别用x和A表示。
首先讨论算法的一次处理过程。FastICA算法基于定点迭代结构的算法,目的是使wTx具有最大非高斯性,其中w是W的一行。采用式J(y) ∝ [E{G(y)} – E{G(v)}]2为目标函数,定义g为非二次函数G的导数。则式G1(u) = 1/a1logcosh(a1u) ,G2(u) = - exp(-u2/2)中函数的导数为
g1(u) = tanh(a1u), g2(u) = u exp(-u2/2)
其中1≦a1≦2为一个合适的常量,通常选a1=1。
E{ xg( w T x)}-β w=0
用牛顿方法解此方程。定义方程左边为F,得到它的雅克比矩阵JF(w)为
JF( w) = E{ xx Tg’( w T x)}- β I上式右边第一项可简化为E{xxTg’(wTx)}≈E{xxT}E{g’(wTx)}= E{g’(wTx)}I,雅克比矩阵变成对角的、可逆的。因此获得近似牛顿迭代:
w+ =w – [E{xg(wTx)}- βw]/[ E{g’(wTx)}- β]
两边同乘β-E{g’(wTx)},进一步简化为w+ =E{xg(wTx)}– E{g’(wTx)}w。
综上,一次FastICA算法的基本形式为:
1)初始化(如随机)向量w;
2)令w+ = E{xg(wTx)} – E{g’(wTx)}w;
3)令w= w+/||w+||;
4)若未收敛,则回到2)。
其中收敛意味着前后两次向量w在同一方向上,即它们的点积为1。
一次FastICA算法能估计出一个独立成分,为了估计出若干个独立成分,需要进行若干次FastICA算法得到向量w1,…,wn。为了防止这些向量收敛在同一个最大值,需要对每次迭代后的输出w1Tx,…,wnTx去相关。
一种简单的方法是Gram-Schmidt-like去相关,即一个接一个地估计独立成分。在估计出p个独立成分w1,…,wp之后,当估计wp+1时先减去先前预测的p个向量的投影wp+1Twjwj,j=1,…,p,然后标准化wp+1,即
1)![]()
2)![]()
有时希望对称去相关,这样所有独立成分都是平等的,这可通过矩阵平方根完成,即
其中W=[w1,…,wn]T,逆平方根(WWT)-1/2通过特征值分解获得,(WWT)-1/2=(FDFT)-1/2=FD-1/2FT。一个很简单的方法是通过如下迭代算法
1)2) 令W= 3/2W – 1/2WWTW
3) 重复2),直至收敛。
2 算法仿真效果
(1)对模拟信号分离
首先用matlab产生4个相互独立的语音信号,分别为正弦曲线、不规则曲线、锯齿形曲线和脉冲噪声,波形如图1所示。然后用一个随机矩阵将它们混合,产生4个混合信号,如图2所示
图2 4个混合信号
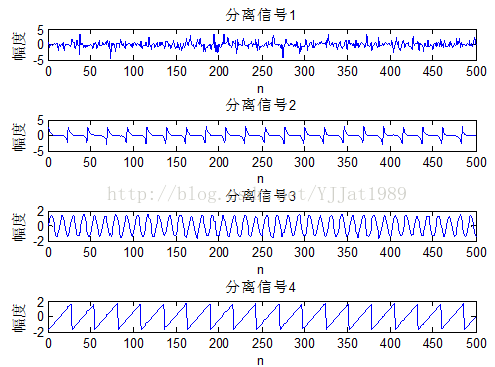
运用FastICA算法对混合信号进行独立成分分析,分离结果如图3所示。
图3 独立成分分析结果
比较图3和图1可以看出,FastICA算法成功分离出了4种独立信号,效果明显。唯一不同之处在于分离顺序是不确定的,这是线性混合的必然结果。
(2) 声音信号分离
语音信号来自赫尔辛基工业大学官网,分别为警笛声、乐器声、男语音和女语音,波形如图4所示。然后对其进行线性混合,得到4个混合声音信号,波形如图5所示。

图4 4个声音信号
图5 4个混合信号
运用FastICA算法对混合语音信号进行分离,分离结果如图6所示。
图6 盲源分离语音信号
比较图6和图4可以看出,FastICA算法成功对4种声音信号进行了分离,而且对警笛声和乐器声的分离效果很好,分离出的人声信号依然存在一些干扰,但是可以很明显分辨出人声。