计算方法：列主元消去法，LU分解法， 雅可比迭代法，高斯塞德尔迭代法 解线性方程（C++）

Matrix.h包括矩阵类Matrix的定义，Matrix.cpp包括该类成员函数的实现，LinearEqu.h包括线性方程类LinearEqu的定义，继承自Matrix类，其中solve()方法为列主元消去法的具体步骤，LU()方法为LU分解法的具体步骤。

Matrix.h（矩阵类头文件）:

//矩阵
class Matrix  
{
public:
	Matrix(int size = 2);
	virtual ~Matrix();
	void setMatrix(const double* values);	//矩阵赋初值
	void displayMatrix() const;	//输出矩阵
	int getSize() const {return size;}		//矩阵大小
	double &element(int i, int j) {return elements[i * size + j];}
	double element(int i, int j) const {return elements[i * size + j];}
private:
	int size;
	double* elements;
};

Matrix.cpp（矩阵类方法实现）:

#include "Matrix.h"
#include
using namespace std;

Matrix::Matrix(int size) : size(size){
	elements = new double[size * size];
}

Matrix::~Matrix(){
	delete[] elements;
}

//设置矩阵
void Matrix::setMatrix(const double* values)
{
	for(int i = 0; i < size * size; i++)
		elements[i] = values[i];	//矩阵元素赋值
}

//显示矩阵
void Matrix::displayMatrix() const{
	cout << "The matrix is:" << endl;
	for(int i = 0; i < size; i++){
		for(int j = 0; j < size; j++)
			cout << element(i, j) << "\t";
		cout << endl;
	}
}

LinearEqu.h（线性方程类头文件）:

#include "Matrix.h"

//线性方程
class LinearEqu : public Matrix
{
public:
	LinearEqu(int size = 2);
	virtual ~LinearEqu();
	void setLinearEqu(const double* a, const double* b);	//方程赋值
	bool solve();	//列主元消去法
bool LU();		//LU分解法
	void displayLinearEqu() const;	//显示方程
	void displaySolution() const;	//显示方程的解
private:
	double* sums;	//方程右端
	double* solution;	//方程的解s

};

LinearEqu.cpp（线性方程类方法实现）:

// LinearEqu.cpp: implementation of the LinearEqu class.
//
//////////////////////////////////////////////////////////////////////

#include "stdafx.h"
#include "LinearEqu.h"
#include 
#include 
#include 
using namespace std;

//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////

LinearEqu::LinearEqu(int size) : Matrix(size)
{
	sums = new double[size];
	solution = new double[size];
}

LinearEqu::~LinearEqu()
{
	delete[] sums;
	delete[] solution;
}

void LinearEqu::setLinearEqu(const double* a, const double* b){
	setMatrix(a);
	for(int i = 0; i < this->getSize(); i++)
		sums[i] = b[i];
}

void LinearEqu::displayLinearEqu() const{
	cout << "The Linear equation is:" << endl;
	for(int i = 0; i < this->getSize(); i++){
		for(int j = 0; j < this->getSize(); j++)
			cout << element(i, j) << "\t";
		cout << sums[i] << endl;
	}
}

void LinearEqu::displaySolution() const{
	cout << "The Result is:" << endl;
	for(int i = 0; i < this->getSize(); i++)
		cout << "x[" << i << "] = " << solution[i] << endl;
}

//交换
inline void swap(double &v1, double &v2){
	double temp = v1;
	v1 = v2;
	v2 = temp;
}

//列主元消去法
bool LinearEqu::solve(){
	int n = this->getSize();
	for(int k = 0; k < n - 1; k++){
		int is;
		double max = 0;
		for(int i = k, j = k; i < n; i++){
			double t = fabs(element(i, j));
			if(t > max){
				max = t;
				is = i;
			}
		}
		if(max == 0){
			return false;
		}
		//交换行
		else{
			if(is != k){
				for(int j = k; j < n; j++)
					swap(element(k, j), element(is, j));
				swap(sums[k], sums[is]);
			}
		}

		//消去
		double major = element(k, k);
		for(i = k + 1; i < n; i++){
			double m = element(i, k) / major;
			for(int j = k; j < n; j++){
				element(i, j) -= element(k, j) * m;
			}
			sums[i] -= sums[k] * m;
		}
	}

	//判断剩下的一个元素是否为0
	double d = element(n - 1, n - 1);
	if(fabs(d) < 1e-15){
		return false;
	}

	//回代过程
	solution[n - 1] = sums[n - 1] / d;
	for(int i = n - 2; i >= 0; i--){
		double t = 0.0;
		for(int j = i + 1; j <= n - 1; j++)
			t += element(i, j) * solution[j];
		solution[i] = (sums[i] - t)/element(i, i);
	}
 	return true;
} 

//LU分解法
bool LinearEqu::LU(){
	int n = this->getSize();
	vector > L(n ,vector(n));
	vector > U(n ,vector(n));
	
	//U第一行赋值
	for(int i = 0; i < n; i++)
		U[0][i] = element(0, i);
	//L第一列赋值
	for(int j = 1; j < n; j++)
		L[j][0] = element(j, 0) / U[0][0];
	//剩余赋值
	for(i = 1; i < n; i++){
		for(j = i; j < n; j++){
			double sum1 = 0;
			for(int k = 0; k < i; k++)
				sum1 += L[i][k] * U[k][j];
			U[i][j] = element(i, j) - sum1;
		}
		for(j = i+1; j < n; j++){
			double sum2 = 0;
			for(int k = 0; k < i; k++)
				sum2 += L[j][k] * U[k][i];
			L[j][i] = (element(j, i) - sum2) / U[i][i];
		}
	}

	vector Y(n);
	Y[0] = sums[0];
	for (i = 1; i= 0; i--)
    {
        double sum4 = 0;
        for (int k = i + 1; kgetSize();
	int i,j;
	vector x1(n);
	vector x2(n);
	vector b(n);
	vector > a(n ,vector(n));
	double sum, max=INT_MAX, eps=1e-5, count=0;
	for(i = 0; i < n; i++){
		b[i] = sums[i] / element(i, i);
		for(j = 0; j < n; j++){
			a[i][j] = - element(i, j) / element(i, i);
		}
		a[i][i] = 0;
	}
	while(max > eps){
		for(i = 0; i < n; i++){
			sum = 0;
			for(j = 0; j < n; j++)
				sum += a[i][j] * x1[j];
			x2[i]  = sum + b[i];
			solution[i] = x2[i];
		}
		max = fabs(x1[0] - x2[0]);
		for(i = 1; i < n; i++)
			if(max < fabs(x1[i] - x2[i]))
				max = fabs(x1[i] - x2[i]);
		for(i = 0; i < n; i++){
			x1[i] = x2[i];
		}
		count++;
	}
	cout << "经过" << count << "次迭代" << endl;
	return true;
}

//高斯塞德尔迭代法
bool LinearEqu::GS()
{
	int n = this->getSize();
	int i,j,k;
	vector x1(n);
	vector x2(n);
	vector b(n);
	vector > a(n ,vector(n));
	double sum, max=INT_MAX, eps=1e-5, count=0;
	for(i = 0; i < n; i++){
		b[i] = sums[i] / element(i, i);
		for(j = 0; j < n; j++){
			a[i][j] = - element(i, j) / element(i, i);
		}
		a[i][i] = 0;
	}
	while(max > eps){
		for(i = 0; i < n; i++){
			sum = 0;
			for(j = 0; j < i; j++){
				sum += a[i][j] * x2[j];
			}
			for(k = j; k < n; k++){
				sum += a[i][k] * x1[k];
			}
			x2[i]  = sum + b[i];
			solution[i] = x2[i];
		}
		max = fabs(x1[0] - x2[0]);
		for(i = 1; i < n; i++)
			if(max < fabs(x1[i] - x2[i]))
				max = fabs(x1[i] - x2[i]);
		for(i = 0; i < n; i++){
			x1[i] = x2[i];
		}
		count++;
	}
	cout << "经过" << count << "次迭代" << endl;
	return true;
}

Main.cpp（主函数）:

// 列主元消去.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include "LinearEqu.h"
#include
using namespace std;

int main(int argc, char* argv[])
{
	double a[] = {
		12, -3, 3,
		-18, 3, -1,
		1, 1, 1};
	double b[] = {15, -15, 6};	//方程右端
	LinearEqu equ(3);
	equ.setLinearEqu(a,b);
	equ.displayLinearEqu();
	cout << endl;
	
	//列主元消去法：
	cout << "列主元消去法：" << endl;
	if(equ.solve())
		equ.displaySolution();
	else
		cout << "Fail" << endl;
	cout << endl;

	//LU分解法
	cout << "LU分解法：" << endl;
	if(equ.LU())
		equ.displaySolution();
	else
		cout << "Fail" << endl;
	cout << endl;
	
	double c[] = {
		10, -1, -2,
		-1, 10, -2,
		-1, -1, 5};
	double d[] = {72, 83, 42};
	LinearEqu equ2(3);
	equ2.setLinearEqu(c,d);
	equ2.displayLinearEqu();
	cout << endl;
	
	//雅可比迭代法
	cout << "雅可比迭代法:" << endl;
	if(equ2.Jacobi())
		equ2.displaySolution();
	else
		cout << "Fail" << endl;
	cout << endl;

	//高斯塞德尔迭代法
	cout << "高斯塞德尔迭代法:" << endl;
	if(equ2.GS())
		equ2.displaySolution();
	else
		cout << "Fail" << endl;

	return 0;
}

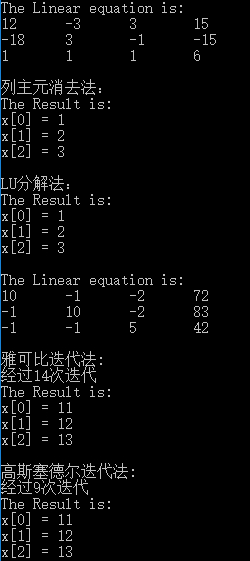
运行结果：