PID控制算法+倒立摆控制应用
一、位式控制算法
传统的控制算法采用位式控制算法:
特点
- 位式控制算法输出信号只有H\L两种状态
- 算法输出信号OUT的依据:
二位式:
Pv < Sv -->H
pV >=Sv -->L- 只考察控制对象当前的状态值
位式控制算法算法的缺点在于只考察控制对象当前传感器传回来的值与目标值之间有无偏差,并且只有两种状态导致无法精确控制在目标值上。
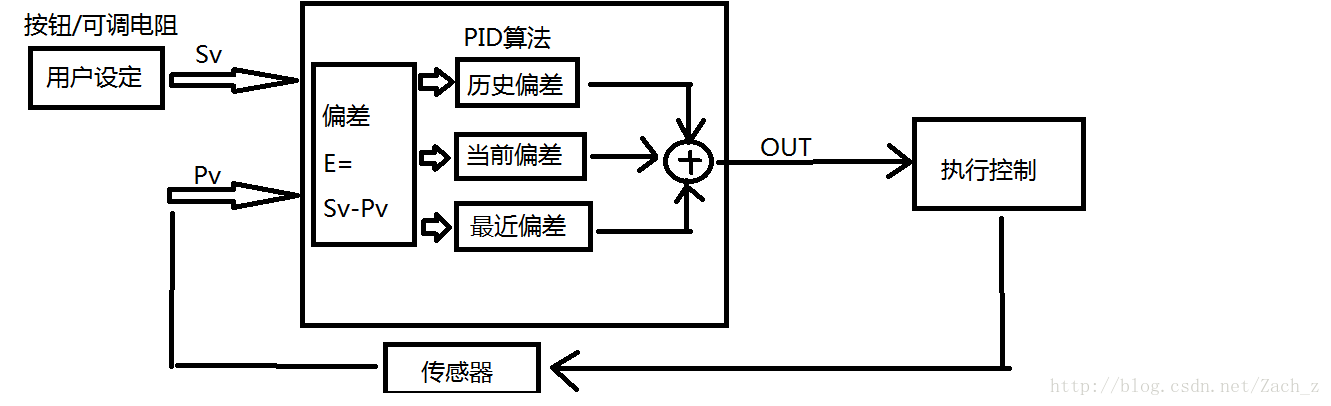
二、 PID控制算法
算法分析
1. 开机以来,传感器采样点的数据序列
X1,X2,X3 ······ ,Xk-2,Xk-1,Xk2. 分析采样点的数据序列:可以挖掘3方面的信息
2.1 比例控制
基本思想: 只关心现在有无偏差
Ek = Sv - Xk
EK>0; 当前控制未达标
Ek=0; 当前控制达标
Ek<0; 当前控制超标
POUT = Kp * Ek --------- 比例控制(输出信号大小与目前的误差值成比例)比例控制有缺陷,当Ek=0时,便不控制,但周围环境会使系统有变化,控制不会很精准,可以加上一个常数 POUT=kp*Ek+OUT1
2.2 积分控制
基本思想: 根据历史状态来输出信号
把每一个采样点与目标值进行比较,得到历史偏差序列:
E1,E2,E3 ······ Ek-2,Ek-1,Ek
Sk = E1+E2+E3+······Ek-2+Ek-1+Ek(每一项都可正可负,不会无限大)
Sk>0; 所有偏差之和为正,控制总体偏低,未达标 (输出信号应该加强)
Sk=0;
Sk<0; 所有偏差之和为负,控制总体偏高,超标 (输出信号减弱)
IOUT = Ki * Sk --------- 积分控制积分控制,当历史数据为0,认为现在没有问题,不控制,陷入失控,可以加上一个常数 IOUT = Ki*Sk+OUT2
2.3 微分控制
基本思想: 只关心偏差有没有变化趋势
最近两次的偏差相减
Dk = Ek -Ek-1 (得到两次变化的偏差之差)
Dk>0; 这一次的偏差值大于上一次,越来越偏离我们的目标,偏差有增大趋势
Dk=0; 前一次采样和后一次采样之间的变化没有产生变化
Dk<0;
DOUT = Kd * Dk ----------微分控制同理,等于0时前一次采样和后一次采样之间的变化没有产生变化,为了在变化率没有改变的情况下系统不至于失控 DOUT = Kd*Dk+OUT3
三、倒立摆角度环与位置环
1. 角度环
1.1 算法设计
通过STM32用adc采集角位移传感器(WDD35D-4导电塑料电位器)的值,由之前学到的PID控制算法理论可以得出,通过控制电机的转动与PWM的值来使倒立摆达到我们所希望的角度。
根据所需要的系统要求,只需要让其达到所期望的角度,历史的差值对其影响并不大,所以只需要PD调节即可完成所需。
算法代码如下:
int balance(float Angle)//倾角PD控制
{
float Bias;//倾角偏差
static float Last_Bias,D_Bias;//PID相关变量
int balance;//PWM返回值
Bias=Angle-ZHONGZHI;//求出平衡的角度中值,ZHONGZHI即数直起来的ad值
D_Bias=Bias-Last_Bias;//求出偏差的微分
balance=KP*Bias-D_Bias*KD;//计算倾角PD控制的电机PWM
Last_Bias=Bias;//保持上一次偏差
return balance;
}
1.2 参数整定
KP:逐渐增大KP的值,直到出现反向或者低频抖动的情况
KD:微分控制,控制偏差的变化趋势,实际中便是用来抑制转动惯量(即转动过猛)
2. 位置环
单纯进行角度环的控制,会稳定一段时间,但是最终会朝一个方向运动下去,因此还必须加上位置环的控制
位置环就是尽可能的让转动的轴不要移动,同样采用PD控制,代码如下:
int Position(int Encoder)
{
static float Position_PWM,Last_Position,Position_Bias,Position_Differential;
static float Position_Least;
Position_Least =Encoder-Position_Zero; //===
Position_Bias *=0.8;
Position_Bias += Position_Least*0.2; //===一阶低通滤波器
Position_Differential=Position_Bias-Last_Position;
Last_Position=Position_Bias;
Position_PWM=Position_Bias*Position_KP+Position_Differential*Position_KD; //===速度控制
return Position_PWM;
}低通滤波的作用是降低位置控制对角度控制的影响,毕竟角度控制是主要的,而位置控制是会对角度控制造成影响,尽可能消除这一影响