【模型评估】ROC曲线和sklearn实战

ROC曲线

同一个问题可以有多种解决方法，如何选择最优的解决方法呢？这里介绍模型评价标准之ROC曲线。
ROC 曲线则是研究学习器泛化性能的。
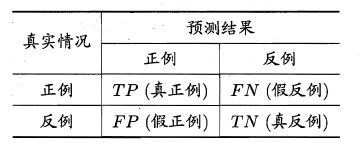
ROC 曲线的纵轴是"真正例率" (True Positive Rate，简称TPR) ，横轴是"假正例率" (False PositiveRate，简称FPR)，两者分别定义为：
$TPR=\frac{TP}{(TP+FN)}$
$FPT=\frac{FP}{(TP+FP)}$
¹
AUC (Area Under ROC Curve) 是ROC 曲线下的面积。若一个学习器的ROC 曲线被另一个学习器的曲线完全"包住"， 则可断言后者的性能优于前者，或者说AUC越大，性能越好。

ROC参数

参数解释，见²

sklearn.metrics.roc_curve
fpr, tpr, thresholds=
sklearn.metrics.roc_curve(y_true,y_score,pos_label=None,sample_weight=None,
drop_intermediate=True)

ROC实例

实例修改自[3]，感谢博主。通过实践发现ROC曲线在特征较多的时候，可以画出较平滑的曲线。对于特征很多的例子，roc曲线在选择模型时，很有用。roc曲线貌似针对2分类问题，多分类问题可能需要控制变量法，将一个类设为正类，其余设为负类。
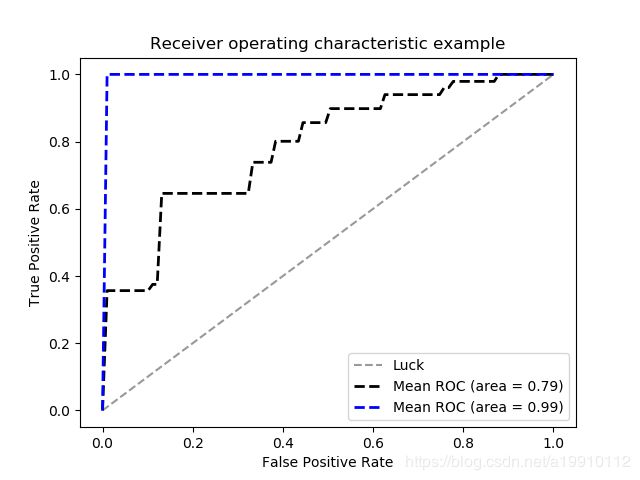
该实例比较了决策树和逻辑回归在iris数据集上的第一类和第二类的分类效果。实验表明：决策树的效果比逻辑回归好！

导入需要的包
from sklearn.model_selection import StratifiedKFold这个包是将数据分层采样，感觉好厉害的样子！

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn import tree

开始数据处理

iris = datasets.load_iris()
X = iris.data
y = iris.target
X, y = X[y != 2], y[y != 2]  # 去掉了label为2，label只能二分，才可以。
n_samples, n_features = X.shape
# 增加噪声特征
random_state = np.random.RandomState(0)
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]

cv = StratifiedKFold(n_splits=6)  # 导入该模型，后面将数据划分6份
classifier = LogisticRegression(random_state=0, solver='newton-cg', multi_class='multinomial')
classifier_dec = tree.DecisionTreeClassifier()
    # svm.SVC(kernel='linear', probability=True, random_state=random_state)  # SVC模型 可以换作AdaBoost模型试试

# 画平均ROC曲线的两个参数
mean_tpr = 0.0  # 用来记录画平均ROC曲线的信息
mean_fpr = np.linspace(0, 1, 100)
mean_tpr_dec = 0.0  # 用来记录画平均ROC曲线的信息
mean_fpr_dec = np.linspace(0, 1, 100)
cnt = 0
for i, (train, test) in enumerate(cv.split(X, y)):  # 利用模型划分数据集和目标变量 为一一对应的下标
    cnt += 1
    probas_ = classifier.fit(X[train], y[train]).predict_proba(X[test])  # 训练模型后预测每条样本得到两种结果的概率
    fpr, tpr, thresholds = roc_curve(y[test], probas_[:, 1])  # 该函数得到伪正例、真正例、阈值，这里只使用前两个

    mean_tpr += np.interp(mean_fpr, fpr, tpr)  # 插值函数 interp(x坐标,每次x增加距离,y坐标)  累计每次循环的总值后面求平均值
    mean_tpr[0] = 0.0  # 将第一个真正例=0 以0为起点

    roc_auc = auc(fpr, tpr)  # 求auc面积

    probas_dec = classifier_dec.fit(X[train], y[train]).predict_proba(X[test])  # 训练模型后预测每条样本得到两种结果的概率
    fpr_dec, tpr_dec, thresholds_dec = roc_curve(y[test], probas_dec[:, 1])  # 该函数得到伪正例、真正例、阈值，这里只使用前两个

    mean_tpr_dec += np.interp(mean_fpr_dec, fpr_dec, tpr_dec)  # 插值函数 interp(x坐标,每次x增加距离,y坐标)  累计每次循环的总值后面求平均值
    mean_tpr_dec[0] = 0.0  # 将第一个真正例=0 以0为起点

    roc_auc = auc(fpr_dec, tpr_dec)  # 求auc面积
    # plt.plot(fpr, tpr, lw=1, label='ROC fold {0:.2f} (area = {1:.2f})'.format(i, roc_auc))  # 画出当前分割数据的ROC曲线

plt.plot([0, 1], [0, 1], '--', color=(0.6, 0.6, 0.6), label='Luck')  # 画对角线

mean_tpr /= cnt  # 求数组的平均值
mean_tpr[-1] = 1.0  # 坐标最后一个点为（1,1）  以1为终点
mean_auc = auc(mean_fpr, mean_tpr)

plt.plot(mean_fpr, mean_tpr, 'k--', label='Mean ROC (area = {0:.2f})'.format(mean_auc), lw=2)

mean_tpr_dec /= cnt  # 求数组的平均值
mean_tpr_dec[-1] = 1.0  # 坐标最后一个点为（1,1）  以1为终点
mean_auc_dec = auc(mean_fpr_dec, mean_tpr_dec)

plt.plot(mean_fpr_dec, mean_tpr_dec, 'b--', label='Mean ROC (area = {0:.2f})'.format(mean_auc_dec), lw=2)

plt.xlim([-0.05, 1.05])  # 设置x、y轴的上下限，设置宽一点，以免和边缘重合，可以更好的观察图像的整体
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')  # 可以使用中文，但需要导入一些库即字体
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

³
实例修改自[3]，感谢博主

运行结果

如下图所示，表明在该数据集上，决策树的性能要比逻辑回归性能好，原因是蓝色曲线下的面积比黑色曲线下的面积大。

---

1. 截图引用自周志华老师的瓜书 ↩︎

2. https://www.jianshu.com/p/1da84ac7ff03 ↩︎

3. 实例修改自[link]https://blog.csdn.net/qq_36523839/article/details/81915529 ↩︎