领近点梯度下降法、交替方向乘子法、次梯度法使用实例(Python实现)
简述
凸优化会很详细地讲解这三个算法,这个学期刚好有这门课。
这里以期末的大作业的项目中的一个题目作为讲解。
题目
考虑线性测量b=Ax+e,其中b为50维的测量值,A为50*100维的测量矩阵,x为100维的未知稀疏向量且稀疏度为5,e为50维的测量噪声。从b和A中恢复x的一范数规范化最小二乘法模型(任务!!)
m i n ∣ ∣ A x − b ∣ ∣ 2 2 + ( p / 2 ) ∣ ∣ x ∣ ∣ 1 min||Ax-b||_2^2 +(p/2)||x||_1 min∣∣Ax−b∣∣22+(p/2)∣∣x∣∣1
- p为非负的正则化参数。
- 提示:
在本实验中,设x的真值中的非零元素 服从标准正态分布,A中的元素服从标准正态分布,e中的元素服从均值为0,方差为0.1的高斯分布。
要求使用的算法:
- 邻近点梯度下降法
- 交替方向乘子法
- 次梯度法
实验部分
生成数据
generate-data.py- 保存数据到二进制文件中
import numpy as np
import random
ASize = (50, 100)
XSize = 100
A = np.random.normal(0, 1, ASize)
X = np.zeros(XSize)
e = np.random.normal(0, 0.1, 50)
XIndex = random.sample(list(range(XSize)), 5) # 5 稀疏度
for xi in XIndex:
X[xi] = np.random.randn()
b = np.dot(A, X) + e
np.save("A.npy", A)
np.save("X.npy", X)
np.save("b.npy", b)
邻近点梯度下降法
m i n f 0 ( x ) = s ( x ) + r ( x ) min f_0(x) = s(x) + r(x) minf0(x)=s(x)+r(x)
- s为光滑项
- r为非光滑项
算法过程:
x k + 1 2 = x k − α ∗ ∇ s ( x k ) x k + 1 = a r g m i n x r ( x ) + 1 2 ∗ α ∣ ∣ x − x k + 1 2 ∣ ∣ 2 x^{k+\frac{1}{2} } = x^k - \alpha * \nabla{s(x^k)} \\ x^{k+1} = argmin_x{r(x) +\frac{1}{2*\alpha} || x-x^{k+\frac{1}{2}}||^2} xk+21=xk−α∗∇s(xk)xk+1=argminxr(x)+2∗α1∣∣x−xk+21∣∣2
解析:
这一问本质上就是Lasso的邻近点梯度下降问题。
代入之前的算法过程,得到下面的结果(相比于原来的Lasso简单的变下就好了~)
x k + 1 2 = x k − 2 ∗ α ∗ A T ( A x k − b ) x k + 1 = a r g m i n x { ( p 2 ) ∣ ∣ x ∣ ∣ 1 + 1 2 ∗ α ∣ ∣ x − x k + 1 2 ∣ ∣ 2 } x^{k+\frac{1}{2} } = x^k - 2* \alpha * A^T(Ax^k-b) \\ x^{k+1} = argmin_x{ \{(\frac{p}{2})||x||_1+\frac{1}{2*\alpha} || x-x^{k+\frac{1}{2}}||^2} \} xk+21=xk−2∗α∗AT(Axk−b)xk+1=argminx{(2p)∣∣x∣∣1+2∗α1∣∣x−xk+21∣∣2}
- 求解argmin的方法–软门限法
关于光滑的部分,直接求导,在不光滑的部分,就求次梯度。
然后关于每个分量部分不进行。可以参照代码中的片段,在中间就为0,在区间之外就是对应的一个正数~
实现领近点梯度法
import numpy as np
A = np.load('A.npy')
b = np.load('b.npy')
X = np.load('X.npy')
ASize = (50, 100)
BSize = 50
XSize = 100
alpha = 0.001
P_half = 0.01
Xk = np.zeros(XSize)
zero = np.zeros(XSize)
while True:
Xk_half = Xk - alpha * np.dot(A.T, np.dot(A, Xk) - b)
# 软门限算子
Xk_new = zero.copy()
for i in range(XSize):
if Xk_half[i] < - alpha * P_half:
Xk_new[i] = Xk_half[i] + alpha * P_half
elif Xk_half[i] > alpha * P_half:
Xk_new[i] = Xk_half[i] - alpha * P_half
if np.linalg.norm(Xk_new - Xk, ord=2) < 1e-5:
break
else:
Xk = Xk_new.copy()
print(Xk)
print(X)
附加上画图的代码
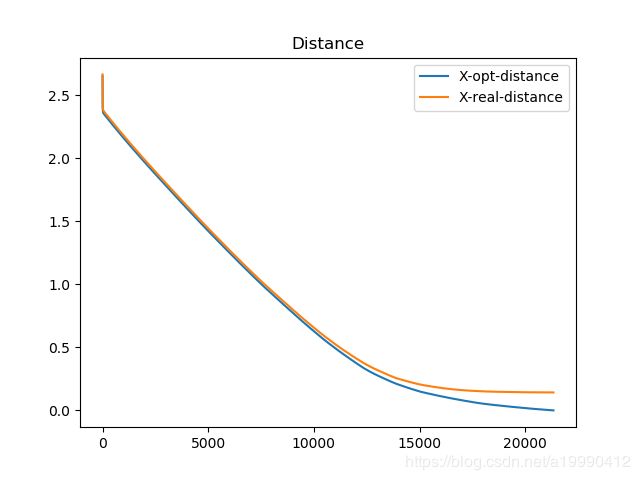
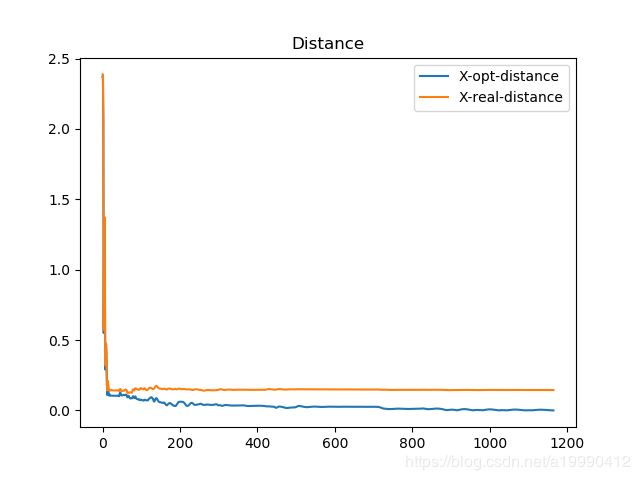
- 蓝色的是算法最优值的距离(最终的收敛点的距离)
- 黄色的是预测的真实值的距离(一开始生成的数据)
- 距离都用的是二范数
import matplotlib.pyplot as plt
import numpy as np
A = np.load('A.npy')
b = np.load('b.npy')
X = np.load('X.npy')
ASize = (50, 100)
BSize = 50
XSize = 100
alpha = 0.005
P_half = 0.01
Xk = np.zeros(XSize)
zero = np.zeros(XSize)
X_opt_dst_steps = []
X_dst_steps = []
while True:
Xk_half = Xk - alpha * np.dot(A.T, np.dot(A, Xk) - b)
# 软门限算子
Xk_new = zero.copy()
for i in range(XSize):
if Xk_half[i] < - alpha * P_half:
Xk_new[i] = Xk_half[i] + alpha * P_half
elif Xk_half[i] > alpha * P_half:
Xk_new[i] = Xk_half[i] - alpha * P_half
X_dst_steps.append(np.linalg.norm(Xk_new - X, ord=2))
X_opt_dst_steps.append(Xk_new)
if np.linalg.norm(Xk_new - Xk, ord=2) < 1e-5:
break
else:
Xk = Xk_new.copy()
print(Xk)
print(X)
X_opt = X_opt_dst_steps[-1]
for i, data in enumerate(X_opt_dst_steps):
X_opt_dst_steps[i] = np.linalg.norm(data - X_opt, ord=2)
plt.title("Distance")
plt.plot(X_opt_dst_steps, label='X-opt-distance')
plt.plot(X_dst_steps, label='X-real-distance')
plt.legend()
plt.show()
交替方向乘子法
m i n f 1 ( x ) + f 2 ( y ) s . t . A x + B y = d min f_1(x)+f_2(y) \\ s.t. Ax+By=d minf1(x)+f2(y)s.t.Ax+By=d
算法过程:
( x k + 1 , y k + 1 ) = a r g m i n x , y { L c ( x , y , v k ) } v k + 1 = v k + c ( A x k + 1 + B y k + 1 ) (x^{k+1}, y^{k+1}) = argmin_{x, y} \{L_c(x, y, v^k)\} \\ v^{k+1} =v^k +c(Ax^{k+1} + B y^{k+1}) (xk+1,yk+1)=argminx,y{Lc(x,y,vk)}vk+1=vk+c(Axk+1+Byk+1)
第一步中有交叉项的话,可以类似的换成下面的方式
x k + 1 = a r g m i n x { L c ( x , y k , v k ) } y k + 1 = a r g m i n y { L c ( x k + 1 , y , v k ) } v k + 1 = v k + c ( A x k + 1 + B y k + 1 ) x^{k+1}= argmin_x \{L_c(x, y^k, v^k)\} \\ y^{k+1}= argmin_y \{L_c(x^{k+1}, y, v^k)\} \\ v^{k+1} =v^k +c(Ax^{k+1} + B y^{k+1}) xk+1=argminx{Lc(x,yk,vk)}yk+1=argminy{Lc(xk+1,y,vk)}vk+1=vk+c(Axk+1+Byk+1)
上面说了,这次的问题是一个Lasso问题。
为了使用ADMM算法,这里引入一个新的变元 Z Z Z
所以一致性约束,就变成了 X − Z = 0 X-Z=0 X−Z=0
- L c ( x , v ) Lc(x, v) Lc(x,v) 出自于 增广拉格朗日算法中所提出的增广拉格朗日函数(augmented lagrangian function)
L c ( x , v ) = f 0 ( x ) + < v , A x − b > + c 2 ∣ ∣ A x − b ∣ ∣ 2 2 L c ( x , v ) = L ( x , v ) + c 2 ∣ ∣ A x − b ∣ ∣ 2 2 Lc(x, v) = f_0(x) + <v, Ax-b> + \frac{c}{2} ||Ax-b||_2^2\\ Lc(x, v) = L(x, v) + \frac{c}{2} ||Ax-b||_2^2 Lc(x,v)=f0(x)+<v,Ax−b>+2c∣∣Ax−b∣∣22Lc(x,v)=L(x,v)+2c∣∣Ax−b∣∣22
也就是在拉格朗日函数的基础上,在加上一个二范数作为penalty。
- 其中 c是一个常数(c>0)
对于这道题目,具体为:
L c ( x , z , v ) = ∣ ∣ b − A x ∣ ∣ 2 2 + < v , z − x > + p 2 ∣ ∣ z ∣ ∣ 1 + c 2 ∣ ∣ z − x ∣ ∣ 2 2 Lc(x, z,v) = ||b-Ax||^2_2 + <v, z-x> + \frac{p}{2}||z||_1 + \frac{c}{2} ||z-x||^2_2 Lc(x,z,v)=∣∣b−Ax∣∣22+<v,z−x>+2p∣∣z∣∣1+2c∣∣z−x∣∣22
代入之后,有(做适当地化简),
x k + 1 = a r g m i n x { ∣ ∣ b − A x ∣ ∣ 2 2 − < v k , x > + c 2 ∣ ∣ x − z k ∣ ∣ 2 2 } z k + 1 = a r g m i n z { p 2 ∣ ∣ z ∣ ∣ 1 + < v k , z > + c 2 ∣ ∣ x k + 1 − z ∣ ∣ 2 2 } v k + 1 = v k + c ( z k + 1 − x k + 1 ) x^{k+1} = argmin_x\{||b-Ax||^2_2-<v^k, x> + \frac{c}{2}||x-z^k||^2_2\} \\ z^{k+1} = argmin_z\{\frac{p}{2} ||z||_1+<v^k, z> + \frac{c}{2}||x^{k+1}-z||^2_2\} \\ v^{k+1} = v^k +c(z^{k+1}-x^{k+1}) xk+1=argminx{∣∣b−Ax∣∣22−<vk,x>+2c∣∣x−zk∣∣22}zk+1=argminz{2p∣∣z∣∣1+<vk,z>+2c∣∣xk+1−z∣∣22}vk+1=vk+c(zk+1−xk+1)
当然,我们注意到,x的更新的话,可以直接给出结果(因为是光滑的),通过矩阵求导,我们可以得到。
x k + 1 = z k + v k + 2 A T b 2 A T ∗ A + c ∗ I x^{k+1} = \frac{z^k+v^k+2A^Tb}{2A^T*A + c*I} xk+1=2AT∗A+c∗Izk+vk+2ATb
而z的计算也可以再做一次变换,
z k + 1 = a r g m i n z { p 2 ∣ ∣ z ∣ ∣ 1 + c 2 ∣ ∣ z − x k + 1 + v k c ∣ ∣ 2 2 } z^{k+1} = argmin_z\{\frac{p}{2} ||z||_1+ \frac{c}{2}||z-x^{k+1} +\frac{v^k}{c}||^2_2\} zk+1=argminz{2p∣∣z∣∣1+2c∣∣z−xk+1+cvk∣∣22}
这个就用软门限的方式来进行求解。
同样关于 z i z_i zi 的正负性做分类。然后把x和v作为一个整体看,就是跟之前的软门限一模一样的了~
import matplotlib.pyplot as plt
import numpy as np
A = np.load('A.npy')
b = np.load('b.npy')
X = np.load('X.npy')
ASize = (50, 100)
BSize = 50
XSize = 100
P_half = 0.01
c = 0.005
Xk = np.zeros(XSize)
Zk = np.zeros(XSize)
Vk = np.zeros(XSize)
X_opt_dst_steps = []
X_dst_steps = []
while True:
Xk_new = np.dot(
np.linalg.inv(np.dot(A.T, A) + c * np.eye(XSize, XSize)),
c*Zk + Vk + np.dot(A.T, b)
)
# 软门限算子
Zk_new = np.zeros(XSize)
for i in range(XSize):
if Xk_new[i] - Vk[i] / c < - P_half / c:
Zk_new[i] = Xk_new[i] - Vk[i] / c + P_half / c
elif Xk_new[i] - Vk[i] / c > P_half / c:
Zk_new[i] = Xk_new[i] - Vk[i] / c - P_half / c
Vk_new = Vk + c * (Zk_new - Xk_new)
# print(np.linalg.norm(Xk_new - Xk, ord=2))
X_dst_steps.append(np.linalg.norm(Xk_new - X, ord=2))
X_opt_dst_steps.append(Xk_new)
if np.linalg.norm(Xk_new - Xk, ord=2) < 1e-5:
break
else:
Xk = Xk_new.copy()
Zk = Zk_new.copy()
Vk = Vk_new.copy()
print(Xk)
print(X)
X_opt = X_opt_dst_steps[-1]
for i, data in enumerate(X_opt_dst_steps):
X_opt_dst_steps[i] = np.linalg.norm(data - X_opt, ord=2)
plt.title("Distance")
plt.plot(X_opt_dst_steps, label='X-opt-distance')
plt.plot(X_dst_steps, label='X-real-distance')
plt.legend()
plt.show()
生成的图
次梯度法
x k + 1 = x k − α k g 0 ( x k ) x^{k+1} = x^k - \alpha^kg_0(x^k) xk+1=xk−αkg0(xk)
其中 g 0 ( x ) g_0(x) g0(x) 为 f 0 ( x ) f_0(x) f0(x)的次梯度。
对于这个问题其实分成简单,对于一范数来说,其实次梯度就是我们之前说的软门限算法。
这里重新描述一下:
- x不为0的情况下,为符号函数
- x为0的情况下,为[-1, 1]上的任意数
然后前半部分,就是用正常的梯度了。
实现 + 效果
import matplotlib.pyplot as plt
import numpy as np
A = np.load('A.npy')
b = np.load('b.npy')
X = np.load('X.npy')
def g_right(x):
Xnew = x.copy()
for i, data in enumerate(x):
if data == 0:
Xnew[i] = 2 * np.random.random() - 1
else:
Xnew[i] = np.sign(x[i])
return Xnew
ASize = (50, 100)
BSize = 50
XSize = 100
alpha = 0.001
p_half = 0.001
alphak = alpha
i = 0
g = lambda x: 2 * np.dot(A.T, (np.dot(A, x) - b)) + p_half * g_right(x)
Xk = np.zeros(XSize)
X_opt_dst_steps = []
X_dst_steps = []
while True:
Xk_new = Xk - alphak * g(Xk)
alphak = alpha / (i + 1)
i += 1
X_dst_steps.append(np.linalg.norm(Xk_new - X, ord=2))
X_opt_dst_steps.append(Xk_new)
print(np.linalg.norm(Xk_new - Xk, ord=2))
if np.linalg.norm(Xk_new - Xk, ord=2) < 1e-5:
break
else:
Xk = Xk_new.copy()
print(Xk)
print(X)
X_opt = X_opt_dst_steps[-1]
for i, data in enumerate(X_opt_dst_steps):
X_opt_dst_steps[i] = np.linalg.norm(data - X_opt, ord=2)
plt.title("Distance")
plt.plot(X_opt_dst_steps, label='X-opt-distance')
plt.plot(X_dst_steps, label='X-real-distance')
plt.legend()
plt.show()