【笔试代码题记录】20190815/17/18 360/腾讯/小红书
文章目录
- 360笔试题
- 1. 正方体的表面积
- 2. m进制加法
- 腾讯笔试题
- 1. 比较简单的滑动窗口
- 2. 拆零件
- 3. 杂货店冰淇淋个数
- 4. 飞机航线
- 5. n*3的网格求最高得分
- 小红书笔试题
- 1. 字符串倒序(剑指offer59)
- 2. leetcode198 抢劫犯(重要)
- 3.击败魔物(重要)
360笔试题
1. 正方体的表面积
给个二维数组,数组值代表当前位置的正方体(边长为1)个数,求表面积
leetcode 892 原题 https://leetcode.com/problems/surface-area-of-3d-shapes/
class Solution(object):
def surfaceArea(self, grid):
n, res = len(grid), 0
for i in range(n):
for j in range(n):
if grid[i][j]: res += 2 + grid[i][j] * 4
if i:
res -= min(grid[i][j], grid[i - 1][j]) * 2
if j :
res -= min(grid[i][j], grid[i][j - 1]) * 2
return res
2. m进制加法
两个m进制数都有n位,调整数字顺序,每位分别对应相加取模,得到最大的返回值 。
例如:给定两个数[4,4,1,1,1]和[4,3,0,1,2],都是5进制的,通过调整顺序,得到最大的和为 [4, 4, 3, 3, 2]
(解释:将[4,4,1,1,1]调整为[1,4,1,4,1],将[4,3,0,1,2]调整为[3,0,2,4,1],相加并取模可以得到最大值[4, 4, 3, 3, 2])
解法(递归):【参考】
例如m=5(五进制),最大数字分别为4,3,2,1,0,两个数字为[4,4,1,1,1],[4,3,0,1,2]
-
首先尝试构造4,求出第一个数[4,4,1,1,1]的对应数放入数组 count_0 ,即为[0,0,3,3,3], count_1 = [4,3,0,1,2],找这两个数组的重合数字为0,3,因而递归两个数字变成了[4,1,1],[4,1,2])
-
尝试构造3,求出第一个数[4,1,1]的对应数放入数组 count_0 ,即为[4,2,2],这个地方有个技巧,需判断元素是否大于3, count_1 = [4,1,2],找这两个数组的重合数字为4,2,因而递归两个数字变成了[1],[1]
-
尝试构造2,1+1 = 2,此时递归两个数字变成了[],[]。以此类推
-
递归的结束条件为:两个数字的长度为0。
import copy
def func(nums, m, num): # nums里面存放的是两个数组,m表示m进制,num表示正在凑的数字
res = []
count_0, count_1 = [], copy.deepcopy(nums[1]) # count_0存的是第一个数字的“差值”,count_1直接存第二个数
if len(count_1) == 0: # 递归终止条件
return []
for i in range(len(nums[1])):
if nums[0][i] <= num: # 需判断元素是否大于num
count_0.append(num - nums[0][i]) # 直接相加的值
else: # 相加之后-模运算的值
count_0.append(num + m - nums[0][i])
for i in range(len(nums[1])): # 查询数组里面相同的数字,找到之后赋值为-1
if nums[1][i] in count_0:
res.append(num)
count_0[i] = -1
count_1[i] = -1
# 返回已经删减相同元素的原数组
count_0 = [nums[0][i] for i in range(len(count_0)) if count_0[i] != -1]
count_1 = [nums[1][i] for i in range(len(count_1)) if count_1[i] != -1]
return res + func([count_0, count_1], m, num - 1) # 递归 num-1表示凑下一个更小数字(从4开始,然后凑3,2,1)
nums = [[4,4,1,1,1],[4,3,0,1,2]]
m = 5
print(func(nums, m, m - 1)) # [4, 4, 3, 3, 2]
腾讯笔试题
1. 比较简单的滑动窗口
2. 拆零件
3. 杂货店冰淇淋个数
小明开了个店,冰淇淋有 n 个配料, 店里每个配料的 原材料 数量为 wi ,每个 原材料在商店的价格为 vi, 小明有 m 元钱, 问 可以最多做多少冰淇淋 ?
示例数据:
我当时的解法:暴力解法,AC40%,超时。
AC代码思路:二分查找;【参考】
def cost(num, w, v):
price = 0
for i in range(n):
if w[i] > num:
continue
price += v[i]*(num-w[i])
return price
if __name__ == "__main__":
n, m = 3, 10
w, v = [2,5,3], [2,1,3]
l = min(w) # 最少做这么多
r = 1 + m // sum(v) + max(w) # 最多可以做这么多
while l < r:
mid = (l + r + 1) >> 1
if cost(mid, w, v) < m:
l = mid
else:
r = mid - 1
print(l)
牛客AC代码思路:每次取1或者买全部材料做冰淇淋能做多少,不断更新exist数组,【参考】
#coding=utf-8
# 本题为考试多行输入输出规范示例,无需提交,不计分。
import sys
if __name__ == "__main__":
# 读取第一行的n
line = sys.stdin.readline().strip()
# 把每一行的数字分隔后转化成int列表
nm = list(map(int, line.split()))
n = nm[0]
m = nm[1]
line = sys.stdin.readline().strip()
exist = list(map(int, line.split()))
line = sys.stdin.readline().strip()
money = list(map(int, line.split()))
total_money = sum(money)
ans = 0
min_num = min(exist)
ans += min_num
exist_buf = [i - min_num for i in exist]
exist = exist_buf
while m > 0:
min_num = max(1, m // total_money)
ans += min_num
need = [i - min_num for i in exist]
need_money = 0
for i in range(n):
exist_buf[i] = max(exist[i] - min_num, 0)
if need[i] < 0:
need_money += abs(need[i]) * money[i]
exist = exist_buf
m -= need_money
if m < 0:
ans -= 1
print(ans)
4. 飞机航线
5. n*3的网格求最高得分
有n*3的格子,每个格子都有一定的分数,最开始从第一行的任意一个格子进入,每一步只能向左下,正下,右下这三个方向走,遇到了分数为0的格子,之后所得的分数都要取相反数,分数可以多次反转,问,到达最后一行时,得到的最大分数是多少?
这题不会,看到牛客上的解法是 从后往前动态规划,初始状态是最后一行,用两个状态,一个最大,一个最小,如果遇到0就相互调换。
代码不会写
https://www.nowcoder.com/discuss/226306?type=post&order=time&pos=&page=1
https://www.nowcoder.com/discuss/226319?type=post&order=time&pos=&page=1
记录一下临时代码,这个是错的:
# ref https://www.nowcoder.com/discuss/226319?type=post&order=time&pos=&page=1
def func(nums, n): # nums数组是n行3列的
dp_max = [[0 for _ in range(3)] for _ in range(n)]
dp_min = [[0 for _ in range(3)] for _ in range(n)]
dp_max[-1] = nums[-1]
dp_min[-1] = nums[-1]
# print(dp_max)
for i in range(n - 1, -1, -1):
for j in range(3):
dp_max[i][j] = dp_max[i - 1][j]
dp_min[i][j] = dp_min[i - 1][j]
if j < 2:
dp_max[i][j] = max(dp_max[i][j], dp_max[i - 1][j + 1])
dp_min[i][j] = min(dp_min[i][j], dp_min[i - 1][j + 1])
if j < 0:
dp_max[i][j] = min(dp_max[i][j], dp_max[i - 1][i - 1])
dp_min[i][j] = min(dp_min[i][j], dp_min[i - 1][i - 1])
if nums[j] == 0:
dp_max[i][j], dp_min[i][j] = - dp_min[i][j], - dp_max[i][j]
else:
dp_max[i][j] += nums[i][j]
dp_min[i][j] += nums[i][j]
return dp_max, dp_min
nums = [[1, 2, 3],[8, 9, 10],[5, 0, 5],[-9, -8, -10], [0, 1, 2],[5, 4, 6]]
print(func(nums, 6))
小红书笔试题
有大神分享了AC解法 https://blog.csdn.net/qq_17550379/article/details/99708185
1. 字符串倒序(剑指offer59)
2. leetcode198 抢劫犯(重要)
那一题,不过多了一个要求,除了输出最大金额,还需要输出偷了多少家,如果有多种情况都能满足最大金额,则输出最少需要偷多少家。
我的思路(只AC了27%):动态规划,构造一个res数组,每个都是二维的,对于res[i][j],有两种情况,一种是不更新,则res[i][j] = res[i - 1],另一种是更新,res[i][j] = [res[i - 2][0] + nums[i], count], 这个count是不断累加的(后来发现不能用count这样加,应该是res[i - 2][1] + 1才对。
def func(nums):
if not nums:
return 0, 0
if len(nums) == 1:
return 1, 1
if len(nums) == 2:
return max(nums[0], nums[1]), 1
res = [[]] * len(nums)
res[0] = [nums[0],1]
res[1] = [max(nums[0], nums[1]), 1]
count = 1
for i in range(2, len(nums)):
if res[i - 1][0] >= res[i - 2][0] + nums[i]:
res[i] = res[i - 1]
else:
count += 1
res[i] = [res[i - 2][0] + nums[i], count]
if res[-1][0] != res[-2][0]:
return res[-1]
return res[-1] if res[-1][1] <= res[-1][1] else res[-2]
牛客上的AC解法一(基于我的思路修改):
def func(nums):
res = [[]] * len(nums)
res[0] = [nums[0],1]
res[1] = [max(nums[0], nums[1]), 1]
for i in range(2, len(nums)):
cur = res[i - 2][0] + nums[i]
count = res[i - 2][1] + 1
if cur > res[i - 1][0] or (cur == res[i - 1][0] and count < res[i - 1][1]): # 如果cur == res[i - 1][0],并且count大于res[i-1][1]的话,也没必要更新,只有count小于res[i-1][1]才需要更新。
res[i] = [cur, count] # 这个count是res[i - 2][1] + 1来的,不是直接累加
else:
res[i] = res[i - 1]
return res[-1]
代码可以优化下(也是一个AC代码): https://blog.csdn.net/qq_17550379/article/details/99708185
def func(nums):
pre, cur = [0,0],[0,0]
for i in range(len(nums)):
tmp, pre = pre[::], cur[::]
if tmp[0] + nums[i] > cur[0]:
cur[0] = tmp[0] + nums[i]
cur[1] = tmp[1] + 1
return cur[0], cur[1]
牛客上的AC解法二(维护两个dp数组):
def func(nums):
res = [0] * len(nums)
count = [1] * len(nums)
res[0] = nums[0]
res[1] = max(nums[0], nums[1])
for i in range(2, len(nums)):
res[i] = max(res[i - 1], res[i - 2] + nums[i])
if res[i] > res[i - 1]:
count[i] = count[i - 2] + 1
else:
count[i] = count[i - 1]
return res[-1], count[-1]
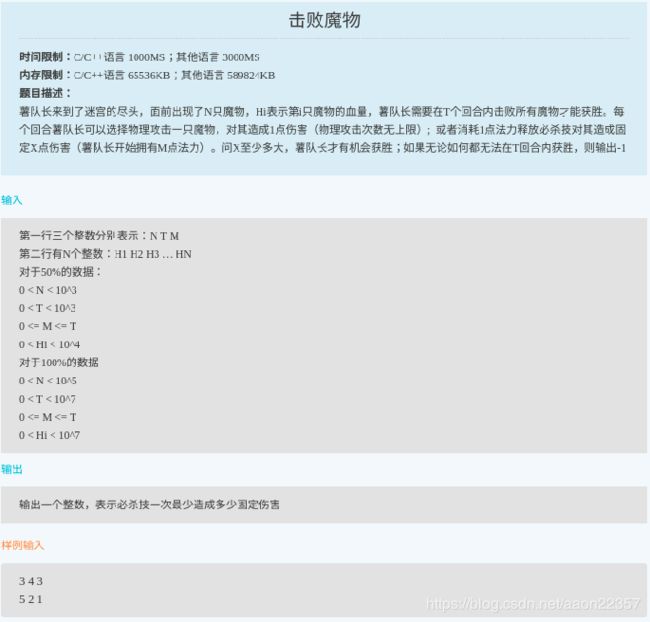
3.击败魔物(重要)
本题解法:贪心+二分。 H为怪物的血量数组,T为回合数,M为法力,X为每次施法造成的伤害,我们要求符合条件的最小的X。具体思路是:
-
第一步,判断特殊条件,如果
M + sum(H[M:]) > T,说明即使一次杀一个,也杀不完所有怪物(回合数T太小了),直接返回-1. -
对怪物的血量排一个降序(二分查找必须数组有序,贪心算法一般要求排降序)
-
使用二分法的思想,X的左边界
l =(sum(H) - (T - M)) // M,右边界r为最大的怪物血量r = H[0];然后求出mid = l + ((r - l) >> 1),判断X=mid时能否杀完,如果可以,将右边界缩为mid,如果不能,将左边界扩至mid + 1。关于左右边界初始值的思考:对于左边界有,M*X + (T - M) * 1 >= sum(H)),解出X的下界。
对于右边界有,如果X等于最大的怪物的血量,那么一次杀一个,肯定能杀完。
-
问题的关键就变成了:给定X = mid时,计算能否在T回合内杀完所有怪物,使用贪心的思想, 先遍历一遍数组,用每个怪物的血量整除X,计算能整除几次,累计一个值成为fali_need,然后将数组的每个元素都对X求余,得到余数的血量数组,并对这个数组继续降序排列(这个数组中的所有值都要比X小),此时的剩余法力为M - fali_need, 用这些剩余法力解决前M-fali_need个怪物(每个怪物血量都小于X,所以都可以一次解决),如果后面还有剩余的怪物,那么只能计算血量和sum,用物理攻击来解决,假设物理攻击使用了wuli_need次,那么最后统计M + wuli_need是否超过了回合数,如果没有超过,则返回True,证明当前的X是可以杀完怪物的。
分享牛客网上的AC代码: 【参考】
def list2gen(a):
for n in a:
yield n
def ismatch(X):
# 在达到目标时输出X
fali_need = 0
for Hi in list2gen(H):
fali_need += Hi // X
# fali_need = sum([Hi // X for Hi in H])
# 法力不够,用物理攻击弥补
if fali_need >= M:
wuli_need = X * (fali_need - M)
for Hi in list2gen(H):
wuli_need += Hi % X
# wuli_need += sum([Hi % X for Hi in H])
if M + wuli_need <= T: # M表示法力攻击轮数,wuli_need表示物理攻击轮数
return True
else:
return False
# 法力超出,多出来的这样用
# X=3,Hi=2,这样使用一次
else:
yushu = sorted([Hi % X for Hi in H])# 对余数降序排列(所有余数都比M要小,所以要用法力优先解决余数大的怪物)
wuli_need = sum(sorted(yushu)[::-1][M - fali_need :]) #剩余的法力为M-fali_need,用这些搞定前面的,后面剩余的全靠物理
if M + wuli_need <= T:
return True
else:
return False
def solution(N, T, M, H):
H = sorted(H)[::-1]
# 特殊情况
if M + sum(H[M:]) > T:
return -1
l = (sum(H) - (T - M)) // M
r = H[0]
# print(l, r)
while l < r:
mid = l + ((r - l) >> 1)
# print(f'mid: {mid}')
if ismatch(mid):
r = mid
else:
l = mid + 1
return l
import sys
line = sys.stdin.readline().strip()
N, T, M = list(map(int, line.split()))
line = sys.stdin.readline().strip()
H = list(map(int, line.split()))
print(solution(N, T, M, H))