论文阅读笔记:Fast R-CNN论文解读!
| Fast R-CNN论文解读! |
文章目录
- 一、Introduce
- 1.1、R-CNN and SPPnet
- 1.2、Contributions
- 二、Fast R-CNN architecture and training
- 2.1、Training
- 2.2、RoI pooling layer
- 2.3、Multi-task loss
- 2.4、Mini-batch sampling
- 2.5、Back-propagation through RoI pooling layers
- 2.6、SGD hyper-parameters
- 2.7、Scale invariance
- 三、 Fast R-CNN detection
- 3.1、 Truncated SVD for faster detection
- 参考博客
- 继2014年的RCNN之后,Ross Girshick在15年推出Fast RCNN,构思精巧,流程更为紧凑,大幅提升了目标检测的速度,Fast R-CNN论文下载链接。
一、Introduce
1.1、R-CNN and SPPnet
经典的R-CNN存在以下几个问题:
- 训练分多步骤:先在分类数据集上预训练,再进行fine-tune训练(R-CNN对整个CNN进行微调),然后再针对每个类别都训练一个线性SVM分类器,最后再用regressors对bounding box进行回归,并且bounding box还需要通过selective search生成。
- 时间和空间开销大:所有样本的特征需要存储到磁盘上(在训练SVM和回归的时候需要用网络训练的特征作为输入,特征保存在磁盘上再读入的时间开销较大)
- 检测速度慢:每张图片的每个region proposal都要做卷积,重复操作太多,这样一张图片大约需要2000次卷积。(R-CNN + VGG16:检测一张图需要47s)
在Fast RCNN之前提出过SPPnet来解决R-CNN中重复卷积问题,但SPPnet仍然存在与R-CNN类似的缺陷:
- 训练分多步骤: 需要SVM分类器,额外的regressors
- 空间开销大
RCNN很慢的原因主要是因为没有共享计算。SPP-net就通过共享计算提高了速度,它在ConvNet的最后一个卷积层才提取proposal,但是依然有不足之处。和R-CNN一样,它的训练要经过多个阶段,特征也要存在磁盘中,另外,SPP中的微调只更新spp层后面的全连接层,因为卷积特征是线下计算的,从而无法再微调阶段反向传播误差。对很深的网络这样肯定是不行的。
1.2、Contributions
Fast-RCNN的优点:
- 比R-CNN、SPP-net有更高的检测质量(mAP)
- 把多个任务的损失函数写到一起,实现单级的训练过程
- 在训练时可更新所有的层
- 不需要在磁盘中存储特征
二、Fast R-CNN architecture and training
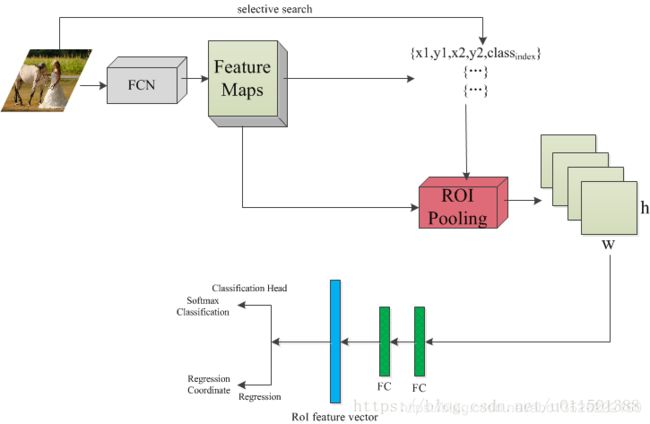
现在就按照下图的流程进行讲解。
- 首先是读入一张图像,这里有两个分支,一路送入FCN,输出 feature maps,另一路通过selective search提取region proposals(注意,Fast R-CNN论文中并没有明确说明使用selective search提取region proposals,但是Fast R-CNN是基于R-CNN的,姑且默认采用selective search提取region proposals吧。)提取的每个region proposal 都有一个对应的Ground-truth Bounding Box和Ground-truth class label
- 其中每个region proposals用四元数组进行定义,即 ( r , c , h , w ) (r, c, h, w) (r,c,h,w),即窗口的左上行列坐标与高和宽。值得注意的是,这里的坐标均是对应原图像的,而不是输出的feature maps
- 因此,还需要把原图像的坐标系映射到feature maps上。这一点也很简单,比如采用的是pre-trained 网络模型为VGG16的话,RoIPooling替换掉最后一个max pooling层的话,则原图像要经过4个max pooling层,输出的feature maps是原图像的1/16,因此,将原图像对应的四元数组转换到feature maps上就是每个值都除以16,并量化到最接近的整数。
- 那么将region proposal的四元组坐标映射到feature maps上之后接下干什么呢?接下来就是把region proposal窗口框起来的那部分feature maps输入到RoIPooling(R-CNN是将其缩放到224x224,然后送入经过Fine-tuning的网络模型),得到固定大小的输出maps。
2.1、Training
Fast R-CNN的网络结构如下图所示。
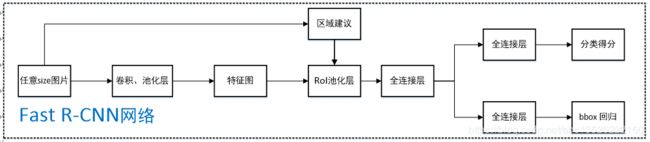
- 任意size图片输入CNN网络,经过若干卷积层与池化层,得到特征图;
- 在任意size图片上采用selective search算法提取约2k个建议框;
- 根据原图中建议框到特征图映射关系,在特征图中找到每个建议框对应的特征框【深度和特征图一致】,并在RoI池化层中将每个特征框池化到 H × W H×W H×W【VGG-16网络是 7 × 7 7×7 7×7】的size;
- 固定 H × W H×W H×W【VGG-16网络是7×7】大小的特征框经过全连接层得到固定大小的特征向量;
- 第4步所得特征向量经由各自的全连接层【由SVD分解实现】,分别得到两个输出向量:一个是softmax的分类得分,一个是Bounding-box窗口回归;
- 利用窗口得分分别对每一类物体进行非极大值抑制剔除重叠建议框,最终得到每个类别中回归修正后的得分最高的窗口。
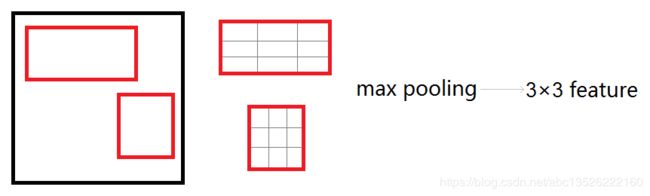
2.2、RoI pooling layer
ROIPooling层将每个候选区域均匀分成 H × W H×W H×W块,对每块进行max pooling。将特征图上大小不一的候选区域转变为大小统一的数据,送入下一层。 下图中是分成 3 × 3 3×3 3×3。
其思路如下:
- 将 region proposal 划分为 H × W H×W H×W大小的网格
- 对每一个网格做MaxPooling(即每一个网格对应一个输出值)
- 将所有输出值组合起来便形成固定大小为 H × W H×W H×W 的 feature map
注意: 对于ROIPooling不理解的,可以参考我之前博客中的3.2节,链接为:青年AI自强计划:第7章视觉探测任务R-CNN,Fast R-CNN,Faster R-CNN,YOLO!
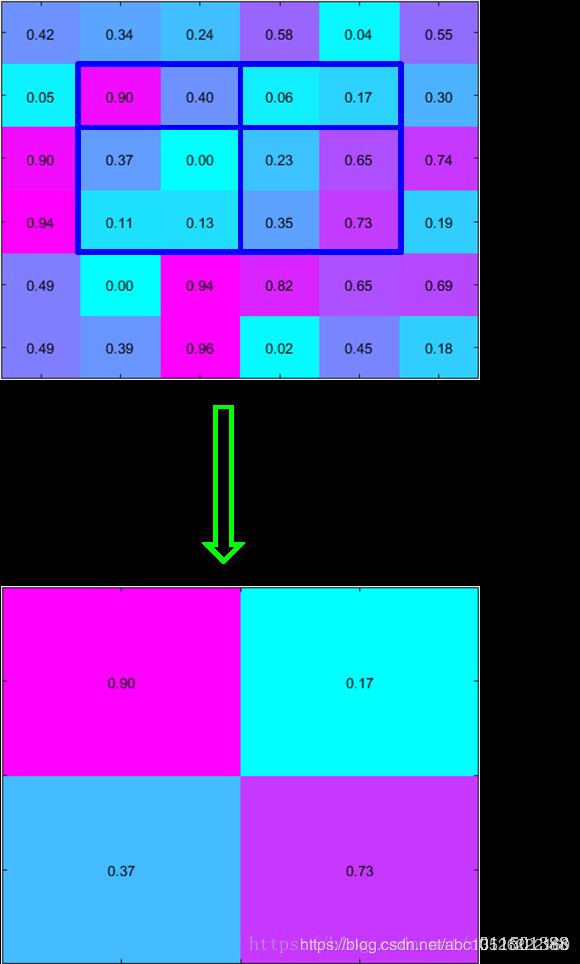
补充: 在图3中最外层蓝色的框即表示region proposal的四元组坐标映射到feature maps上,然后此框再经过划分网格,这里为2x2,所以最终的输出feature maps大小为2x2。值得注意的是,本应把region proposal的矩形框(window)均匀分成2x2的网格,但是feture map的坐标值均为整数值,不可避免存在一个就近取整的量化,导致有时无法实现均匀分割,(这个问题在Mask R-CNN中提出的RoIAlign层专门解决这个问题)。在Fast R-CNN论文中,在采用VGG16的时候,Conv5_x的输入feature map的spatial size是7x7的,所以在论文中把每个region proposal划分为7x7的网格,那么最终经过RoIPooling输出的feature maps的spatial size为7x7的。RoIPooling跟标准的 max pooling一样,是逐channel的。
2.3、Multi-task loss
多损失融合(分类损失和回归损失融合),分类采用log loss(即对真实分类的概率取负log,分类输出 K + 1 K+1 K+1维),回归的 loss 和 R-CNN基本一样。
Fast R-CNN网络分类损失和回归损失如下图所示【仅针对一个RoI即一类物体说明】,黄色框表示训练数据,绿色框表示输入目标:

- c l s cls cls_ s c o r e score score 层用于分类,输出 K + 1 K+1 K+1 维数组 p p p ,表示属于 K K K 类物体和背景的概率;
- b b o x bbox bbox_ p r e d i c t predict predict层用于调整候选区域位置,输出 4 × K 4×K 4×K 维数组,也就是说对于每个类别都会训练一个单独的回归器;
Fast RCNN有两个输出层:
- 一个对每个 R o I RoI RoI输出离散概率分布: p = ( p 0 , … , p K ) p=\left(p_{0}, \dots, p_{K}\right) p=(p0,…,pK)
- 一个输出bounding box回归的位移: t k = ( t x k , t y k , t w k , t h k ) , k ∈ K t^k=(t_x^k, t_y^k, t_w^k, t_h^k), k \in K tk=(txk,tyk,twk,thk),k∈K;k表示类别的索引,前两个参数是指相对于object proposal尺度不变的平移,后两个参数是指对数空间中相对于object proposal的高与宽。
每个训练的RoI都被标记了ground-truth类别 u u u 以及ground-truth边界框回归 v v v 。在每个标记好的RoI上用multi-task loss 函数来级联的训练分类和 b b o x bbox bbox 边界框回归:
(1) L ( p , u , t u , v ) = L c l s ( p , u ) + λ [ u ≥ 1 ] L l o c ( t u , v ) L\left(p, u, t^{u}, v\right)=L_{\mathrm{cls}}(p, u)+\lambda[u \geq 1] L_{\mathrm{loc}}\left(t^{u}, v\right)\tag{1} L(p,u,tu,v)=Lcls(p,u)+λ[u≥1]Lloc(tu,v)(1)
- 注意: 约定 u = 0 u=0 u=0为背景分类,那么 [ u ≥ 1 ] [u≥1] [u≥1] 函数表示背景候选区域即负样本不参与回归损失,不需要对候选区域进行回归操作;
- 第一项是对于 u u u 类的分类损失,log loss for true class u
(2) L c l s ( p , u ) = − log p u L_{\mathrm{cls}}(p, u)=-\log p_{u}\tag{2} Lcls(p,u)=−logpu(2) - 对于分类 l o s s loss loss,是一个 N + 1 N+1 N+1路的 s o f t m a x softmax softmax输出,其中的 N N N是类别个数,1是背景。
第二项是回归损失,是在 u u u 类的真正边界框回归目标的元组 v v v 上定义的,是一个 4 × N 4×N 4×N 路输出的regressor,也就是说对于每个类别都会训练一个单独的regressor,评估回归损失代价就是比较真实分类 u u u 对应的预测平移缩放参数和真实平移缩放参数的差距:
(3) L l o c ( t u , v ) = ∑ i ∈ { x , y , w , h } smooth L 1 ( t i u − v i ) L_{\mathrm{loc}}\left(t^{u}, v\right)=\sum_{i \in\{x, y, w, h\}} \operatorname{smooth}_{L_{1}}\left(t_{i}^{u}-v_{i}\right)\tag{3} Lloc(tu,v)=i∈{x,y,w,h}∑smoothL1(tiu−vi)(3)
其中: v = ( v x , v y , v w , v h ) v=\left(v_{\mathrm{x}}, v_{\mathrm{y}}, v_{\mathrm{w}}, v_{\mathrm{h}}\right) v=(vx,vy,vw,vh)是真实平移缩放参数;对于 u u u 重新预测 b b o x bbox bbox 回归平移缩放参数: t u = ( t x u , t y u , t w u , t h u ) t^{u}=\left(t_{\mathrm{x}}^{u}, t_{\mathrm{y}}^{u}, t_{\mathrm{w}}^{u}, t_{\mathrm{h}}^{u}\right) tu=(txu,tyu,twu,thu);这里的损失不是 L 2 L2 L2损失函数,而是 smooth L 1 ( x ) \operatorname{smooth}_{L_{1}}(x) smoothL1(x)损失函数,对于离群点不敏感,因为有 L 2 L2 L2损失的训练可能需要仔细调整学习率,以防止爆炸梯度(控制梯度的量级使得训练时不容易跑飞)。公式如下:
(4) smooth L 1 ( x ) = { 0.5 x 2 if ∣ x ∣ < 1 ∣ x ∣ − 0.5 otherwise \operatorname{smooth}_{L_{1}}(x)=\left\{\begin{array}{ll}{0.5 x^{2}} & {\text { if }|x|<1} \\ {|x|-0.5} & {\text { otherwise }}\end{array}\right.\tag{4} smoothL1(x)={0.5x2∣x∣−0.5 if ∣x∣<1 otherwise (4) - 超参数 λ λ λ 是用来控制两个损失函数的平衡的。作者对回归目标进行归一化使其具有零均值及单位权方差(zero mean and unit variance)。所有的函数都设置超参数 λ = 1 λ = 1 λ=1。
下图我用 p y t h o n python python,把 smooth L 1 ( x ) \operatorname{smooth}_{L_{1}}(x) smoothL1(x)用蓝色部分表示出来了。现在这样有一个好处:如果 ∣ x ∣ > 1 |x|>1 ∣x∣>1,本来的 0.5 x 2 0.5 x^{2} 0.5x2二次项函数变为了一次项 ∣ x ∣ − 0.5 |x|-0.5 ∣x∣−0.5(梯度变小了很多),对也偏离过大的可以防止梯度一下变化太大,更好的鲁棒性,原本的虚线部分 L 2 L2 L2 l o s s loss loss二次损失函数,可以看出来偏离大的时候,梯度非常的大,容易梯度爆炸。

2.4、Mini-batch sampling
作者从对象建议框(object proposal)中选择25%的RoI,这些RoI与ground-truth bbox边界框至少有0.5的部分交叉重叠,也就是正样本,即 u > = 1 u >= 1 u>=1。其余的RoI选那些IoU重叠区间在[0.1,0.5)的,作为负样本,即 u = 0 u = 0 u=0,大约为75%。之所以选择负样本需要大于0.1的阈值是因为使用启发式的hard example mining(低于0.1的IoU作为难例挖掘的启发式)。在训练期间,图像有0.5的概率水平翻转。
| 类别 | 比例 | 方式 |
|---|---|---|
| 前景 | 25% | 与ground-truth bbox边界框重叠区间在 [ 0.5 , 1 ] [0.5,1] [0.5,1] |
| 背景 | 75% | 与ground-truth bbox边界框重叠区间在 [ 0.1 , 0.5 ) [0.1,0.5) [0.1,0.5) |
2.5、Back-propagation through RoI pooling layers
说实话,池化层的反向传播这里我也并没有看懂,通过RoI池化层的反向传播。首先看普通max pooling层如何求导,设 x i x_{i} xi 为输入层节点, y i y_{i} yi 为输出层节点,那么损失函数 L L L 对输入层节点 x i x_{i} xi 的梯度为:
(5) ∂ L ∂ x i = { 0 , δ ( i , j ) = false ∂ L ∂ y j , δ ( i , j ) = true \frac{\partial L}{\partial x_{i}}=\left\{\begin{array}{ll}{0,} & {\delta(i, j)=\text { false }} \\ {\frac{\partial L}{\partial y_{j}},} & {\delta(i, j)=\text { true }}\end{array}\right.\tag{5} ∂xi∂L={0,∂yj∂L,δ(i,j)= false δ(i,j)= true (5)
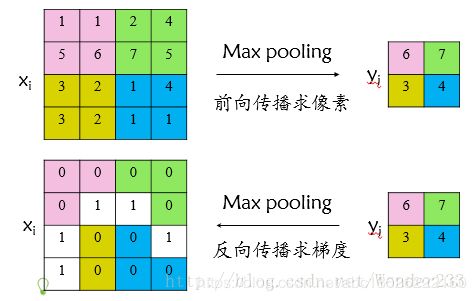
其中判决函数 δ ( i , j ) δ(i,j) δ(i,j)表示输入 i i i 节点是否被输出 j j j节点选为最大值输出。
不被选中【 δ ( i , j ) = f a l s e δ(i,j)=false δ(i,j)=false】有两种可能: x i x_{i} xi不在 y i y_{i} yi 范围内,或者 x i x_{i} xi 不是最大值。
若选中【 δ ( i , j ) = t r u e δ(i,j)=true δ(i,j)=true 】则由链式规则可知损失函数 L L L相对 x i x_{i} xi 的梯度等于损失函数 L L L相对 y i y_{i} yi 的梯度 × × ×( y i y_{i} yi对 x i x_{i} xi的梯度->恒等于1),故可得上述所示公式;
具体如何求导可以参考作者:RCNN学习笔记(2):Fast R-CNN
2.6、SGD hyper-parameters
SGD超参数选择:
- 除了修改增加的层,原有的层参数已经通过预训练方式初始化:
- 用于分类的全连接层以均值为0、标准差为0.01的高斯分布初始化;
- 用于回归的全连接层以均值为0、标准差为0.001的高斯分布初始化,偏置都初始化为0;
针对PASCAL VOC 2007和2012训练集:
- 前30k次迭代全局学习率为0.001,每层权重学习率为1倍,偏置学习率为2倍,后10k次迭代全局学习率更新为0.0001;
- 动量设置为0.9,权重衰减设置为0.0005。
2.7、Scale invariance
尺度不变性,作者提出了使用两种方式对规模不变的对象进行检测:brute-force(单一尺度)和image pyramids(多尺度,图像金字塔)。
- 单一尺度直接在训练和测试阶段将image预先固定好像素大小,直接输入网络训练就好,然后期望在训练过程中网络自己能够学习到尺度不变性scale-invariance;
- 多尺度在训练阶段随机从图像金字塔【缩放图片的scale得到,得到多尺度图片,相当于扩充数据集】 中采样训练,通过一个图像金字塔向网络提供一个近似的尺度不变,在测试阶段图像金字塔用来对每个object proposal近似尺度归一化,训练阶段每次采样一个图像就随机采样一个金字塔尺度。
作者在5.2节对单一尺度和多尺度分别进行了实验,不管哪种方式下都定义图像短边像素为s,
-
单一尺度下s=600【维持长宽比进行缩放】,长边限制为1000像素;
-
多尺度 S = { 480 , 576 , 688 , 864 , 1200 } S=\{480,576,688,864,1200\} S={480,576,688,864,1200}【维持长宽比进行缩放】,长边限制为2000像素,生成图像金字塔进行训练测试;
-
实验结果表明AlexNet【S for small】、VGG_CNN_M_1024【M for medium】下单一尺度比多尺度mAP差1.2%~1.5%,但测试时间上却快不少,VGG-16【L for large】下仅单一尺度就达到了66.9%的mAP【由于GPU显存限制多尺度无法实现】。该实验证明了深度神经网络善于直接学习尺度不变形,对目标的scale不敏感。
-
第2中方法的表现确实比1好,但是好的不算太多,大概是1个mAP左右,但是时间要慢不少,所以作者实际采用的是第一个策略,也就是single scale。
三、 Fast R-CNN detection
一旦Fast R-CNN网络被微调,检测相当于运行正向传播(假设对象建议框object proposal是预先计算的)。
- 网络将图像(或图像金字塔,编码为图像列表)和待给得分的 R 对象建议框(object proposal)列表作为输入。
- 在测试阶段,Rol 大约为2K个,当使用图像金字塔的时候,每个RoI被指定尺度使得接近224*224。对于每个测试RoI r ,网络输出关于 r 的一个后验概率分布 p 和一系列预测bbox偏移(每个类 [共k个类] 获得自己的精确bbox预测)。然后使用估计概率 Pr ( class = k ∣ r ) ≜ p k \operatorname{Pr}(\text { class }=k | r) \triangleq p_{k} Pr( class =k∣r)≜pk给 r 赋予关于 k 个对象类的检测置信度。最后给每个类都实施一个非极大值抑制。
3.1、 Truncated SVD for faster detection
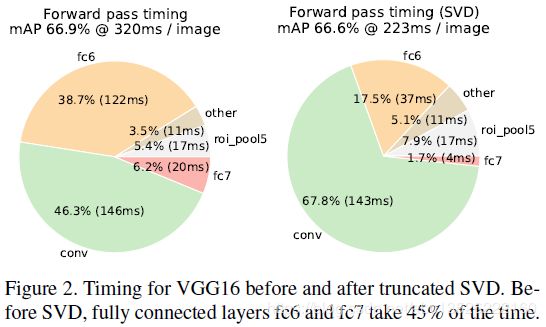
截断式的奇异值分解(SVD)只需要少量的奇异值分解,就可以将检测时间缩短30%以上;这是论文第二个改进点,第一个是改进loss。
- 图像分类任务中,用于卷积层计算的时间比用于全连接层计算的时间多;
- 而在目标检测任务中,要处理的RoI数量比较多,几乎有一半的前向计算时间被用于全连接层(Figure 2)。就Fast R-CNN而言,RoI池化层后的全连接层需要进行约2k次【每个RoI都要计算】,因此在Fast R-CNN中可以采用SVD分解加速全连接层计算;
具体如何实现的呢?
- 物体分类和bbox回归都是通过全连接层实现的,假设全连接层输入数据为 x x x,输出数据为 y y y,全连接层权值矩阵为 W W W,尺寸为 u × v u × v u×v ,那么该层全连接计算为:
(6) y = W × x y=W \times x\tag{6} y=W×x(6)
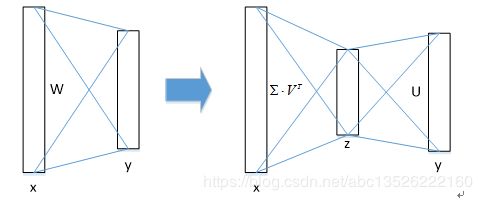
计算复杂度为 u × v u×v u×v; - 若将 W W W 进行SVD分解(奇异值分解),并用前 t t t 个特征值近似代替,即:
(7) W = U ∑ V T ≈ U ( u , 1 : t ) ⋅ ∑ ( 1 : t , 1 : t ) ⋅ V ( v , 1 : t ) T W=U\sum V^T\approx U(u,1:t)\cdot \sum(1:t,1:t)\cdot V(v,1:t)^T\tag{7} W=U∑VT≈U(u,1:t)⋅∑(1:t,1:t)⋅V(v,1:t)T(7)
U U U是 u × t u × t u×t 的左奇异矩阵, ∑ \sum ∑是 t × t t × t t×t 的对角矩阵 , V V V是 v × t v × t v×t 的右奇异矩阵。
那么原来的前向传播分解成两步:
(8) y = W x = U ⋅ ( ∑ ⋅ V T ) ⋅ x = U ⋅ z y=Wx=U\cdot(\sum\cdot V^T)\cdot x=U\cdot z\tag{8} y=Wx=U⋅(∑⋅VT)⋅x=U⋅z(8)
计算复杂度为 u × t + v × t u×t+v×t u×t+v×t,若 t < m i n ( u , v ) t<min(u,v) t<min(u,v),则这种分解会大大减少计算量; - 在实现时,相当于把一个全连接层拆分为两个全连接层,第一个全连接层不含偏置,第二个全连接层含偏置;实验表明,SVD分解全连接层能使mAP只下降0.3%的情况下提升30%的速度,同时该方法也不必再执行额外的微调操作。
补充: 这里要是不理解奇异值分解(SVD),可以参考我之前的博客,里面有详细介绍:奇异值分解SVD(Singular Value Decomposition)总结
参考博客
主要参考了下面作者的文章,虽然有些细节还没有完全搞懂,在这里表示感谢!
- Fast R-CNN论文详解,主要参考了这个,作者写的特别好!
- 【目标检测】Fast RCNN算法详解
- 目标检测之 Fast R-CNN
- Fast RCNN算法详解