计算理论重点——Theory of Computation

一个学期的计算理论课程已经结束，给我的感觉吧，计算理论是一门计算机不得不学，学了短期又没用，但是可以培养一些逻辑思维的课程。其最关注的问题是什么是可计算性，什么问题可计算，问题之间的映射/归约，计算代价及难易。在分析问题和检验模型计算能力之前需要掌握的工具是形式语言、图灵机等。本文主要对计算理论中的重点进行了总结，总结了一些定理和理解上容易有障碍的知识点，但是里面还有一些点没有提到，比如NFA、DFA的相互转化，CFL和PDA的相互转化，需要书中的题目和证明辅助。

 

Textbook Summary

1.       与自然数集合N等势的集合是可数无穷的，称有穷的or可数无穷的集合是可数的。非可数的集合称作不可数的。

2.       DFA( K, Σ, s, F, δ )；NFA（K,Σ，s，F，Δ）

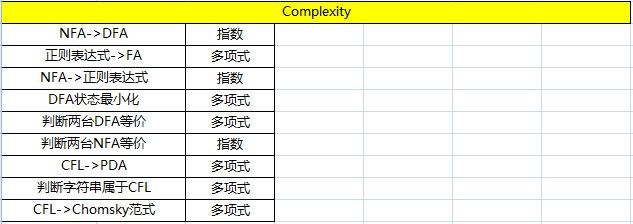
3.       每台NFA都有一台等价的DFA（method:find closure）

4.       有穷自动机接受的语言类= 正则语言类（正则表达式描述的语言类）

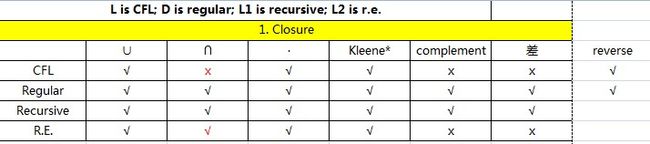
5.       正则语言在各种运算下封闭

6.       语言是正则的，iff其等价语言中有有穷个等价类。

7.       DFA状态最小化->寻找等价类（初始等价类F& K-F）

8.       CFL（V，Σ，R，S）

9.       存在非正则的CFL

10.   能够生成>=两棵语法分析树的字符串的文法叫做歧义的。

11.   PDAM=（K，Σ，Γ，Δ，s，F），Γ为栈符号

12.   PDA接受的语言正好是CFL

13.   正则语言（xyⁿz）和CFL（uvⁿxyⁿz）的泵定理

14.   L={aⁿbⁿ}∈CFL，L={aⁿbⁿcⁿ}∉CFL但是是递归的，L={aⁿ,n为素数}不是CFL

15.   Chomsky范式（CNF）：若RÍ(V-Σ)×V²，则称G=（V，Σ，R，S）为Chomsky范式

16.   有穷自动机总是停机。

17.   CFG到CNF的转化：

1)      消除长rules

2)      消除空rules（A->e）

3)      消除短rules（A->aor A->B）

18.   对任意CFLG，都可以在多项式时间构造Chomsky范式G’,使得L(G’)=L(G)-(Σ∪{e})

19.   没有chomsky范式能够表示length<2的字符串，所以包含<2的字符串的语言不能转化到chomsky范式。

20.   确定型CFL（确定型PDA接受的语言类）在补下封闭。

21.   TM(K，Σ，δ，s，H)，注意字母表Σ不包含←和→

22.   若存在TM判定L，则称L是递归的。

23.   如果对于所有w属于Σ*，M(w) = f(w)，我们说M计算函数f，若存在TM计算f，则f称为递归的。

24.   半判定语言的TM都不是算法

25.   多带、多带头、双向无穷带or多维带的TM，其判定or半判定的任何语言及任何函数，都分别可用标准TM判定、半判定or计算。

26.   非确定型TM：一个格局可在一步里产生多个其他格局，NDTM is no more powerful than original TM

27.   若非确定型TMM半判定或者判定语言L，或者计算函数f，则存在标准型TMM’半判定or判定L，or计算函数f。

28.   文法是CFG的推广，任何CFG都是文法。G=（V，Σ，R，S）

29.   语言被文法生成iff它是r.e.的。

30.   所有数值函数都是原始递归的

31.   原始递归函数集是递归可枚举的。

32.   特殊语言/问题：

H = {“M””w”: M在w上停机 }

﹁H = { “M””w”：M是一台在”w”上不停机的TM}

H1 = {“M”：M在“M”上停机 }

﹁H1 = { w：要么w不是一台TM的编码，

要么w是M的编码，M是一台在”M”上不停机的TM}

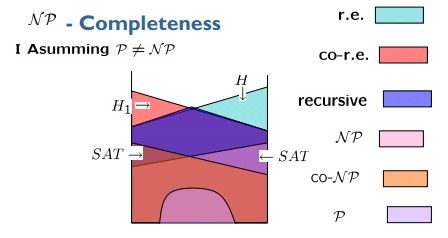
H：r.e. ;    H1：r.e.；  ﹁H, ﹁H1：非r.e.；2-SAT∈P；   SAT∈NP

33.   没有算法的问题称作不可判定的or不可解的，如TM的停机问题

34.   证明不可判定：从通用图灵机U通过递归函数归约到L，如果L是递归的则U是递归的。

i.e.若L1非递归，并存在L1到L2的归约，则L2也非递归。

递归函数是TuringComputable的。

35.   语言是图灵可枚举的，iff存在枚举它的图灵机。（M通过空格代开始，周期性的经过特殊状态q来枚举L，任意顺序且可重复）

36.   不可判定语言与递归语言互为补集，与r.e.语言有交集。

37.   语言是r.e.，iff它是图灵可枚举的；语言是递归的，iff它是以字典序Turing可枚举的。

38.   P在并交连接和补运算下封闭，NP在并、连接运算下封闭。若NP在补下封闭，则NP=P。

39.   H= {“M””w”: M在最多2^|w|步后停机 } ∉P

40.   所有正则语言和所有CFL都属于P

41.   NP：

A.      机器角度去定义：被多项式界限非确定型图灵机判定的所有语言的类。

B.      基于verifier的定义：NP问题上建立的非确定机包含两步：

1)           非确定地猜一个解

2)           用一个确定的算法判定该解是否为可行解

判定一个给定猜测值是否满足该问题（可满足性）的算法称作verifier，一个问题称作NP问题当且仅当存在一个多项式时间的verifier。

这两个定义是不矛盾的，因为如果一台非确定TM在多项式时间内可以判定一个非确定选择的输入是否满足，就是基于verifier的定义。

P和NP的区别：

A problem isin P if we can decide them in polynomial time. It is in NP if we can decidethem in polynomial time, if we are given the rightcertificate.

42.   若存在计算函数f的多项式界限的图灵机M，则f称为多项式时间可计算的。

43.   若τ1是L1->L2的多项式归约，τ2是L2->L3的多项式归约，则τ1·τ2是L1->L3的多项式归约。

44.   证明NP完全：

法一、按定义：LÍΣ*，若

（a）      L∈NP，且

（b）     对每个语言L’∈NP，存在从L’到L的多项式归约

则L称为NP完全的。

法二、归约，对于语言L，

（a）      若L∈NP

（b）     一个NP完全问题可以在多项式时间规约到L，i.e.SAT ≤_pL

则L称为NP完全的。

45.   L是NP完全语言，则P=NP，iffL∈P

46.   SAT是NP-complete，3-SAT，最大可满足性也是NP完全的

47.   覆盖问题，Hamilton圈（有向无向），旅行商问题，背包问题都是NP-complete。

48.   a*b*c*- {aⁿbⁿcⁿ, n ≥0} is context-free but not regular

49.   L=L1L2，L是CFL，则L1一定是CFL（×）

50.   Regular-CFL不一定是CFL，如a*b*c*-anbn包含anbncn

51.   2-wayPDA(i.e. PDA whose input heads can move both left and right) are more powerfulthan 1-way PDA

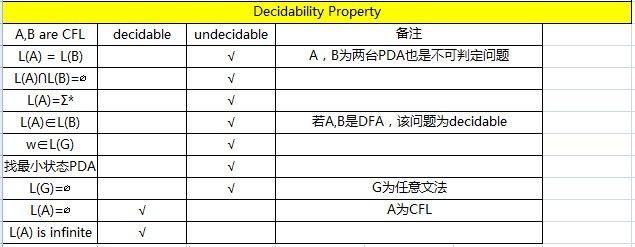
52.   Givena PDA M1 and an FA M2, the problem L(M1) ÍL(M2)is decidable

53.   DFA/NFA识别的是exactly正则语言。

54.   R.e.只在补和差下不封闭，CFL在交下也不封闭。

55.   非正则语言的*可能是正则语言。比如A:{w=w^R },及所有回文，A*=Σ*，为正则语言

56.   典型非正则：w=w^R

57.   正则语言的子集可能非正则，如aⁿbⁿcⁿ,是a*b*c*的子集；又如Σ*是正则语言，H⊆Σ*。

58.   归约：X到Y的归约可以理解为X到Y问题的映射,reduction可以解释为at least as difficult as… 比如X可以被Y的算法解决，则Xis no more difficult than Y, X可以归约到Y，记X≤Y。e.g. x²可以归约到任意两数的乘积。

∴ 若有A≤_rB，

A是不可判定问题->B不可判定    A不递归->B不递归

B可判定->A可判定              B是递归的->A是递归的

59.   若X多项式时间归约到Y，Y多项式时间可解，则X多项式时间可解；

若X多项式时间归约到Y，X多项式时间不可解，则Y多项式时间不可解

60.   X多项式时间归约到Y，Y多项式时间归约到Z，则X多项式时间归约到Z

61.   PRIME（COMPOSITE）多项式时间归约到Factor，但是Factor多项式时间不能归约到PRIME（COMPOSITE）。

62.   若A≤_PB，B∈NP，则A∈NP。

证明：

A≤_PBÞ存在确定图灵机X，可将A归约到B。

B∈NPÞ 存在一个非确定图灵机N可判定B。

我们希望构造一个新的TM（X*N），是的X*N非确定多项式时间求解A，则A∈NP。

Running time of X*N≤1+p(n)B>+q(p(n))(B多项式时间非确定判定)是多项式时间

所以A∈NP

63.   若A≤_PB，B∈P，则A∈P。

64.   若X是NPC的，则X在多项式时间内可解iffP=NP.

65.   SAT多项式时间归约到3-SAT(3-SAT是NPC的)

66.   证明语言L是R./R.e./NonR.e.

a)        Intuitively想想有没有半判定（判定）的TM，有则R.e.(R)。若非R,执行下一步。

b)       用能否由R.e.（Non R.e.）语言归约到该语言，能则R.e.而非R（NonR.e）.

严格用归约函数定义f：A≤_pB，r1∈A当且仅当f(r1)∈B

e.g.1  ∈H, iff M∈L 证明R.e.

e.g.2  ∈非H，iffM∈L 证明Non R.e.

注意方向：是从A的实例经过递归函数推向B的实例。

详细介绍：http://www.cs.rice.edu/~nakhleh/COMP481/final_review_sp06_sol.pdf

67.   递归与μ递归等价

68.   PDA中，若每一个格局至多有一个格局接在它后面，则为确定型的。确定型CFL在补下封闭。

69.   M半判定L：w∈L，iff M在w上停机，注意半判定图灵机中不存在“拒绝”状态。只要不接受w，就不停机。

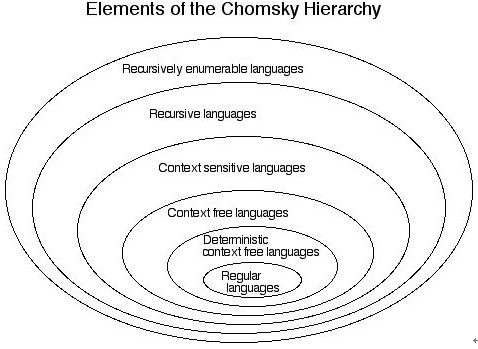
70.   Chomsky hierarchy

71.   俩证明：

7.6 证明P在并、交、Kleene*连接和补运算下封闭。

(1) 并：

对任意 L₁, L₂ÎP，设有n^a时间图灵机M₁和n^b时间图灵机M₂ 判定它们，且c=max{a,b}。

对L₁ÈL₂构造判定器M:

M=“对于输入字符串w :

1)     在w上运行M₁，在w上运行M₂。

2)     若有一个接受则接受，否则拒绝。”

 时间复杂度：设M₁为O(n^a),M₂为O(n^b)。令c=max{a,b}。

     第一步用时O(n^a+n^b) ，因此总时间为O(n^a+ n^b)=O(n^c),

 所以L₁ÈL₂属于P类，即 P在并的运算下封闭。

 

(2) 连接：

对任意 L₁, L₂属于P 类，设有n^a时间图灵机M₁和n^b时间图灵机M₂ 判定它们，且c=max{a,b}。对L₁L₂ 构造判定器M:

M=“对于输入字符串w=w₁,w₂,…,w_n，

1)     对k=0,1,2,…,n重复下列步骤。

2)          在w₁w₂…w_k上运行M₁，在w_k+1w_k+2…w_n上运行M₂。

3)          若都接受，则接受。否则继续。

4)     若对所有分法都不接受则拒绝。“

    时间复杂度：(n+1)×(O(n^a)+O(n^b))=O(n^a+1)+O(n^b+1)=O(n^c+1)，所以L₁L₂属于P类，即 P在连接的运算下封闭。

 

(3)补：

对任意 L₁属于P 类，设有时间O(n^a)判定器M₁判定它，对构造判定器M:

M=“对于输入字符串w :

(1)  在w上运行M₁。

(2)  若M₁接受则拒绝，若M₁拒绝则接受。”

时间复杂度为：O(n^a)。所以属于P类，即 P在补的运算下封闭 。

 

7.7 证明NP在并和连接运算下封闭。

(1) 并：

对任意 L₁, L₂ÎNP，设分别有n^a时间非确定图灵机M₁和n^b时间非确定图灵机M₂ 判定它们，且c=max{a,b}。

构造判定L₁ÈL₂的非确定图灵机M:

M=“对于输入字符串w :

1)     在w上运行M₁，在w上运行M₂。

2)     若有一个接受则接受，否则拒绝。”

对于每一个非确定计算分支，第一步用时为O(n^a)+O(n^b)，因此总时间为O(n^a+n^b)=O(n^c)。 所以L₁ÈL₂ÎNP，即 NP在并的运算下封闭。

(2) 连接：

对任意 L₁, L₂ÎNP，设分别有n^a时间非确定图灵机M₁和n^b时间非确定图灵机M₂ 判定它们，且c=max{a,b}。

构造判定L₁L₂的非确定图灵机M:

M=“对于输入字符串w :

1)     非确定地将分成两段x,y，使得w=xy。

2)     在x上运行M₁，在y上运行M₂。

3)     若都接受则接受，否则拒绝。”

对于每一个非确定计算分支，第一步用时O(n),第二步用时为O(n^a)+O(n^b)，因此总时间为O(n^a+ n^b)=O(n^c)。 所以L₁L₂ÎNP，即NP在连接运算下封闭。

 

 

 

 

 

 

专题——图灵机可判定性问题

判定以下问题是否可判定：
声明：思路——想证明B问题不可解，
1.       从一个不可解问题A入手（如停机问题）
2.       创建B的一个实例，从中推出如果能解决B，A也就可以解决了

3.       所以B是不可解的

1.       一个图灵机有至少481个状态。
我们可以给出这样一个TMN进行enc（M），
a)       数M中状态数，直到481.

b)       如果达到了481，N就接受，否则拒绝。

2.       给定图灵机在空串上走了481步还没停机。
构造2带图灵机N，
a)       2nd 带: 写481个0
b)       1st 带在空串上模拟M，每走一步，第2带就删掉一个0

c)        如果M在所有0都删掉之后停机，则N接受，否则不接受

3.       给定图灵机，判定它是否在一些输入上经过481步还没停机？
a)       按字典序找出所有length<=481的串x
b)       在每个x上面run M，看是否在481步以内停机

c)        是则接受，否则reject

4.       给定图灵机，判定在所有输入上是否经过481步还没停机？

a)       原因同(3)类似

5.       给定图灵机是否接受空串？
设两个语言：L1= {M|M(e)停机}；H = {|M(w)停机}

已知H不可判定，只需要找到H->L1的归约即可。令f(“M”,“w”) =M’(y) = “M(w)”, M’ 输入任何y的输出都是M在w上的模拟结果（获得的具体做法是删除任何输入，写入w，再在w上模拟M）。则{“M”,”w“}∈H，iffM’ 在任何串上停机，iff M’在空串停机 M‘∈L1。

6.       ①给定TM M，是否存在在M上停机的串？
②给定TM M， M是否在所有上停机的串？
设L = {M|M(a) where a∈Σ*} ，H = {|M(w)停机}。寻找H到L的归约。

令f(“M”,“w”) =M’(y) = “M(w)”, M’ 输入任何y输出都是M在w上的模拟结果（获得的具体做法是删除任何输入，写入w，再在w上模拟M）。{“M”,”w“}∈H，iffM’ 在任何串上停机，iff M’在任何串上停机，iff M’在所有a上停机(a∈Σ*), i.e. M’∈L。

7.       给定TM M，is L(M) finite?
设Finite = {L(M) where L(M) isfinite}; AH = {|M accept w}

存在从AH（非递归）到﹁Finite的递归函数f，f(“M”,“w”)=M’(y) = “M(w)”, 显然f可计算。则{M,w}∈AH iff M halts on w iff M’ accept any y∈Σ*ifff(M,w) is infinite, i.e. M’∈ ﹁Finite。由于AH归约到﹁Finite，所以﹁Finite非确定，又∵确定性在补下封闭，所以Finite也是非确定的。

8.       给定TM M, 带上是否出现过a（a∈Σ）？
设Write_a = {|M有一条在带上写a的规则}；AH = {|M accept w}
存在从AH（非递归）到﹁Finite的递归函数f，f(“M”,“w”)=M’(“T”,”a”) = Simulate M(w).
若M接受w，在带上写a；否则什么也不写。

则{M,w}∈AH iffM halts on w iffM’在带上写了一个aiff f(“M”,“w”)∈Write_a. 所以Write_a非确定。

9.       给定M1，M2，它们是否在一个相同串上停机？
设2Halts = {|存在令他们都停机的串w}；H = {|M(w)停机}

构造新机器M’，在M’带上写w，模拟M1若停机则清空带，写w，再模拟M2，若M2在w上也停机，则M’停机。则有M’停机iff∈2Halt iff∈H且∈H。

10.   给定M，只要M接受w，M就接受wR  
设S = {M| M accepts wRwhenever it accept w}; AH = {|M acceptw}
递归函数f定义如下，f(M,w)= M’(y), 在M’上模拟M(w).
当M接受w时，create M’ 只接受串1111；当M拒绝w时，create M’只接受串01。
则∈AH iff M接受w iff M’只接受1111 iffM’∈S，类似的∉AHiffM’接受01不接受10iffM’∉S
 




判定语言Recursive/Recursive Enumerable / Not R.e.
1.        L1 = {M| there exists an input on which M haltsin less than || steps}  R.
Test on all w less than |M|
2.        L2 = {M| |L(M)|<4} Not R.e.
a)      Reductionfrom H , 说明是R.e.或非R.e.
b)      ∈非H，当且仅当M’属于L2
3.        L3 = {M| |L(M)|>2} R.e. not R
 

由于本文有一些符号blog上无法显示，整理成PDF放在这里了，免费，欢迎下载。

本文整理于2013.01.10，最后更新2013.01.17，整理人Rachel_Zhang,感谢金小刚老师授课。