感知机的 python 实现
本文的主要内容是感知机的python实现。在阅读程序之前,如果对感知机的原理不了解,可以参考我的上一篇文章:感知机算法原理(PLA原理)及 Python 实现
创建一些用于测试的线性可分数据
机器学习是数据驱动的学科,如果您在网络上很难找到线性可分的数据的话,不妨自己来“捏造一些”。顺便提一下,因为我没有给我的 ubuntu 上的 sublime 添加中文支持,无法输入中文,所以注释使用英文写的。我会在代码中解释。
首先,新建一个名为 pla.py 的文件,将下面的代码添加进去,以导入 numpy 科学计算模块。
from numpy import *然后,我们来定义一个函数makeLinearSeparableData以产生我们需要的线性可分的数据。将下面的代码添加到 pla.py 中:
def makeLinearSeparableData(weights, numLines):
''' (list, int) -> array
Return a linear Separable data set.
Randomly generate numLines points on both sides of
the hyperplane weights * x = 0.
Notice: weights and x are vectors.
>>> data = pla.makeLinearSeparableData([2,3],5)
>>> data
array([[ 0.54686091, 3.60017244, 1. ],
[ 2.0201362 , 7.5046425 , 1. ],
[-3.14522458, -7.19333582, -1. ],
[ 9.72172678, -7.99611918, -1. ],
[ 9.68903615, 2.10184495, 1. ]])
>>> data = pla.makeLinearSeparableData([4,3,2],10)
>>> data
array([[ -4.74893955e+00, -5.38593555e+00, 1.22988454e+00, -1.00000000e+00],
[ 4.13768071e-01, -2.64984892e+00, -5.45073234e-03, -1.00000000e+00],
[ -2.17918583e+00, -6.48560310e+00, -3.96546373e+00, -1.00000000e+00],
[ -4.34244286e+00, 4.24327022e+00, -5.32551053e+00, -1.00000000e+00],
[ -2.55826469e+00, 2.65490732e+00, -6.38022703e+00, -1.00000000e+00],
[ -9.08136968e+00, 2.68875119e+00, -9.09804786e+00, -1.00000000e+00],
[ -3.80332893e+00, 7.21070373e+00, -8.70106682e+00, -1.00000000e+00],
[ -6.49790176e+00, -2.34409845e+00, 4.69422613e+00, -1.00000000e+00],
[ -2.57471371e+00, -4.64746879e+00, -2.44909463e+00, -1.00000000e+00],
[ -5.80930468e+00, -9.34624147e+00, 6.54159660e+00, -1.00000000e+00]])
'''
w = array(weights)
numFeatures = len(weights)
dataSet = zeros((numLines, numFeatures + 1))
for i in range(numLines):
x = random.rand(1, numFeatures) * 20 - 10
innerProduct = sum(w * x)
if innerProduct <= 0:
dataSet[i] = append(x, -1)
else:
dataSet[i] = append(x, 1)
return dataSet代码解释如下:
weights是一个列表,里面存储的是我们用来产生随机数据的那条直线的法向量。numLines是一个正整数,表示需要创建多少个数据点。numFeatures是一个正整数,代表特征的数量dataSet = zeros((numLines, numFeatures + 1))用于创建一个规模为numLines x (numFeatures + 1)的数组,且内容全为 0。注意:numFeatures + 1是为了在最后一列可以存储该数据点的分类(+1或者-1)。- 然后我们在
for循环里面填充dataSet的每一行。 x = random.rand(1, numFeatures) * 20 - 10产生一个数组,规模为一行,numFeatures列, 每个数都是 -10 到 10 的随机数。innerProduct = sum(w * x)计算内积- 接下来的
if语句判断如果内积小于等于 0,则是负例,否则是正例 numpy提供的append函数可以扩充一维数组,可以自己实验一下。- 最后返回数据集合。
函数的 docstring里面提供了使用例子,可以自己试一下,因为是随机数,所以结果不会相同。
我们可以实验一下。在Linux中,首先在pla.py所在目录打开 python 命令提示符,输入如下图所示命令:
Windows中只需直接运行我们编写的模块调,然后用函数
makeLinearSeparableData 即可。
将数据集可视化
得到了随机产生的数据集,当然要画画图看看是不是真的是线性可分的。下面是绘制散点图的代码。我们需要用到 matplotlib 模块。将如下代码添加到 pla.py 中:
def plotData(dataSet):
''' (array) -> figure
Plot a figure of dataSet
'''
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('Linear separable data set')
plt.xlabel('X')
plt.ylabel('Y')
labels = array(dataSet[:,2])
idx_1 = where(dataSet[:,2]==1)
p1 = ax.scatter(dataSet[idx_1,0], dataSet[idx_1,1], marker='o', color='g', label=1, s=20)
idx_2 = where(dataSet[:,2]==-1)
p2 = ax.scatter(dataSet[idx_2,0], dataSet[idx_2,1], marker='x', color='r', label=2, s=20)
plt.legend(loc = 'upper right')
plt.show()matplotlib 用起来比较复杂,但是能够精确控制图像的显示。注意代码中的 where 函数是用来找出正例的行的下标,然后我们可以把正例和反例用不同的颜色和形状表示出来。如果有其他函数使用的问题,可以自行百度解决,很容易就能找到函数的用法。
下面我们来测试一下(注意,我们编写的函数 plotData 只能绘制二维图像,所以我们需要产生只有两个特征的数据集。如果你想绘制三维图像,可以自己摸索一下)。因为在 pla.py 中添加了新代码,所以首先要重新加载我们的模块:
>>> reload(pla)
输入如下命令以产生 100 个数据点:
>>> data = pla.makeLinearSeparableData([4,3],100)
然后输入如下命令绘制散点图(参数为我们产生的数据集):
>>> pla.plotData(data)
如图所示:
绘制的散点图如下图所示:
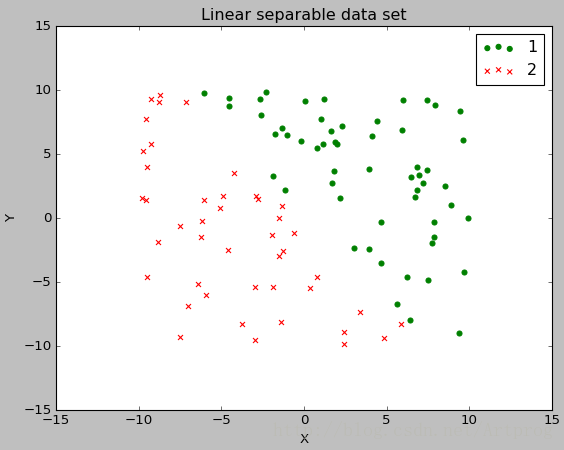
可以看到,我们产生的随机的数据集合是没有问题的,是线性可分的。
训练感知机,可视化分类器及其法向量
已经有了线性可分的数据,接下来,我们就可训练感知机了。将如下代码添加到 pla.py 中:
def train(dataSet, plot = False):
''' (array, boolean) -> list
Use dataSet to train a perceptron
dataSet has at least 2 lines.
'''
numLines = dataSet.shape[0]
numFeatures = dataSet.shape[1]
w = zeros((1, numFeatures - 1)) # initialize weights
separated = False
i = 0;
while not separated and i < numLines:
if dataSet[i][-1] * sum(w * dataSet[i,0:-1]) <= 0:
w = w + dataSet[i][-1] * dataSet[i,0:-1]
separated = False
i = 0;
else:
i += 1
if plot == True:
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('Linear separable data set')
plt.xlabel('X')
plt.ylabel('Y')
labels = array(dataSet[:,2])
idx_1 = where(dataSet[:,2]==1)
p1 = ax.scatter(dataSet[idx_1,0], dataSet[idx_1,1],
marker='o', color='g', label=1, s=20)
idx_2 = where(dataSet[:,2]==-1)
p2 = ax.scatter(dataSet[idx_2,0], dataSet[idx_2,1],
marker='x', color='r', label=2, s=20)
x = w[0][0] / abs(w[0][0]) * 10
y = w[0][1] / abs(w[0][0]) * 10
ann = ax.annotate(u"",xy=(x,y),
xytext=(0,0),size=20, arrowprops=dict(arrowstyle="-|>"))
ys = (-12 * (-w[0][0]) / w[0][1], 12 * (-w[0][0]) / w[0][1])
ax.add_line(Line2D((-12, 12), ys, linewidth=1, color='blue'))
plt.legend(loc = 'upper right')
plt.show()
return w代码解释:
该函数有两个参数,地一个是数据集
dataSet,第二个是plot,如果不提供值,有默认值False,意思是只返回最后的结果,不绘制散点图。我这样设计这个训练函数,是为了方便查看训练完成后的结果。首先获得数据集的行数
numLines和特征的数目numFeatures,减一是因为最后一列是数据点的分类标签,分类标签并不是特征。创建一个数组
w保存权重向量。while循环只要满足任何一个条件就结束:已经完全将正例和负例分开,或者i的值超过样本的数量。其实第二个条件是不会发生的,因为感知机的训练算法是收敛的,所以一定会将数据完全分开,证明可见我的另一篇文章:感知机算法原理(PLA原理)及 Python 实现,但前提是数据集必须是线性可分的。下面的代码是训练算法的核心,即随机梯度下降:
if dataSet[i][-1] * sum(w * dataSet[i,0:-1]) <= 0: # 如果分类错误
w = w + dataSet[i][-1] * dataSet[i,0:-1] # 更新权重向量
separated = False # 设置为未完全分开
i = 0; # 重新开始便利每个数据点
else:
i += 1 # 如果分类正确,检查下一个数据点简单解释一下绘图部分的代码:
- 接下来的
if plot == True:代码块内的代码使用来绘制分类器及其法向量(权重向量)的。 - 需要解释的地方是
w是一个二位数组,所以w的第一个元素是w[0][0],第二个元素是w[0][1]。 x = w[0][0] / abs(w[0][0]) * 10和y = w[0][1] / abs(w[0][0]) * 10是为了避免求得的权重向量长度过大在散点图中无法显示,所以将它按比例缩小了。- 如下的代码用来产生两个点的 y 值,以绘制一条直线(感知机):
ys = (-12 * (-w[0][0]) / w[0][1], 12 * (-w[0][0]) / w[0][1]) annotate函数用于绘制法向量(带箭头的直线)
下面我们来测试一下:
>>> data = pla.makeLinearSeparableData([4,3],100)
>>> w = pla.train(data)
>>> w
array([[ 16.32172416, 11.54429628]])函数 train 正确返回了一个权重向量。在条用 train 函数时我并没有给第二个参数 plot 赋值,所以默认不会绘制散点图以及感知机。下面再来测试一下,并使第二个参数为 True:
w = pla.train(data, True)首先会显示散点图,关闭散点图后,才会返回权重向量 w:
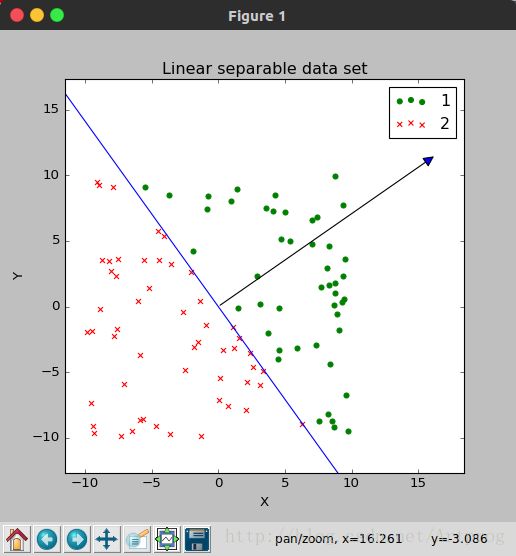
注意,如果看不见法向量(权重向量),可以使用左下角第四个按钮拖动散点图,如果发现法向量和分类器不是垂直的,是因为横纵坐标的比例不同,改变图片窗口的尺寸调整为正方形即可。
由散点图可以看出,我们的程序是正确的。另外需要注意的是我们产生数据用的权重向量 (3,4) 和我们训练得到权重向量 (16.32172416,11.54429628) 是不成比例的。为什么呢?因为随机梯度下降得到一般不是最优解,但确实可行解。
以上就是 python 实现感知机的全部内容,如有错误,请批评指正,谢谢。
声明:
本文采用 知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议 进行许可。