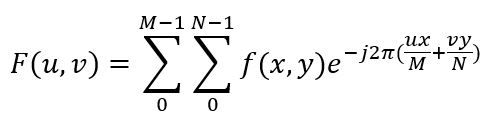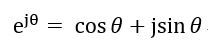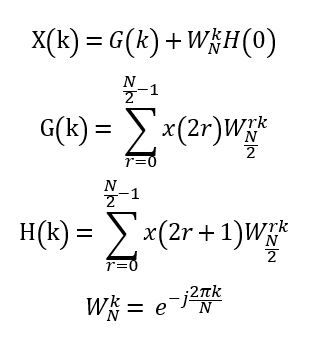二维离散傅里叶(DFT)与快速傅里叶(FFT)的实现
前言
源于图像处理与模式识别课作业。
最初接触是在大一数学分析课上,小远姐的一次大作业要求是写一篇关于傅里叶变换的应用的文章,当时有去图书馆查阅一些信号处理的书籍,第一了解到傅里叶变换。之后暑假中参与学校实验室做图像处理项目的时候,看书看到傅里叶变换,一是当时觉得太复杂了,二是所做的项目对于实时性要求较高,即便是fft可能对于3000*2000以上的图片也难以达到实时性,主要用到的边缘检测方面Sobel算法也能满足要求,所以当时也是一笔带过,没有仔细看。
这次需要作业要求手写快速傅里叶变换,才真正开始认真看这一部分内容。因为前前后后包括思考和动手写大概花了两个周的时间,在看老师课件同时也看了一下前人写的博客,自己在实现过程中也遇到过一些阻碍,不过最后还是按时交上了作业,于是把一些思路、用到相关资料和最后的代码写成一个博客,供别人参考也供自己以后参考。由于是针对图像处理,所以还是以二维变换为主。
好下面是正文。
一、离散傅里叶DFT
二维离散傅里叶DFT的公式如下:
上课的时候没有好好听,再加上高数基本上已经忘光了,第一眼看到这个公式的是懵逼的,这怎么实现,还带着自然数的指数,而且还有个 -j 是什么鬼。好吧,滚去看书。
我用的是刚萨雷斯的《数字图像处理》,从头认真看会发现作者真的是从最基础的复数将到离散傅里叶变换是怎么得来的。
此处用了一个j是通过欧拉公式:
我想它的作用就是用来表示实轴分量和虚轴分量。我们编程的时候,其实还是需要使用欧拉公式将公式(1)重新展开成含三角函数的表达式。
对于离散傅里叶的得出属于信号处理中的详细内容,我在这里就不再赘述了,不过后面如果有时间我也会继续补充。
直接使用公式暴力求解离散傅里叶的算法复杂度是相当高的——O(n^2),对于一张512×512的图片,运算量是10^10量级的,我跑了一张100×100的图片大概估计了一下可能需要两个半小时。这也恰恰说明的fft的必要性,fft的算法复杂度是O(nlogn),同样是一张512×512的图片,大概就能降到10^6量级。对于我自己写的fft差不多在30s左右orz,而使用OpenCV自带的dct()函数几乎是秒出。当然我后面给出的fft还有很多问题,用了很多vector来存储在一定程度上拖慢了速度,我也会花时间不断改进。
离散傅里叶的代码就不给出了,能来看这篇文章的人应该都能写出来一个暴力求解离散傅里叶的程序吧。
二、快速离散傅里叶FFT
快速傅里叶使用的算法叫蝶形算法,如下图所示:
这样的一个运算单元被叫做蝶形单元,emmm不得不说程序员们的脑回路真的是清奇,我为啥觉得叫沙漏算法更形象呢。(手动划掉)。老师ppt的给出的蝶形运算的图真的困扰了我很久,然后我就转去看快速傅里叶变换的公式,想甩开图直接从公式入手进行实现,公式如下:
不得不说,从看这一组公式开始,就基本入坑了,因为这个公式几乎就是在诱导你写一个自顶向下递归的程序,而且自己也先入为主的认为既然是一个从O(n^2)降为O(nlogn)的问题,而且每次分为两部分递归,当然就是写一个分而治之的算法,当然这样写是没有问题,当时因为距离ddl还有段时间,也不着急,就一点一点写,后来发现遇到很多问题。因为要涉及到复数运算,需要建一个复数结构体,然后函数递归的返回值也要是复数。当时看网上的详解蝶形算法的文章都是非常不屑的。
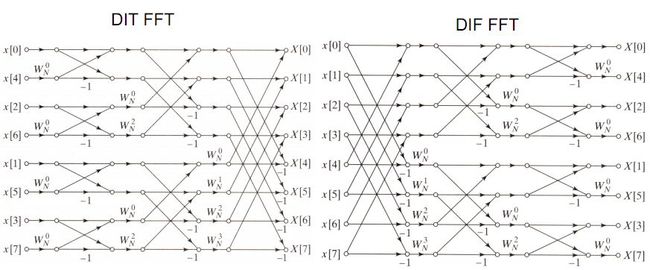
直到一天看到了这样一张图(来源点击打开链接)
突然想到,为什么不自底向上进行归并呢。可以这样想啊,我们一般用到递归向下来进行运算的时候,其实递归的底部到底有哪些值往往是不知道的或许只知道其中一部分的。但对于一维fft来说,递归底部的数据就是调整了一下顺序的某一行或者某一列,而且还具有规律(二进制倒序),我们事先其实是知道递归到哪里的、有哪些值的。那么归并其实更容易理解和实现。
一维的fft说到这里大概也就知道该怎么做了,那么既然是图像处理,当然是处理二维问题。从一维得到二维其实很简单,就是先对输入的图像(m×n)的每一行先做一维fft,把结果存到一个(m×n)的矩阵A中,再对矩阵A的每一列做fft。这时得到的结果就是二维图像(m×n)的fft。
三、fft实现代码
一下是fft的实现代码,
#define _CRT_SECURE_NO_DEPRECATE
#include
#include
#include
#include
#include
#include
#include
#include
#define PI 3.14159
using namespace cv;
using namespace std;
struct eType {
float real;
float irreal;
};
eType eMult(eType a, eType b) {
return{ a.real*b.real - a.irreal*b.irreal, a.real*b.irreal + a.irreal*b.real };
}
eType eAdd(eType a, eType b) {
return{ a.real + b.real, a.irreal + b.irreal };
}
int reverse_bit(int num, int len) //求二进制逆序数
{
int i, bit;
unsigned new_num = 0;
for (i = 0; i < len; i++)
{
bit = num & 1;
new_num <<= 1;
new_num = new_num | bit;
num >>= 1;
}
return new_num;
}
int if_binaryNum(int length) { //判断是否是2的整数次方
int num = 0;
while (length != 1) {
if (length % 2 == 0) {
length = length / 2;
num++;
}
else {
return -1;
}
}
return num;
}
Mat binarylizeImage(Mat image) { //将非2的整数次方边长的图片缩放为2的整数次方
float c = image.cols, r = image.rows;
int cn = 0, rn = 0, cnew = 2, rnew = 2;
while (c / 2 > 1) { c = c / 2; cn++;}
while (r / 2 > 1) { r = r / 2; rn++;}
while (cn > 0) { cnew = cnew * 2; cn--;}
while (rn > 0) { rnew = rnew * 2; rn--;}
resize(image, image, Size(cnew, rnew));
return image;
}
void fastFuriorTransform(Mat image) {
int lengthC = image.cols;
int lengthR = image.rows;
int numC, numR;
vector resultE;
Mat furiorResultF = Mat(image.cols, image.rows, CV_32FC1);
//映射表
vector mappingC;
vector mappingR;
//W值表
vector mappingWC;
vector mappingWR;
//判断输入图片边长是否是2的n次方,如果不符合,调整image大小
numC = if_binaryNum(lengthC);
numR = if_binaryNum(lengthR);
if (numC == -1 || numR == -1) {
fastFuriorTransform(binarylizeImage(image));
return;
}
//构造映射表
for (int c = 0; c < image.cols; c++) {
mappingC.push_back(0);
}
for (int r = 0; r < image.rows; r++) {
mappingR.push_back(0);
}
for (int c = 0; c < image.cols; c++) {
mappingC.at(reverse_bit(c, numC)) = c;
}
for (int r = 0; r < image.rows; r++) {
mappingR.at(reverse_bit(r, numR)) = r;
}
//构造W表
for (int i = 0; i < lengthC / 2; i++) {
eType w = { cosf(2 * PI / lengthC * i), -1 * sinf(2 * PI / lengthC * i) };
mappingWC.push_back(w);
}
for (int i = 0; i < lengthR / 2; i++) {
eType w = { cosf(2 * PI / lengthR * i), -1 * sinf(2 * PI / lengthR * i) };
mappingWR.push_back(w);
}
//初始化
for (int r = 0; r < lengthR; r++) {
for (int c = 0; c < lengthC; c++) {
//利用映射表,并且以0到1区间的32位浮点类型存储灰度值
eType w = { (float)image.at(mappingR.at(r), mappingC.at(c)) / 255, 0 };
resultE.push_back(w);
}
}
//循环计算每行
for (int r = 0; r < lengthR; r++) {
//循环更新resultE中当前行的数值,即按照蝶形向前层层推进
for (int i = 0; i < numC; i++) {
int combineSize = 2 << i;
vector newRow;
//按照2,4,8,16...为单位进行合并,并更新节点的值
for (int j = 0; j < lengthC; j = j + combineSize) {
int n;
for (int k = 0; k < combineSize; k++) {
if (k < (combineSize >> 1)) {
int w = k * lengthC / combineSize;
n = k + j + r*lengthC;
newRow.push_back(eAdd(resultE.at(n), eMult(resultE.at(n + (combineSize >> 1)), mappingWC.at(w))));
}
else {
int w = (k - (combineSize >> 1)) * lengthC / combineSize;
n = k + j - (combineSize >> 1) + r*lengthC;
newRow.push_back(eAdd(resultE.at(n), eMult({ -1, 0 }, eMult(resultE.at(n + (combineSize >> 1)), mappingWC.at(w)))));
}
}
}
//用newRow来更新resultE中的值
for (int j = 0; j < lengthC; j++) {
int n = j + r*lengthC;
resultE.at(n) = newRow.at(j);
}
newRow.clear();
}
}
//循环计算每列
for (int c = 0; c < lengthC; c++) {
for (int i = 0; i < numR; i++) {
int combineSize = 2 << i;
vector newColum;
for (int j = 0; j < lengthR; j = j + combineSize) {
int n;
for (int k = 0; k < combineSize; k++) {
if (k < (combineSize >> 1)) {
int w = k * lengthR / combineSize;
n = (j + k) * lengthC + c;
newColum.push_back(eAdd(resultE.at(n), eMult(resultE.at(n + (combineSize >> 1)*lengthC), mappingWR.at(w))));
}
else {
int w = (k - (combineSize >> 1)) * lengthR / combineSize;
n = (j + k - (combineSize >> 1)) * lengthC + c;
newColum.push_back(eAdd(resultE.at(n), eMult({ -1, 0 }, eMult(resultE.at(n + (combineSize >> 1)*lengthC), mappingWR.at(w)))));
}
}
}
//用newColum来更新resultE中的值
for (int j = 0; j < lengthR; j++) {
int n = j*lengthC + c;
resultE.at(n) = newColum.at(j);
}
newColum.clear();
}
}
//结果存入一个vector中
float val_max, val_min;
vector amplitude;
for (int r = 0; r < lengthR; r++) {
for (int c = 0; c < lengthC; c++) {
eType e = resultE.at(r*lengthC + c);
float val = sqrt(e.real*e.real + e.irreal*e.irreal) + 1;
//对数尺度缩放
val = log(val);
amplitude.push_back(val);
if (c == 0 && r == 0) {
val_max = val;
val_min = val;
}
else {
if (val_max < val) val_max = val;
if (val_min > val) val_min = val;
}
}
}
//将vector中的数据转存到Mat中,并归一化到0到255区间
Mat fftResult = Mat(lengthC, lengthR, CV_8UC1);
for (int i = 0; i < lengthR; i++) {
for (int j = 0; j < lengthC; j++) {
int val = (int)((amplitude.at(i*lengthC + j) - val_min) * 255 / (val_max - val_min));
fftResult.at(i, j) = val;
}
}
//调整象限
int cx = fftResult.cols / 2;
int cy = fftResult.rows / 2;
Mat q0(fftResult, Rect(0, 0, cx, cy));
Mat q1(fftResult, Rect(cx, 0, cx, cy));
Mat q2(fftResult, Rect(0, cy, cx, cy));
Mat q3(fftResult, Rect(cx, cy, cx, cy));
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);
imwrite("fft.jpg", fftResult);
imshow("fft", fftResult);
}
int main(void) {
char imagePath[256];
time_t start, end;
printf("Please input the path of the image :(No more than 255 words)\n");
//Attention, this place may have some overflow problems.
cin.getline(imagePath, 256);
Mat inputImage = imread(imagePath, 0);
while (!inputImage.data) {
printf(": Can't find this file!\n");
printf("Please input the path of the image:\n");
cin.getline(imagePath, 256);
inputImage = imread(imagePath, 0);
}
time(&start);
fastFuriorTransform(inputImage);
time(&end);
printf("Total Cost: %fs\n", difftime(end, start));
waitKey();
return 0;
} 代码中还有很多naive之处,由于主要使用vector来存储,速度差一些,后面会尝试改为指针存取,关于计算效率后面也会不断改进提高。
整个工程已经放到Github上了,点击打开链接。
致谢
首先要感谢我的导师,虽然看ppt的过程中其实困扰了我好久。
其次我还浏览其它的几篇博客,而且不敢说在他们的基础上做出来什么改进,我大概就是理解了以后自行实现。博客链接如下:
https://www.cnblogs.com/luoqingyu/p/5930181.html
https://tony4ai.com/DIP-2-4-%E4%BA%8C%E7%BB%B4FFT-IFFT-c%E8%AF%AD%E8%A8%80%E5%AE%9E%E7%8E%B0/
http://www.360doc.com/content/10/1128/20/2226925_73234298.shtml