变分贝叶斯推断(Variational Bayes Inference)简介

通常在研究贝叶斯模型中，很多情况下我们关注的是如何求解后验概率(Posterior)，不幸的是，在实际模型中我们很难通过简单的贝叶斯理论求得后验概率的公式解，但是这并不影响我们对贝叶斯模型的爱——既然无法求得精确解，来个近似解在实际中也是可以接受的:-)。一般根据近似解的求解方式可以分为随机(Stochastic)近似方法（代表是MCMC，在上一篇中我们提到的利用Gibbs Sampling训练LDA的模型便是一种），另外一种确定性(Deterministic)近似方法。本篇要介绍的变分推断便属于后者，一般情况下确定性近似方法会比随机近似方法更快和更容易判断收敛。变分贝叶斯推断是一种求解框架，类似于EM算法，在求解概率模型中有很广泛的运用，是纵横江湖不可或缺的利器:-)。本篇试图从理论上简单介绍这个方法，做到从精神上领会其脉络，具体应用例子我会给出链接，读者可以自己过过瘾:-)。

变分法(Calculus of variations)

对于普通的函数 f(x) f ( x ) ，我们可以认为 f f 是一个关于 x x 的一个实数算子，其作用是将实数 x x 映射到实数 f(x) f ( x ) ，那么可以类比这种模式，假设存在函数算子 F F ，它是关于 f(x) f ( x ) 的函数算子，可以将 f(x) f ( x ) 映射成实数 F(f(x)) F ( f ( x ) ) ，在机器学习中，常见的函数算子有信息熵 H(p(x)) H ( p ( x ) ) ，它将概率密度函数 p(x) p ( x ) 映射成一个具体值。用贴近程序语言的说法就是在变分法中，我们研究的对象是高阶函数，它接受一个函数作为参数，并返回一个值。

在求解函数 f(x) f ( x ) 极值的时候，我们利用微分法，假设它存在极小值 x0 x 0 ，那么其导数 f′(x0)=0 f ′ ( x 0 ) = 0 ，并且对于任意接近0的数 ϵ ϵ 有：

f(x0)≤f(x0+ϵ) f ( x 0 ) ≤ f ( x 0 + ϵ )

如果定义函数 Φ(ϵ)=f(x0+ϵ) Φ ( ϵ ) = f ( x 0 + ϵ ) ，那么另一种说明函数 f f 在 x0 x 0 处取得极值的说法就是：

Φ′(0)=dΦ(ϵ)dϵ∣∣∣ϵ=0=f′(x0+0)=f′(x0)=0 Φ ′ ( 0 ) = d Φ ( ϵ ) d ϵ | ϵ = 0 = f ′ ( x 0 + 0 ) = f ′ ( x 0 ) = 0

那么，类似的，如何求解一个高阶函数的极值呢？以下来源于 维基百科，由于本人对泛涵了解甚少，遂翻译之以供参考:-)。
考察如下函数算子：

J(y)=∫x2x1L(y(x),y′(x),x)dx J ( y ) = ∫ x 1 x 2 L ( y ( x ) , y ′ ( x ) , x ) d x

其中 x1,x2 x 1 , x 2 为常数， y(x) y ( x ) 是连续二阶可导， L L 对于 y,y′,x y , y ′ , x 也是连续二阶可导。
假设该函数算子 J(y) J ( y ) 在 y=f y = f 时存在极小值，那么对于任意函数 η η ，只要其满足 η(x1)=0 η ( x 1 ) = 0 且 η(x2)=0 η ( x 2 ) = 0 ，那么对于任意小的 ϵ ϵ 如下不等式成立：

J(f)≤J(f+ϵη) J ( f ) ≤ J ( f + ϵ η )

，其中 ϵη ϵ η 称为函数 f f 的变分，记为 δf δ f 。
考察函数

Φ(ϵ)=J(f+ϵη) Φ ( ϵ ) = J ( f + ϵ η )

，同样的有：

Φ′(0)=dΦ(ϵ)dϵ∣∣∣ϵ=0=dJ(f+ϵη)dϵ∣∣∣ϵ=0=∫x2x1dLdϵ∣∣∣ϵ=0dx=0 Φ ′ ( 0 ) = d Φ ( ϵ ) d ϵ | ϵ = 0 = d J ( f + ϵ η ) d ϵ | ϵ = 0 = ∫ x 1 x 2 d L d ϵ | ϵ = 0 d x = 0

其中

dLdϵ=∂L∂y∂y∂ϵ+∂L∂y′∂y′∂ϵ d L d ϵ = ∂ L ∂ y ∂ y ∂ ϵ + ∂ L ∂ y ′ ∂ y ′ ∂ ϵ

又因为 y=f+ϵη y = f + ϵ η ， y′=f′+ϵη′ y ′ = f ′ + ϵ η ′ ，因此

∂y∂ϵ=η∂y′∂ϵ=η′ ∂ y ∂ ϵ = η ∂ y ′ ∂ ϵ = η ′

代入可得：

dLdϵ=∂L∂yη+∂L∂y′η′ d L d ϵ = ∂ L ∂ y η + ∂ L ∂ y ′ η ′

，再根据 分部积分法可得：

∫x2x1dLdϵ∣∣∣ϵ=0dx=∫x2x1{∂L∂yη+∂L∂y′η′}∣∣∣ϵ=0dx=∫x2x1η{∂L∂f−ddx∂L∂f′}dx+∂L∂f′η∣∣∣x2x1=∫x2x1η{∂L∂f−ddx∂L∂f′}dx=0 ∫ x 1 x 2 d L d ϵ | ϵ = 0 d x = ∫ x 1 x 2 { ∂ L ∂ y η + ∂ L ∂ y ′ η ′ } | ϵ = 0 d x = ∫ x 1 x 2 η { ∂ L ∂ f − d d x ∂ L ∂ f ′ } d x + ∂ L ∂ f ′ η | x 1 x 2 = ∫ x 1 x 2 η { ∂ L ∂ f − d d x ∂ L ∂ f ′ } d x = 0

因为当 ϵ=0 ϵ = 0 时， y−>f y − > f ， y′−>f′ y ′ − > f ′ ，又由于 η η 在 x1,x2 x 1 , x 2 取值为0，所以 ∂L∂f′η∣∣∣x2x1=0 ∂ L ∂ f ′ η | x 1 x 2 = 0 。最后根据 变分法基本引理，我们最终可得 欧拉－拉格朗日方程：

∂L∂f−ddx∂L∂f′=0 ∂ L ∂ f − d d x ∂ L ∂ f ′ = 0

需要注意的是，欧拉－拉格朗日方程只是函数算子取得极值的必要条件，而不是充分条件，但是我们总算是对于变分法有一定的初步认识，也知道其中一个求函数算子极值的方法。

平均场定理(Mean Field Theory)

对，变分推断确实和这个定理有莫大联系，有必要稍微了解一下，免得后面一脸茫然。先看看维基百科的介绍：

In physics and probability theory, mean field theory (MFT also known as self-consistent field theory) studies the behavior of large and complex stochastic models by studying a simpler model. Such models consider a large number of small individual components which interact with each other. The effect of all the other individuals on any given individual is approximated by a single averaged effect, thus reducing a many-body problem to a one-body problem.

很遗憾，笔者对平均场理论理解无法做出直观解释，期待读者解惑。总而言之，平均场理论是用于简化复杂模型的理论，譬如对于一个概率模型:

P(x1,x2,x3,...,xn)=P(x1)P(x2|x1)P(x3|x2,x1)...P(xn|xn−1,xn−2,xn−3,...,x1) P ( x 1 , x 2 , x 3 , . . . , x n ) = P ( x 1 ) P ( x 2 | x 1 ) P ( x 3 | x 2 , x 1 ) . . . P ( x n | x n − 1 , x n − 2 , x n − 3 , . . . , x 1 )

利用平均场理论我们可以找出另一个模型:

Q(x1,x2,x3,...,xn)=Q(x1)Q(x2)Q(x3)...Q(xn) Q ( x 1 , x 2 , x 3 , . . . , x n ) = Q ( x 1 ) Q ( x 2 ) Q ( x 3 ) . . . Q ( x n )

使得 Q Q 尽量和 P P 一致，并可以来近似代替 p(x1,x2,x3,...,xn) p ( x 1 , x 2 , x 3 , . . . , x n )

变分贝叶斯推断

在贝叶斯模型中，我们通常需要计算模型的后验概率 P(Z|X) P ( Z | X ) ，然而许多实际模型中，想要计算出 P(Z|X) P ( Z | X ) 通常是行不通的。利用平均场理论，我们通过找另一个模型 Q(Z)＝∏iQ(zi) Q ( Z ) ＝ ∏ i Q ( z i ) 来近似代替 P(Z|X) P ( Z | X ) ，这是变分贝叶斯推断的唯一假设！然后问题在于如何找出这样的模型 Q(Z) Q ( Z ) 了。

熟悉信息理论的同学应该知道，想要衡量两个概率模型有多大差异，可以利用KL-Divergence。于是我们将问题转化为如何找到 Q(Z) Q ( Z ) 使得

KL(Q||P)=∫Q(Z)logQ(Z)P(Z|X)dZ K L ( Q | | P ) = ∫ Q ( Z ) l o g Q ( Z ) P ( Z | X ) d Z

最小。我们知道KL散度是非对称的，那么为什么要用 KL(Q||P) K L ( Q | | P ) 而不是 KL(P||Q) K L ( P | | Q ) 呢？我们先看看PRML第十章里面的一副图：

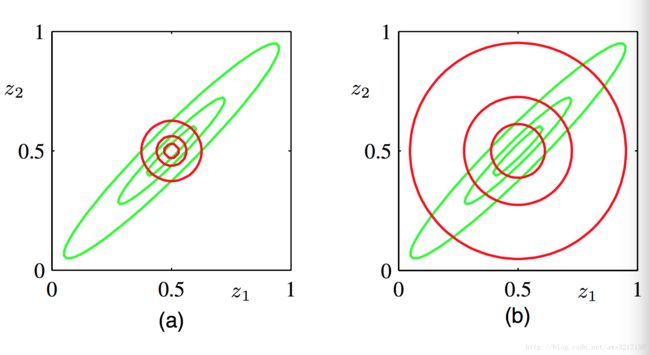
图中绿色图是 P P 的分布，图(a)红色线利用通过最小化 KL(Q||P) K L ( Q | | P ) 也就是变分推断获得的结果，图(b)红色线是通过最小化 KL(P||Q) K L ( P | | Q ) 的结果。如果选择最小化 KL(P||Q) K L ( P | | Q ) ，那么其实是对应于另外一种近似框架——Expectation Propagation，超出本篇要讨论的，暂且搁置。

那么既然我们有了目标对象——最小化 KL(Q||P) K L ( Q | | P ) ，接下来就是如何求得最小化时的 Q Q 了。我们将公式稍微变换一下：

KL(Q||P)=∫Q(Z)logQ(Z)P(Z|X)dZ=−∫Q(Z)logP(Z|X)Q(Z)dZ=−∫Q(Z)logP(Z,X)Q(Z)P(X)dZ=∫Q(Z)[logQ(Z)+logP(X)]dZ−∫Q(Z)logP(Z,X)dZ=logP(X)+∫Q(Z)logQ(Z)dZ−∫Q(Z)logP(Z,X)dZ K L ( Q | | P ) = ∫ Q ( Z ) l o g Q ( Z ) P ( Z | X ) d Z = − ∫ Q ( Z ) l o g P ( Z | X ) Q ( Z ) d Z = − ∫ Q ( Z ) l o g P ( Z , X ) Q ( Z ) P ( X ) d Z = ∫ Q ( Z ) [ l o g Q ( Z ) + l o g P ( X ) ] d Z − ∫ Q ( Z ) l o g P ( Z , X ) d Z = l o g P ( X ) + ∫ Q ( Z ) l o g Q ( Z ) d Z − ∫ Q ( Z ) l o g P ( Z , X ) d Z

令 L(Q)=∫Q(Z)logP(Z,X)dZ−∫Q(Z)logQ(Z)dZ L ( Q ) = ∫ Q ( Z ) l o g P ( Z , X ) d Z − ∫ Q ( Z ) l o g Q ( Z ) d Z ，
那么有：

logP(X)=KL(Q||P)+L(Q) l o g P ( X ) = K L ( Q | | P ) + L ( Q )

我们目标是最小化 KL(Q||P) K L ( Q | | P ) ，由于 logP(X) l o g P ( X ) 不依赖于 Z Z 的数据似然函数，可以当作是常数。那么为了最小化 KL(Q||P) K L ( Q | | P ) ，反过来我们可以最大化 L(Q) L ( Q ) ，所以我们的目标可以转移为：

max L(Q) m a x   L ( Q )

因为 KL(Q||P)≥0 K L ( Q | | P ) ≥ 0 那么有

logP(X)≥L(Q) l o g P ( X ) ≥ L ( Q )

所以 L(Q) L ( Q ) 可以看成是 logP(X) l o g P ( X ) 的下界，通常称为：ELOB(Evidence Lower Bound)。也就是我们通过最大化对数数据似然函数 logP(X) l o g P ( X ) 的下界来逼近对数似然函数的 logP(X) l o g P ( X ) 。

好，现在目标函数是：

L(Q)=∫Q(Z)logP(Z,X)dZ−∫Q(Z)logQ(Z)dZ L ( Q ) = ∫ Q ( Z ) l o g P ( Z , X ) d Z − ∫ Q ( Z ) l o g Q ( Z ) d Z

平均场定理的假设为：

Q(Z)=∏iQ(zi) Q ( Z ) = ∏ i Q ( z i )

先来等式右边后半部分：

∫Q(Z)logQ(Z)dZ＝∫∏iQ(zi)log∏jQ(zj)dZ＝∫∏iQ(zi)∑jlogQ(zj)dZ=∑j∫∏iQ(zi)logQ(zj)dZ＝∑j∫Q(zj)logQ(zj)dzj∫∏i:i≠jQ(zi)dzi=∑j∫Q(zj)logQ(zj)dzj ∫ Q ( Z ) l o g Q ( Z ) d Z ＝ ∫ ∏ i Q ( z i ) l o g ∏ j Q ( z j ) d Z ＝ ∫ ∏ i Q ( z i ) ∑ j l o g Q ( z j ) d Z = ∑ j ∫ ∏ i Q ( z i ) l o g Q ( z j ) d Z ＝ ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j ∫ ∏ i : i ≠ j Q ( z i ) d z i = ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j

神奇吧，仅仅有了平均场理论，我们便可将原本高维的复杂概率函数 Q(Z) Q ( Z ) 拆分成单变量形式。此处的变换需要注意的记号是 dZ=∏idzi d Z = ∏ i d z i ，而不是代表对向量的微分，并且注意到 ∫Q(zi)dzi=1 ∫ Q ( z i ) d z i = 1 ，因此 ∫∏i:i≠jQ(zi)dzi=∏i:i≠j∫Q(zi)dzi=1 ∫ ∏ i : i ≠ j Q ( z i ) d z i = ∏ i : i ≠ j ∫ Q ( z i ) d z i = 1 。

再来看看另外一部分：

∫Q(Z)logP(Z,X)dZ=∫∏iQ(zi)logP(Z,X)dZ=∫Q(zj)(∏i:i≠jQ(zi)logP(Z,X)dzi)dzj=∫Q(zj)Ei≠j[logP(Z,X)]dzj=∫Q(zj)log{exp(Ei≠j[logP(Z,X)])}dzj=∫Q(zj)logexp(Ei≠j[logP(Z,X)])∫exp(Ei≠j[logP(Z,X)])dzj−C=∫Q(zj)logQ∗(zj)dzj−C ∫ Q ( Z ) l o g P ( Z , X ) d Z = ∫ ∏ i Q ( z i ) l o g P ( Z , X ) d Z = ∫ Q ( z j ) ( ∏ i : i ≠ j Q ( z i ) l o g P ( Z , X ) d z i ) d z j = ∫ Q ( z j ) E i ≠ j [ l o g P ( Z , X ) ] d z j = ∫ Q ( z j ) l o g { e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) } d z j = ∫ Q ( z j ) l o g e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) ∫ e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) d z j − C = ∫ Q ( z j ) l o g Q ∗ ( z j ) d z j − C

合并两部分，可得：

L(Q)=∫Q(zj)logQ∗(zj)dzj−∑j∫Q(zj)logQ(zj)dzj−C=∫Q(zj)logQ∗(zj)Q(zj)dzj−∑i:i≠j∫Q(zi)logQ(zi)dzi−C＝−KL(Q(zj)||Q∗(zj))+∏i:i≠jH(Q(zi))−C L ( Q ) = ∫ Q ( z j ) l o g Q ∗ ( z j ) d z j − ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j − C = ∫ Q ( z j ) l o g Q ∗ ( z j ) Q ( z j ) d z j − ∑ i : i ≠ j ∫ Q ( z i ) l o g Q ( z i ) d z i − C ＝ − K L ( Q ( z j ) | | Q ∗ ( z j ) ) + ∏ i : i ≠ j H ( Q ( z i ) ) − C

其中 H(Q(zi))=−∫Q(zi)logQ(zi)dzi H ( Q ( z i ) ) = − ∫ Q ( z i ) l o g Q ( z i ) d z i 为信息熵，又由于

KL(Q(zj)||Q∗(zj))≥0 K L ( Q ( z j ) | | Q ∗ ( z j ) ) ≥ 0

并且

H(Q(zi))≥0 H ( Q ( z i ) ) ≥ 0

，那么要最大化 L(Q(Z)) L ( Q ( Z ) ) 只需要令

−KL(Q(zj)||Q∗(zj))=0 − K L ( Q ( z j ) | | Q ∗ ( z j ) ) = 0

也就是只要使得

Q(zj)=Q∗(zj)=exp(Ei≠j[logP(Z,X)])normalize constant Q ( z j ) = Q ∗ ( z j ) = e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) n o r m a l i z e   c o n s t a n t

，如果想直接用变分法求得最优解也是可以的，结合拉格朗日乘子法：

δδQ(zj){∫Q(zj)logQ∗(zj)dzj−∫Q(zj)logQ(zj)dzj+λi(∫iQ(zi)dzi−1)} δ δ Q ( z j ) { ∫ Q ( z j ) l o g Q ∗ ( z j ) d z j − ∫ Q ( z j ) l o g Q ( z j ) d z j + λ i ( ∫ i Q ( z i ) d z i − 1 ) }

经过一系列推导，最后也可以得到以上结果。
至此我们已经从理论上找到了变分贝叶斯推断的通用公式求法，如下算法便是：

• 循环直到收敛 ：
  
  • 对于每一个 Q(zj) Q ( z j ) :
  • 令 Q(zj)=Q∗(zj) Q ( z j ) = Q ∗ ( z j )

虽然从理论上推导了变分推断的框架算法，但是对于不同模型，我们必须手动推导 Q∗(zj) Q ∗ ( z j ) ，简要来说，推导变分贝叶斯模型一般分为四个步骤：

1. 确定好研究模型各个参数的的共轭先验分布如果想做full bayes model
2. 写出研究模型的联合分布 P(Z,X) P ( Z , X )
3. 根据联合分布确定变分分布的形式 Q(Z) Q ( Z )
4. 对于每个变分因子 Q(zj) Q ( z j ) 求出 P(Z,X) P ( Z , X ) 关于不包含变量 zj z j 的数学期望，再规整化为概率分布

当然这个过程并不简单，对于实际模型，其推导一般比较繁冗复杂，很容易出错，想一看究竟的同学可以参考文末中给的链接。所以后来便有学者研究出更加一般更加自动化的基于概率图模型的算法框架——VMP(Varaitional Message Passing) 。如果模型是指数族的模型，都可以套用VMP自动得到算法求解:-)。 有兴趣的同学可以参考：《variational message passing》

参考文献

《A Tutorial on Variational Bayesian Inference》
《Pattern Recognition and Machine Learning》第十章
有兴趣的同学可以目睹LDA的变分推断过程:-)
《Latent Dirichlet Allocation》