条件随机场(Conditional Random Field)简介

条件随机场(CRF)由Lafferty等人于2001年提出，是一种判别式概率模型，在许多自然语言处理任务中比如分词，命名实体识别等表现尤为出色。本篇与lafferty原始论文相同，将着重介绍条件随机场的一种特殊形式——线性链条件随机场(Linear Chain CRF)。

为什么需要CRF

作为Motivation，我们考虑如下词性标注任务：

对于一段输入文字“The dog barks”，我们希望获得他的词性标注“The/D(冠词) dog/N(名词) barks/V(动词)”。也就是对于一段输入序列 x⃗ =[x1,x2,....,xn] x → = [ x 1 , x 2 , . . . . , x n ] ,我们希望获得相应的特定任务的输出序列 s⃗ =[s1,s2,...,sn] s → = [ s 1 , s 2 , . . . , s n ] 。比如刚刚举的词性标注例子，此时 xn x n 将对应字典集 V V 里面的词， sn s n 则是词性集 S S 里面的元素

一个解决方案——MEMM

为了解决上述问题，一个解决思路是建立一个条件概率模型：

p(s⃗ |x⃗ ) p ( s → | x → )

McCallum等人为了解决HMM模型表达能力的局限性，于2000年提出了MEMM(Maximum Entropy Markov Model)，该模型如下：

p(s⃗ |x⃗ )=p(s1,s2,....,sn|x1,x2,...,xn)=∏i=1np(si|s1,s2,...,si−1,x1,x2,...,xn)=∏i=1np(si|si−1,x1,x2,...,xn)=∏i=1nexp(w⃗ Tf(si,si−1,x⃗ ))∑s′∈Sexp(w⃗ Tf(s′,si−1,x⃗ )) p ( s → | x → ) = p ( s 1 , s 2 , . . . . , s n | x 1 , x 2 , . . . , x n ) = ∏ i = 1 n p ( s i | s 1 , s 2 , . . . , s i − 1 , x 1 , x 2 , . . . , x n ) = ∏ i = 1 n p ( s i | s i − 1 , x 1 , x 2 , . . . , x n ) = ∏ i = 1 n e x p ( w → T f ( s i , s i − 1 , x → ) ) ∑ s ′ ∈ S e x p ( w → T f ( s ′ , s i − 1 , x → ) )

MEMM做了一个假设，就是状态的转移仅仅依赖于上一状态(这里我将标注标签称为一种状态)。在这样的假设下，转移概率被定义为：

p(si|si−1,x1,x2,...,xn)=exp(w⃗ Tf(si,si−1,x⃗ ))∑s′∈Sexp(w⃗ Tf(s′,si−1,x⃗ )) p ( s i | s i − 1 , x 1 , x 2 , . . . , x n ) = e x p ( w → T f ( s i , s i − 1 , x → ) ) ∑ s ′ ∈ S e x p ( w → T f ( s ′ , s i − 1 , x → ) )

其中 f(si,si−1,x⃗ ) f ( s i , s i − 1 , x → ) 是特征函数，作用是将当前状态和上一状态连同输入映射为一个数值向量：

f(si,si−1,x⃗ )→Rd f ( s i , s i − 1 , x → ) → R d

w⃗  w → 是权重向量，是模型的参数。通过这样定义，可以很容易求解模型参数 w⃗  w → ，并用viterbi算法求出该模型下的最优序列 s⃗  s → 。

Label Bias Problem

MEMM虽然可以很优雅地解决上述问题，然而却存在一个重大缺点，也就是所谓的“标注偏好”问题。什么是标注偏好呢？那就是模型在为输入序列 x⃗  x → 打标签的时候，存在偏袒心里，会倾向于选择某些标签。且看stanford大学的一个PPT：

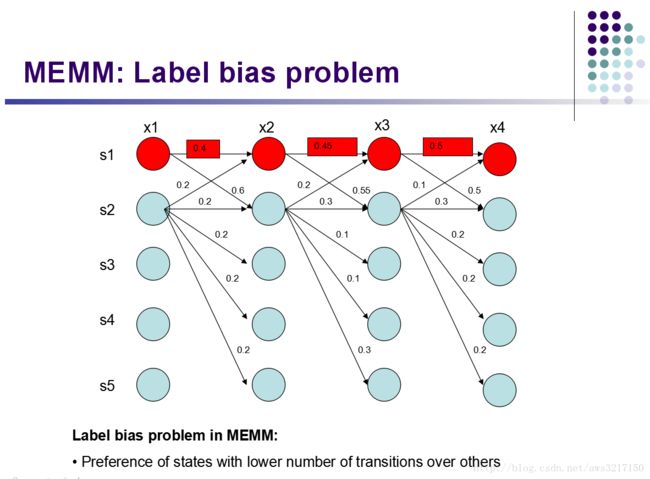
从图中可以观察，局部状态转移时， s1 s 1 倾向于转移到 s2 s 2 ，而 s2 s 2 倾向于停留在 s2 s 2 , 但是最终最好的序列却是： s1,s1,s1,s1 s 1 , s 1 , s 1 , s 1 (0.4*0.45*0.5=0.09取得最大概率！)。为什么会这样呢？注意到 s1 s 1 只有两种转移状态： s1,s2 s 1 , s 2 ，而 s2 s 2 有5种转移状态: s1,s2,s3,s4,s5 s 1 , s 2 , s 3 , s 4 , s 5 。对于 s1 s 1 的转移概率，由MEMM的定义，可得：

p(s1|s1,x⃗ )=exp(w⃗ Tf(s1,s1,x⃗ ))∑s′∈s1,s2exp(w⃗ Tf(s′,s1,x⃗ ))p(s2|s1,x⃗ )=exp(w⃗ Tf(s2,s1,x⃗ ))∑s′∈s1,s2exp(w⃗ Tf(s′,s1,x⃗ )) p ( s 1 | s 1 , x → ) = e x p ( w → T f ( s 1 , s 1 , x → ) ) ∑ s ′ ∈ s 1 , s 2 e x p ( w → T f ( s ′ , s 1 , x → ) ) p ( s 2 | s 1 , x → ) = e x p ( w → T f ( s 2 , s 1 , x → ) ) ∑ s ′ ∈ s 1 , s 2 e x p ( w → T f ( s ′ , s 1 , x → ) )

而对于 s2 s 2 的转移概率计算则是：

p(s1|s2,x⃗ )=exp(w⃗ Tf(s1,s2,x⃗ ))∑s′∈s1,...,s5exp(w⃗ Tf(s′,s2,x⃗ ))p(s2|s2,x⃗ )=exp(w⃗ Tf(s2,s2,x⃗ ))∑s′∈s1,...,s5exp(w⃗ Tf(s′,s2,x⃗ ))...p(s5|s2,x⃗ )=exp(w⃗ Tf(s5,s2,x⃗ ))∑s′∈s1,...,s5exp(w⃗ Tf(s′,s2,x⃗ )) p ( s 1 | s 2 , x → ) = e x p ( w → T f ( s 1 , s 2 , x → ) ) ∑ s ′ ∈ s 1 , . . . , s 5 e x p ( w → T f ( s ′ , s 2 , x → ) ) p ( s 2 | s 2 , x → ) = e x p ( w → T f ( s 2 , s 2 , x → ) ) ∑ s ′ ∈ s 1 , . . . , s 5 e x p ( w → T f ( s ′ , s 2 , x → ) ) . . . p ( s 5 | s 2 , x → ) = e x p ( w → T f ( s 5 , s 2 , x → ) ) ∑ s ′ ∈ s 1 , . . . , s 5 e x p ( w → T f ( s ′ , s 2 , x → ) )

说明什么问题呢？因为 s1 s 1 的转移状态很少，所以不管实际训练观测值有多少，由于每一步的状态转移概率都要归一化，所以 s1 s 1 的转移概率都会被放大，而 s2 s 2 由于转移状态多，因此每一步转移概率归一化的时候都被平均分摊了。因此在计算最优序列的时候，MEMM会偏袒那些状态转移少的标签，而忽略了实际观察值，为了说明该现象，我们再举出原始论文的例子，如下图：

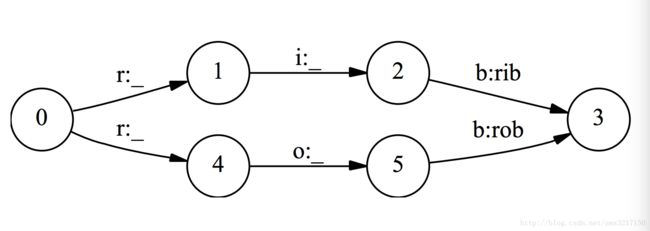
假设我们有一个辨别单词的状态机，对于单词rib和rob，从字母r出发分出两条边，经过i和o，最后到达b。对于MEMM，它对于一个单词 x x 判断是rib的概率为：

p(rib|x)=p(r|∗,x)p(i|r,x)p(b|i,x) p ( r i b | x ) = p ( r | ∗ , x ) p ( i | r , x ) p ( b | i , x )

判断为rob的概率为：

p(rob|x)=p(r|∗,x)p(o|r,x)p(b|o,x) p ( r o b | x ) = p ( r | ∗ , x ) p ( o | r , x ) p ( b | o , x )

注意到 p(b|i,x)=p(b|o,x)=1 p ( b | i , x ) = p ( b | o , x ) = 1 ,因为这些状态的转移都只有一条边，所以必然转移到下一个状态，那么只要训练数据中rob更加多，也就是 p(i|r,x)<p(o|r,x) p ( i | r , x ) < p ( o | r , x ) 那么在预测阶段，预测值将始终是rob，而不管实际观测值 x x 。

CRF

为了解决Label Bias Problem，CRF便诞生了。首先我们必须明确MEMM产生Label Bias的根源是什么，这是因为MEMM的状态转移概率的计算方式，为了获得转移概率，它每一步的状态转移都会进行归一化，从而导致问题的产生。CRF认清了问题的根源，只要不要在每一步状态转移进行归一化，而在全局进行归一化即可：

p(s⃗ |x⃗ )=exp(w⃗ TΦ(s⃗ ,x⃗ ))∑s′→∈Snexp(w⃗ TΦ(s′→,x⃗ )) p ( s → | x → ) = e x p ( w → T Φ ( s → , x → ) ) ∑ s ′ → ∈ S n e x p ( w → T Φ ( s ′ → , x → ) )

CRF相对于MEMM做了几个改动，首先在特征函数上面做了变动：

Φ(s⃗ ,x⃗ )→Rd Φ ( s → , x → ) → R d

它将输入序列 x⃗  x → 和输出标注 s⃗  s → 映射为一个d维实数向量，而MEMM的特征函数拥有的信息只是输入序列 x⃗  x → 和当前状态以及上一个状态，也就是说CRF的特征函数掌握信息量更多，从而表达能力更强。第二个的改进是它不再每一次状态转移进行归一化，而是在全局进行归一化，这样完美解决Label Bias问题。
有得必有失，注意到模型的分母需要罗列所有的状态序列，对于序列长度为 n n 的输入序列，状态序列的个数为 |S|n | S | n ，对于这种指数增长问题，在实际应用中一般都是intractable的，只能付诸于近似求解，比如我们之前提过的Variational Bayes或者Gibbs Sampling等等。不过有一种特殊结构的CRF，精确快速求解的方式是存在的，因此在早期得以广泛应用。

Linear Chain CRF

此处揭晓我们的主角——线性链CRF。熟悉概率图模型的同学可以一睹它的容貌：

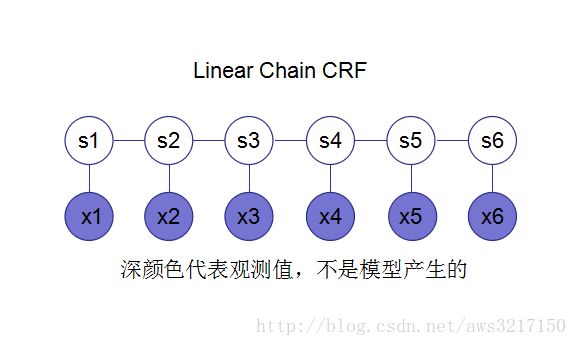
对于这样的无向图，通过定义特征函数 Φ Φ ，可以将原来intractable的问题变为tractable。我们来看看到底是如何定义的：

Φ(s⃗ ,x⃗ )=∑iϕ(si−1,si,x⃗ ) Φ ( s → , x → ) = ∑ i ϕ ( s i − 1 , s i , x → )

对于第 k k 维的特征函数值则记录为:

Φk(s⃗ ,x⃗ )=∑iϕk(si−1,si,x⃗ ) Φ k ( s → , x → ) = ∑ i ϕ k ( s i − 1 , s i , x → )

通过这样巧妙的定义： 全局特征等于局部特征的和，一切阻碍都迎刃而解！

参数估计

接下来我们介绍对于Linear Chain CRF如何进行参数参数估计的。假设我们有训练集 x1→,x2→,...,xN→ x 1 → , x 2 → , . . . , x N → ，对应的标注集合 s1→,s2→,...,sN→ s 1 → , s 2 → , . . . , s N → ，那么其对应的对数似然函数为：

L=∑iNlog p(si→|xi→)=∑iNlog exp(w⃗ TΦ(si→,xi→))∑s′→∈Snexp(w⃗ TΦ(s′→,xi→))=∑iNlog exp(∑kwkΦk(si→,xi→))∑s′→∈Snexp(∑kwkΦk(s′→,xi→)) L = ∑ i N l o g   p ( s i → | x i → ) = ∑ i N l o g   e x p ( w → T Φ ( s i → , x i → ) ) ∑ s ′ → ∈ S n e x p ( w → T Φ ( s ′ → , x i → ) ) = ∑ i N l o g   e x p ( ∑ k w k Φ k ( s i → , x i → ) ) ∑ s ′ → ∈ S n e x p ( ∑ k w k Φ k ( s ′ → , x i → ) )

对 wj w j 进行求导可得：

∂L∂wj=∑iNΦj(si→,xi→)−∑iN∑s′∈Snexp(∑kwkΦk(s′→,xi→))Φj(si→,xi→)∑s′→∈Snexp(∑kwkΦk(s′→,xi→))=∑iNΦj(si→,xi→)−∑iN∑s′→∈Snp(s′→|xi)Φj(si→,xi→) ∂ L ∂ w j = ∑ i N Φ j ( s i → , x i → ) − ∑ i N ∑ s ′ ∈ S n e x p ( ∑ k w k Φ k ( s ′ → , x i → ) ) Φ j ( s i → , x i → ) ∑ s ′ → ∈ S n e x p ( ∑ k w k Φ k ( s ′ → , x i → ) ) = ∑ i N Φ j ( s i → , x i → ) − ∑ i N ∑ s ′ → ∈ S n p ( s ′ → | x i ) Φ j ( s i → , x i → )

问题出现在上面减号的右半部分，我们单独讨论(为了记号方便，我们省去上标 i i )：

∑s⃗ ∈Snp(s⃗ |x)Φj(s⃗ ,x⃗ )=∑s⃗ ∈Snp(s⃗ |x)∑kϕj(sk−1,sk,x⃗ )=∑k∑s⃗ ∈Snp(s⃗ |x)ϕj(sk−1,sk,x⃗ )=∑k∑a∈S,b∈Sϕj(sk−1=a,sk=b,x⃗ )∑s⃗ ∈Sn,sk=b,sk−1=ap(s⃗ |x⃗ ) ∑ s → ∈ S n p ( s → | x ) Φ j ( s → , x → ) = ∑ s → ∈ S n p ( s → | x ) ∑ k ϕ j ( s k − 1 , s k , x → ) = ∑ k ∑ s → ∈ S n p ( s → | x ) ϕ j ( s k − 1 , s k , x → ) = ∑ k ∑ a ∈ S , b ∈ S ϕ j ( s k − 1 = a , s k = b , x → ) ∑ s → ∈ S n , s k = b , s k − 1 = a p ( s → | x → )

现在问题在于对于任意 a,b a , b 我们是否能快速求解

∑s⃗ ∈Sn,sk=b,sk−1=ap(s1,s2,...,si−1,si,...,sn|x⃗ )=∑s⃗ ∈Sn,sk=b,sk−1=ap(s1,s2,...,sk−1,sk,...,sn|x⃗ )=p(sk−1=a,sk=b|x⃗ ) ∑ s → ∈ S n , s k = b , s k − 1 = a p ( s 1 , s 2 , . . . , s i − 1 , s i , . . . , s n | x → ) = ∑ s → ∈ S n , s k = b , s k − 1 = a p ( s 1 , s 2 , . . . , s k − 1 , s k , . . . , s n | x → ) = p ( s k − 1 = a , s k = b | x → )

Forward-Backward 算法

首先对于如下概率图模型：

根据定义，我们可得：

p(s⃗ |x⃗ )=ψ(s⃗ ,x⃗ )ψ(x⃗ )=exp(w⃗ TΦ(s⃗ ,x⃗ ))∑s′→∈Snexp(w⃗ TΦ(s′→,x⃗ )) p ( s → | x → ) = ψ ( s → , x → ) ψ ( x → ) = e x p ( w → T Φ ( s → , x → ) ) ∑ s ′ → ∈ S n e x p ( w → T Φ ( s ′ → , x → ) )

因此有：

ψ(x⃗ )=∑s⃗ ∈Snexp(w⃗ TΦ(s⃗ ,x⃗ ))=∑s⃗ ∈Snexp(∑kwk∑jϕk(sj−1,sj,x⃗ ))=∑s⃗ ∈Snexp(∑j∑kwkϕk(sj−1,sj,x⃗ ))=∑s⃗ ∈Sn∏jexp(∑kwkϕk(sj−1,sj,x⃗ )) ψ ( x → ) = ∑ s → ∈ S n e x p ( w → T Φ ( s → , x → ) ) = ∑ s → ∈ S n e x p ( ∑ k w k ∑ j ϕ k ( s j − 1 , s j , x → ) ) = ∑ s → ∈ S n e x p ( ∑ j ∑ k w k ϕ k ( s j − 1 , s j , x → ) ) = ∑ s → ∈ S n ∏ j e x p ( ∑ k w k ϕ k ( s j − 1 , s j , x → ) )

对于熟悉概率图模型的同学，如果我们定义：

ψ(sj−1,sj)=exp(∑kwkϕk(sj−1,sj,x⃗ )) ψ ( s j − 1 , s j ) = e x p ( ∑ k w k ϕ k ( s j − 1 , s j , x → ) )

那么 ψ(sj−1,sj) ψ ( s j − 1 , s j ) 就是链式CRF图模型的一个因子， sj−1,sj s j − 1 , s j 是其最大clique。因此：

ψ(x⃗ )=∑s1∑s2...∑sn∏j=1n+1ψ(sj−1,sj)=∑s1∑s2...∑snψ(s0=∗,s1)ψ(s1,s2)...ψ(sn−1,sn)ψ(sn,sn+1=STOP)=[∑snψ(sn,STOP)[∑sn−1ψ(sn−1,sn)...[∑s1ψ(s1,s2)[ψ(∗,s1)]...] ψ ( x → ) = ∑ s 1 ∑ s 2 . . . ∑ s n ∏ j = 1 n + 1 ψ ( s j − 1 , s j ) = ∑ s 1 ∑ s 2 . . . ∑ s n ψ ( s 0 = ∗ , s 1 ) ψ ( s 1 , s 2 ) . . . ψ ( s n − 1 , s n ) ψ ( s n , s n + 1 = S T O P ) = [ ∑ s n ψ ( s n , S T O P ) [ ∑ s n − 1 ψ ( s n − 1 , s n ) . . . [ ∑ s 1 ψ ( s 1 , s 2 ) [ ψ ( ∗ , s 1 ) ] . . . ]

如果定义

α(sk)=[∑sk−1ψ(sk−1,sk)[∑sk−2ψ(sk−2,sk−1)...[∑s1ψ(s1,s2)ψ(∗,s1)]...] α ( s k ) = [ ∑ s k − 1 ψ ( s k − 1 , s k ) [ ∑ s k − 2 ψ ( s k − 2 , s k − 1 ) . . . [ ∑ s 1 ψ ( s 1 , s 2 ) ψ ( ∗ , s 1 ) ] . . . ]

则容易得到如下动态规划方程：

α(sk)=∑sk−1ψ(sk−1,sk)α(sk−1) α ( s k ) = ∑ s k − 1 ψ ( s k − 1 , s k ) α ( s k − 1 )

因此有：

ψ(x⃗ )=α(sn+1)=∑snψ(sn,STOP)α(sn) ψ ( x → ) = α ( s n + 1 ) = ∑ s n ψ ( s n , S T O P ) α ( s n )

该动态规划方程便是forward阶段，其初始值定义为：

α(s1)=ψ(∗,s1) α ( s 1 ) = ψ ( ∗ , s 1 )

若用程序实现，伪代码如下：

# n为序列x的长度
for s in S:
    alpha(1,s) = psi(*,s)
for(m = 2; m <= n; m++):
    for s in S:
        for s' in S:
            alpha(m, s) += psi(s', s) * alpha(m-1, s')
for s in S:
    alpha(n+1, STOP) += psi(s, STOP) * alpha(n, s)

类似的有：

ψ(x⃗ )=∑s1∑s2...∑sn∏j=1n+1ψ(sj−1,sj)=∑s1∑s2...∑snψ(∗,s1)ψ(s1,s2)...ψ(sn−1,sn)ψ(sn,STOP)=[∑s1ψ(∗,s1)[∑s2ψ(s1,s2)...[∑sn−1ψ(sn−2,sn−1)[∑snψ(sn−1,sn)ψ(sn,STOP)]...] ψ ( x → ) = ∑ s 1 ∑ s 2 . . . ∑ s n ∏ j = 1 n + 1 ψ ( s j − 1 , s j ) = ∑ s 1 ∑ s 2 . . . ∑ s n ψ ( ∗ , s 1 ) ψ ( s 1 , s 2 ) . . . ψ ( s n − 1 , s n ) ψ ( s n , S T O P ) = [ ∑ s 1 ψ ( ∗ , s 1 ) [ ∑ s 2 ψ ( s 1 , s 2 ) . . . [ ∑ s n − 1 ψ ( s n − 2 , s n − 1 ) [ ∑ s n ψ ( s n − 1 , s n ) ψ ( s n , S T O P ) ] . . . ]

如果定义

β(sk)=[∑sk+1ψ(sk,sk+1)...[∑sn−1ψ(sn−2,sn−1)[∑snψ(sn−1,sn)ψ(sn,STOP)]...] β ( s k ) = [ ∑ s k + 1 ψ ( s k , s k + 1 ) . . . [ ∑ s n − 1 ψ ( s n − 2 , s n − 1 ) [ ∑ s n ψ ( s n − 1 , s n ) ψ ( s n , S T O P ) ] . . . ]

则容易得到如下动态规划方程：

β(sk−1)=∑skψ(sk−1,sk)β(sk) β ( s k − 1 ) = ∑ s k ψ ( s k − 1 , s k ) β ( s k )

因此有：

ψ(x⃗ )=β(s0)=∑s1ψ(∗,s1)β(s1) ψ ( x → ) = β ( s 0 ) = ∑ s 1 ψ ( ∗ , s 1 ) β ( s 1 )

该动态规划方程便是backward阶段，其初始值定义为：

β(sn)=ψ(sn,STOP) β ( s n ) = ψ ( s n , S T O P )

伪代码实现如下：

＃n为序列x的长度
for s in S:
    beta(n, s) = psi(s, STOP)
for(m = n-1; m >= 1; m--):
    for s in S:
        for s' in S:
            beta(m, s) += psi(s, s') * beta(m+1, s')
for s in S:
    beta(0, *) = psi(*, s) * beta(1, s)

有上述的动态规划方程，我们可以很方便求解 α,β α , β 所对应的各个值。
对于 α,β α , β ,现在我们考察发现：

α(sk)β(sk)ψ(x⃗ )=[∑sk−1ψ(sk−1,sk)[∑sk−2ψ(sk−2,sk−1)...[∑s1ψ(s1,s2)ψ(∗,s1)]...]∗[∑sk+1ψ(sk,sk+1)...[∑sn−1ψ(sn−2,sn−1)[∑snψ(sn−1,sn)ψ(sn,STOP)]...]/ψ(x⃗ )=∑s1∑s2...∑sk−1∑sk+1...∑sn∏jψ(sj−1,sj,x⃗ )ψ(x⃗ )=p(sk|x⃗ ) α ( s k ) β ( s k ) ψ ( x → ) = [ ∑ s k − 1 ψ ( s k − 1 , s k ) [ ∑ s k − 2 ψ ( s k − 2 , s k − 1 ) . . . [ ∑ s 1 ψ ( s 1 , s 2 ) ψ ( ∗ , s 1 ) ] . . . ] ∗ [ ∑ s k + 1 ψ ( s k , s k + 1 ) . . . [ ∑ s n − 1 ψ ( s n − 2 , s n − 1 ) [ ∑ s n ψ ( s n − 1 , s n ) ψ ( s n , S T O P ) ] . . . ] / ψ ( x → ) = ∑ s 1 ∑ s 2 . . . ∑ s k − 1 ∑ s k + 1 . . . ∑ s n ∏ j ψ ( s j − 1 , s j , x → ) ψ ( x → ) = p ( s k | x → )

也既是：

p(sk|x⃗ )=α(sk)β(sk)ψ(x⃗ ) p ( s k | x → ) = α ( s k ) β ( s k ) ψ ( x → )

同理可得：

p(sk−1,sk|x⃗ )=α(sk−1)ψ(sk−1,sk)β(sk)ψ(x⃗ ) p ( s k − 1 , s k | x → ) = α ( s k − 1 ) ψ ( s k − 1 , s k ) β ( s k ) ψ ( x → )

由于能高效求出 α,β α , β ,边缘概率 p(sk−1,sk|x⃗ ) p ( s k − 1 , s k | x → ) 也可高效求出，那么我们可以精确高效地求出梯度！
只要能快速求解梯度，接下来我们就可以利用SGD或者L-BFGS对CRF进行快速参数估计。

序列推断(Inference)

现在模型参数估计已经知道如何求解了，接下来就是对于一个新的输入序列 x⃗  x → ，如何推测最优的标注序列：

argmaxs⃗ ∈Snp(