[机器学习实战] 阅读第四章

begintime:2019-05-06

训练模型

两种非常不同的模型训练方法：
·通过“闭式”方程——直接计算出最适合训练集的模型参数（也就是使训练集上的成本函数最小化的模型参数）。

·使用迭代优化的方法，即梯度下降（GD），逐渐调整模型参数直至训练集上的成本函数调至最低，最终趋同于第一种方法计算出来的模型参数。我们还会研究几个梯度下降的变体，包括批量梯度下降、小批量梯度下降以及随机梯度下降。

两种常用于分类任务的模型：Logistic回归（逻辑回归）和Softmax回归

softmax逻辑回归模型是logistic回归模型在多分类问题上的推广，在多分类问题中，类标签y可以取两个以上的值。
https://baike.baidu.com/item/softmax 逻辑回归/22689563?fr=aladdin

1 线性回归

训练模型就是设置模型参数直到模型最适应训练集的过程。

因此，首先要知道如何衡量模型对训练数据的拟合程度是还是差。 | 回归模型最常见的性能指标是均方根误差（RMSE） | 求取最小化RMSE的θ值 | 在实践中，将均方误差（MSE）最小化比最小化RMSE 更为简单，二者效果相同

1.1 公式4-3：线性回归模型的MSE成本函数

1.2 公式4-4： 标准方程

为了得到使成本函数最小θ值，有一个闭式解法——也就是一个直接得出结果的数学方程

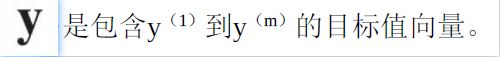
1.3 numpy.random.rand(d0, d1, …, dn)

创建一个给定形状的数组，并用[0,1]均匀分布上的随机样本填充它。

均匀分布
在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）。
https://baike.baidu.com/item/均匀分布/954451?fr=aladdin

rand(d0, d1, …, dn)

Random values in a given shape.
Create an array of the given shape and populate it with random samples from a uniform distribution over [0, 1).
d0, d1, …, dn : int, optional
The dimensions of the returned array, should all be positive. If no argument is given a single Python float is returned.
out : ndarray, shape (d0, d1, …, dn)
Random values.
random
This is a convenience function. If you want an interface that takes a shape-tuple as the first argument, refer to np.random.random_sample .

>>> np.random.rand(3,2)
array([[ 0.14022471,  0.96360618],  #random
       [ 0.37601032,  0.25528411],  #random
       [ 0.49313049,  0.94909878]]) #random
Returns:
Random values.

1.4 numpy.random.randn(d0, d1, …, dn)

填充的值为在当μ = 0,σ = 1时的正态分布（即标准正态分布）中采样的随机浮点数(如果di中的任何一个是浮点数，则首先通过截断将其转换为整数)。
如果没有提供参数，则返回从分布中随机抽样的单个浮点数。
这是一个方便函数。

>>>a=np.random.randn(10,1)
out:
[[ 1.96644911]
 [-0.14036526]
 [ 1.29307775]
 [-0.37363734]
 [-1.91293932]
 [-1.00266535]
 [ 0.64833823]
 [-0.09492032]
 [-0.98223307]
 [-0.64625605]]

1.5 numpy.linalg中的dot()、inv()、

dot()求矩阵乘
inv()求矩阵的逆

1.6 numpy.ones(shape, dtype=None, order=‘C’)

返回一个给定形状和类型的新数组，其中填充了1。
默认返回类型为float

26     Examples
27     --------
28     >>> np.ones(5)
29     array([ 1.,  1.,  1.,  1.,  1.])
30     
31     >>> np.ones((5,), dtype=np.int)
32     array([1, 1, 1, 1, 1])
33     
34     >>> np.ones((2, 1))
35     array([[ 1.],
36            [ 1.]])
37     
38     >>> s = (2,2)
39     >>> np.ones(s)
40     array([[ 1.,  1.],
41            [ 1.,  1.]])

1.7 np.r_、np.c_

np.r_是按列连接两个矩阵，就是把两矩阵上下相连，要求列数相等。
np.c_是按行连接两个矩阵，就是把两矩阵左右相连，要求行数相等。

>>>X_new=np.array([[0],[2]])
out:
[[0]
 [2]]

>>>c=np.ones((2,1))
out:
[[1.]
 [1.]]
 
>>>X_new_b=np.c_[np.ones((2,1)),X_new]#为每个实例添加x0 = 1
out:

[[1. 0.]
 [1. 2.]]

https://blog.csdn.net/weixin_41797117/article/details/80048688

endtime:2019-05-06-晚

时间紧任务重！时间就是海绵里的水，挤一挤总是会有的！
begintime：2019-05-07

2 计算复杂度

标准方程求逆的矩阵X^T*X,是一个nxn矩阵（n是特征数量）。对这种矩阵求逆的计算复杂度通常为O(n^2.4)到O(n³)之间（取决于计算实现）。

特征数量比较大时（例如100000）时，标准方程的计算极其缓慢。

截然不同的线性回归模型的训练方法，这些方法更适合特征数或者训练实例数量大到内存无法满足要求的场景。

2.1 梯度下降

通用的优化算法，为大范围的问题找到最优解。中心思想，迭代的调整参数从而使成本函数最小化。

梯度下降中一个重要参数是每一步的步长，这取决于超参数学习率。如果学习率太低（步长太小），算法需要经过大量迭代（循环）才能收敛，这将耗费大量时间。

反之，如果学习率太高，将有可能跳过全局最优解，甚至获得的结果比原来更差。这回导致算法发散，值越来越大，最后无法找到好的解决方案。

成本函数的图像复杂多样，简单些的可能是一个碗型，复杂一些的可能看着像洞、山脉、高原或者各种不规则的地形。

梯度下降的一个困难就是如何确定合适的学习率来发现全局最优解

应用梯度下降时，需要保证所有特征的大小比例都差不多（使用StandardScaler类），否则收敛的时间会长很多。

训练模型的本质

就是搜寻使成本函数（在训练机上）最小化的参数组合。这是模型参数空间层面上的搜索：模型的参数越多，这个空间的维度就越多，搜索就越难。同样是在干草堆里寻找一根针，在一个三百维的空间里就比在一个三维空间里要棘手得多。幸运的是，线性回归模型的成本函数是凸函数，针就躺在碗底。

2.2 批量梯度下降

要实现梯度下降，你需要计算每个模型关于参数θj的成本函数的梯度。换言之，你需要计算的是如果改变θj，成本函数会改变多少。这被称为偏导数。

偏导数：将y看作常量，对x求偏导；
将x看作常量，对y求偏导。

公式4-5：成本函数的偏导数

公式4-6：成本函数的梯度向量

公式4-6在计算批量梯度下降的每一步时，都是基于完整的训练集X的，每一步都使用整批训练数据。因此，在面对非常庞大的训练集时，算法会变得极慢。但是，梯度下降算法随特征数量扩展的表现比较好：如果要训练的线性模型拥有几十万个特征，使用梯度下降比标准方程要快的多。

公式4-7：梯度下降步长

2.3 使用GridSearch（）寻找学习率

要找到合适的学习率，可以使用网格搜索。但是你可能需要限制迭代次数，这样网格搜索可以淘汰掉那些收敛耗时太长的模型。

限制迭代次数的方法：
一个简单的办法是，在开始时设置一个非常大的迭代次数，但是当梯度向量的值变得很微小时中断算法——也就是当它的范数变得低于（称为容差）时，因为这时梯度下降已经（几乎）到达了最小值。

3 随机梯度下降（Stochastic Gradient Descent）

批量梯度下降的主要问题是它要用整个训练集来计算每一步的梯度，所以训练集很大时，算法会特别慢。与之相反的极端是随机梯度下降，每一步在训练集中随机选择一个实例，并且仅基于该单个实例来计算梯度。显然，这让算法变得快多了，因为每个迭代都只需要操作少量的数据。它也可以被用来训练海量的数据集，因为每次迭代只需要在内存中运行一个实例即可（SGD可以作为核外算法实现）。

另一方面，由于算法的随机性质，它比批量梯度下降要不规则得多。成本函数将不再是缓缓降低直到抵达最小值，而是不断上上下下，但是从整体来看，还是在慢慢下降。随着时间推移，最终会非常接近最小值，但是即使它到达了最小值，依旧还会持续反弹，永远不会停止。所以算法停止时获得的参数值肯定是足够好的，但不是最优的。

当成本函数非常不规则时，随机梯度下降其实可以帮助算法跳出局部最小值，所以相比批量梯度下降，它对找到全局最小值更有优势。

学习计划

因此，随机性的好处在于可以逃离局部最优，但缺点是永远定位不出最小值。要解决这个困境，有一个办法是逐步降低学习率。开始的步长比较大（这有助于快速进展和逃离局部最小值），然后越来越小，让算法尽量靠近全局最小值。这个过程叫作模拟退火，因为它类似于冶金时熔化的金属慢慢冷却的退火过程。确定每个迭代学习率的函数叫作学习计划。如果学习率降得太快，可能会陷入局部最小值，甚至是停留在走向最小值的半途中。如果学习率降得太慢，你需要太长时间才能跳到差不多最小值附近，如果提早结束训练，可能只得到一个次优的解决方案。

发现一篇很好的博客
《优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）》
https://www.cnblogs.com/guoyaohua/p/8542554.html

endtime:2019-05-07-晚

begin time:2019-05-08

4 小批量梯度下降

每一步的梯度计算，既不是基于整个训练集（如批量梯度下降）也不是基于单个实例（如随机梯度下降），而是基于一小部分随机的实例集也就是小批量。相比随机梯度下降，小批量梯度下降的主要优势在于可以从矩阵运算的硬件优化中获得显著的性能提升，特别是需要用到图形处理器时。

这个算法在参数空间层面的前进过程也不像SGD那样不稳定，特别是批量较大时。所以小批量梯度下降最终会比SGD更接近最小值一些。但是另一方面，它可能更难从局部最小值中逃脱（不是我们前面看到的线性回归问题，而是对于那些深受局部最小值陷阱困扰的问题）。

如果用好了学习计划，随机梯度下降和小批量梯度下降也同样能到达最小值。

5 多项式回归

from sklearn.preprocessing import PolynomialFeatures

一个简单的方法就是将每个特征的幂次方添加为一个新特征，然后在这个拓展过的特征集上训练线性模型。这种方法被称为多项式回归。
来拟合更复杂的数据

参数degree，阶数

PolynomialFeatures（degree=d）可以将一个包含n个特征的数组转换为包含(n+d)/(n!*d!)个特征的数组，其中n！是n的阶乘，等于1×2×3×…×n。要小心特征组合的数量爆炸。

6 学习曲线

6.1 判断模型复杂度的方法

6.1.1 方法一、使用交叉验证

使用交叉验证来评估模型的泛化性能。如果模型在训练集上表现良好，但是交叉验证的泛化表现非常糟糕，那么模型就是过度拟合。如果在二者上的表现都不佳，那就是拟合不足。这是判断模型太简单还是太复杂的一种方法。

6.1.2 方法二、观察学习曲线

这个曲线绘制的是模型在训练集和验证集上，关于“训练集大小”的性能函数。要生成这个曲线，只需要在不同大小的训练子集上多次训练模型即可。

from sklearn.metrics import mean_squared_error #从度量模块内导入计算均方误差方法 
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y): #绘制学习曲线
	X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2) #测试集占比20%
	train_errors, val_errors = [], [] #用于存放训练集均方误差、测试集均方误差
	for m in range(1, len(X_train)):  #数据集长度从1开始进行迭代
		model.fit(X_train[:m], y_train[:m]) #在不同长度的数据集上构建模型
		y_train_predict = model.predict(X_train[:m]) #对训练集进行预测
		y_val_predict = model.predict(X_val) #对验证集进行预测
		train_errors.append(mean_squared_error(y_train_predict, y_train[:m])) #将计算得到的均方误差存入列表
		val_errors.append(mean_squared_error(y_val_predict, y_val))
	plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train") #numpy.sqrt（）开平方
	plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")

注意：如果你的模型对训练数据拟合不足，添加更多训练示例也于事无补。你需要使用更复杂的模型或者找到更好的特征。

7 偏差/方差权衡

在统计学和机器学习领域，一个重要的理论结果是，模型的泛化误差可以被表示为三个截然不同的误差之和：

偏差

这部分泛化误差的原因在于错误的假设，比如假设数据是线性的，而实际上是二次的。高偏差模型最有可能对训练数据拟合不足。

方差

这部分误差是由于模型对训练数据的微小变化过度敏感导致的。具有高自由度的模型（例如高阶多项式模型）很可能也有高方差，所以很容易对训练数据过度拟合。

不可避免的误差

这部分误差是因为数据本身的噪声所致。减少这部分误差的唯一方法就是清理数据（例如修复数据源，如损坏的传感器，或者是检测并移除异常值）。增加模型的复杂度通常会显著提升模型的方差，减少偏差。反过来，降低模型的复杂度则会提升模型的偏差，降低方差。这就是为什么称其为权衡。

8 正则线性模型

减少过度拟合的一个好办法就是对模型正则化（即约束它）：它拥有的自由度越低，就越不容易过度拟合数据。比如，将多项式模型正则化的简单方法就是降低多项式的阶数。

岭回归（Ridge Regression）、套索回归（Lasso Regression）及弹性网络（Elastic Net）这三种不同的实现方法对权重进行约束。

8.1 岭回归（Ridge Regression）

公式4-8：岭回归成本函数

公式4-9：闭式解的岭回归

8.1.1 André-Louis Cholesky的矩阵因式分解法

ridge_reg = Ridge(alpha=1, solver="cholesky")

参数solver（解决方案）

8.1.2使用随机梯度下降（SGD）实现Ridge

>>> sgd_reg = SGDRegressor(penalty="l2")
>>> sgd_reg.fit(X, y.ravel())
>>> sgd_reg.predict([[1.5]])
array([[ 1.13500145]])

超参数penalty设置的是使用正则项的类型。设为"l2"表示希望SGD在成本函数中添加一个正则项，等于权重向量的l2范数的平方的一半，即岭回归。

使用Ridge类的“sag”求解器。随机平均梯度下降（sag）是梯度下降的一种变体。

更多详细信息请参考不列颠哥伦比
亚大学Mark Schmidt等人的演示文稿Minimizing Finite Sums with the
Stochastic Average Gradient Algo‐rithm”(http://goo.gl/vxVyA2)。

8.1.3 超参数penalty 设置约束类型（惩罚项）

超参数penalty设置的是使用正则项的类型。设为"l2"表示希望SGD在成本函数中添加一个正则项，等于权重向量的l2范数的平方的一半，即岭回归。

8.2 套索回归（Lasso Regression）

线性回归的另一种正则化，叫作最小绝对收缩和选择算子回归（Least Absolute Shrinkage and Selection Operator Regression，简称Lasso回归，或套索回归）。与岭回归一样，它也是向成本函数增加一个正则项，但是它增加的是权重向量的L₁范数，而不是L₂范数的平
方的一半（参见公式4-10）。

公式4-10：Lasso回归成本函数

Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重（也就是将它们设置为零）。换句话说，Lasso回归会自动执行特征选择并输出一个稀疏模型（即只有很少的特征有非零权重）。

end time:2019-05-08-晚

begin time：2019-05-09

公式4-11：Lasso回归次梯度向量

9 弹性网络（Elastic Net）

弹性网络模型介于岭回归与Lasso回归之间。其正则项是岭回归与Lasso回归的正则项的混合，混合比例通过r来控制。当r=0时，弹性网络即等同于岭回归，而当r=1时，即相当于Lasso回归。

从公式4-12可以看出

公式4-12：弹性网络成本函数

那么，到底如何选用线性回归、岭回归、Lasso回归和弹性网络呢？通常来说，有正则化——哪怕是很小，总是比没有更可取一些。所以大多数情况下，你应该避免使用纯线性回归。岭回归是个不错的
默认选择，但是如果你觉得实际用到的特征只有少数几个，那就应该更倾向于Lasso回归或是弹性网络，因为它们会将无用特征的权重降为零。一般而言，弹性网络优于Lasso回归，因为当特征数量超过训练实例数量，又或者是几个特征强相关时，Lasso回归的表现可能非常不稳定。

10 早期停止法（一种正则化方法）

对于梯度下降这一类迭代学习的算法，还有一个与众不同的正则化方法，就是在验证误差达到最小值时停止训练，该方法叫作早期停止法。
经过一轮一轮的训练，算法不断地学习，训练集上的预测误差（RMSE）自然不断下降，同样其在验证集上的预测误差也随之下降。但是，一段时间之后，验证误差停止下降反而开始回升。这说明模型开始过度拟合训练数据。通过早期停止法，一旦验证误差达到最小值就立刻停止训练。这是一个非常简单而有效的正则化技巧，所以Geoffrey Hinton称其为“美丽的免费午餐”。

对随机梯度下降和小批量梯度下降来说，曲线没有这么平滑，所以很难知道是否已经达到最小值。一种解决方法是等验证误差超过最小值一段时间之后再停止（这时你可以确信模型不会变得更好了），然后将模型参数回滚到验证误差最小时的位置。

from sklearn.base import clone
sgd_reg = SGDRegressor(n_iter=1, warm_start=True, penalty=None,learning_rate="constant", eta0=minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
	sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off 继续上次的内容
	y_val_predict = sgd_reg.predict(X_val_poly_scaled)
	val_error = mean_squared_error(y_val_predict, y_val)
	if val_error < minimum_val_error:
		minimum_val_error = val_error
		best_epoch = epoch
		best_model = clone(sgd_reg)

https://scikit-learn.org/dev/modules/generated/sklearn.linear_model.SGDRegressor.html#sklearn.linear_model.SGDRegressor

class sklearn.linear_model.SGDRegressor(
loss=’squared_loss’, 
penalty=’l2’,   #惩罚项
alpha=0.0001, 
l1_ratio=0.15, 
fit_intercept=True, 
max_iter=1000,     #通过训练数据的最大次数(又名epoch)。它只影响fit方法中的行为，而不影响partial_fit。
tol=0.001, 
shuffle=True,     #洗牌，随机打乱数据集
verbose=0, 
epsilon=0.1, 
random_state=None, 
learning_rate=’invscaling’,  #学习率
eta0=0.01,    #“常数”、“扩展”或“自适应”计划的初始学习率。默认值是0.0，因为eta0没有被默认的“最优”调度使用。
power_t=0.25, 
early_stopping=False, 
validation_fraction=0.1, 
n_iter_no_change=5, 
warm_start=False, 
average=False
)

11 逻辑回归（Logistic Regressor）

正如第1章中提到过的，一些回归算法也可用于分类（反之亦然）。逻辑回归（Logistic回归，也称为罗吉思回归）被广泛用于估算一个实例属于某个特定类别的概率。（比如，这封电子邮件属于垃圾邮件的概率是多少？）如果预估概率超过50%，则模型预测该实例属于该类别（称为正类，标记为“1”），反之，则预测不是（也就是负类，标记为“0”）。这样它就成了一个二元分类器。

11.1 概率估算

跟线性回归模型一样，逻辑回归模型也是计算输入特征的加权和（加上偏置项），但是不同于线性回归模型直接输出结果，它输出的是结果的数理逻辑

11.1.1 公式4-13：逻辑回归模型概率估算（向量化形式）

逻辑模型（也称为罗吉特），是一个sigmoid函数（即S形），记作σ（·），它的输出为一个0到1之间的数字。定义如公式4-14和图4-21所示。

11.1.2 公式4-14：逻辑函数

公式4-15：逻辑回归模型预测

11.2 训练和成本函数

训练的目的就是设置参数向量θ，使模型对正类实例做出高概率估算（y=1），对负类实例做出低概率估算（y=0）。公式4-16所示为单个训练实例x的成本函数，正说明了这一点。

11.2.1 公式4-16：单个训练实例的成本函数

11.2.2 公式4-17：逻辑回归成本函数（log损失函数）

但是坏消息是，这个函数没有已知的闭式方程（不存在一个标准方程的等价方程）来计算出最小化成本函数的θ值。而好消息是，这是个凸函数，所以通过梯度下降（或是其他任意优化算法）保证能够
找出全局最小值（只要学习率不是太高，你又能长时间等待）。公式4-18给出了成本函数关于第j个模型参数θj的偏导数方程。

11.2.3 公式4-18：Logistic成本函数的偏导数

公式4-18与公式4-5看起来非常相似：计算出每个实例的预测误差，并将其乘以第j个特征值，然后再对所有训练实例求平均值。一旦你有了包含所有偏导数的梯度向量就可以使用梯度下降算法了。就
是这样，现在你知道如何训练逻辑模型了。对随机梯度下降，一次使用一个实例；对小批量梯度下降，一次使用一个小批量。

与其他线性模型一样，逻辑回归模型可以用L₁或L₂惩罚函数来正则化。Scikit-Learn默认添加的是L₂函数。控制Scikit-Learn的LogisticRegression模型正则化程度的超参数不是alpha（其他线性模型使用alpha），而是它的逆反：C，C的值越高，模型正则化程度越高。

11.3 Softmax回归

逻辑回归模型经过推广，可以直接支持多个类别，而不需要训练并组合多个二元分类器（如第3章所述）。这就是Softmax回归，或者叫多元逻辑回归。原理很简单：对于一个给定的实例x，Softmax回归模型首先计算出每个类别k的分数sk（x），然后对这些分数应用softmax函数（也叫归一化指数），估算出每个类别的概率。你应该很熟悉计算sk（x）分数的公式（公式4-19），因为它看起来就跟线性回归预测的方程一样。

公式4-19：类别k的Softmax分数

注意，每个类别都有自己特定的参数向量θ_k。所有这些向量通常都作为行存储在参数矩阵Θ中。计算完实例x每个类别的分数后，就可以通过Softmax函数（公式4-20）来计算分数：计算出每个分数的指数，然后对它们进行归一化处理（除以所有指数的总和）即得到，也就是实例属于类别k的概率。

公式4-20：Softmax函数

跟逻辑回归分类器一样，Softmax回归分类器将估算概率值最高的类别作为预测类别（也就是分数最高的类别），如公式4-21所示。

公式4-21：Softmax回归分类器预测

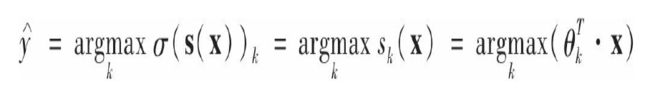
Softmax回归分类器一次只会预测一个类别（也就是说，它是多类别，但是不是多输出），所以它应该仅适用于互斥的类别之上，例如植物的不同种类。你不能用它来识别一张照片中的多个人。

既然你已经知道了模型如何进行概率估算并做出预测，那我们再来看看怎么训练。训练目标是得到一个能对目标类别做出高概率估算的模型（也就是其他类别的概率相应要很低）。通过将公式4-22的成
本函数（也叫作交叉熵）最小化来实现这个目标，因为当模型对目标类别做出较低概率的估算时，会受到惩罚。交叉熵经常被用于衡量一组估算出的类别概率跟目标类别的匹配程度（后面的章节中还会多次用到）。

公式4-22：交叉熵成本函数

交叉熵 交叉熵源于信息理论。假设你想要有效传递每天的天气信息，选项（晴、下雨等）有8个，那么你可以用3比特对每个选项进行编码，因为23=8。但是，如果你认为几乎每天都是晴天，那么，对“晴天”用1比特（0），其他七个类别用4比特（从1开始）进行编码，显然会更有效率一些。交叉熵衡量的是你每次发送天气选项的平均比特数。如果你对天气的假设是完美的，交叉熵将会等于天气本身的熵（也就是其本身固有的不可预测性）。但是如果你的假设是错误的（比如经常下雨），交叉熵将会变大，增加的这一部分我们称之为KL散度（Kullback-Leibler divergence，也叫作相对熵）。

公式4-23：对于类别k的交叉熵梯度向量

成本函数关于θ_k的梯度向量：