浅谈卡尔曼滤波(Kalman Filter)(一)
前言
在准备着考博英语复习的过程中,为了更好的与以后读博课题进行接轨,我抽出时间学习了卡尔曼滤波。首先通过查阅相关领域的教材,理解了基本的卡尔曼滤波的原理。为了巩固理解,编写了物体运动状态定位的仿真程序。随后继续研究一些常用卡尔曼滤波的变种算法。以下便是我对卡尔曼滤波算法的理解。
一.问题的引入
为了理解卡尔曼滤波算法,收集了许多资料,其中最形象的理解方式是某位吧友以传感器的例子进行类比举例。
首先,我们抛开卡尔曼滤波问题,来考虑下最简单的传感器问题。如果我们有一个传感器 A ,我们知道世界上不存在绝对精确的测量,因此 A 的测量值一定存在误差。最理想的状态是 A 的测量误差很小可以忽略不计,其测量结果可以被我们直接使用。但是现实中传感器的测量结果往往不太让人满意。假设 A 传感器测量结果是一个连续数值,且这个数值服从以下正态分布。
我们可以很容易发现,为了提高测量的质量我们可以进行多次测量然后取其平均值作为我们的最终测量结果,这样可以减少误差。假设进行两次测量,我们有以下结果。
但是有时候我们需要一个实时的测量结果。比如测量某时间点房间的气温。对于这样的问题,重复测量并不被允许,也不可能被实现。此时可以考虑再增加一个传感器,分别进行测量。然后,从直观上讲,取两个传感器的平均值来减少总体测量的误差。但是在实际中,传感器和传感器之间的误差并非完全相同,取平均值的方法并不科学。试想,如果我们有 A , B 两个传感器,其中 A 传感器的误差较小, B 传感器的误差较大,此时我们是否应该相信 A 更多一些呢?具体分析如下:
不难想象最后测量结果一定是 XA 与 XB 的线性组合。且它们的系数之和必须为1。其形式如下:
其中 k∈[0,1] 。我们只需要找到这样的一个 k , k 满足以上所有条件且使得的方差最小。令:
在极值点出可以得到:
从而有:
用 P 表示求随机变量方差的函数,将上面的式子进行调整:
通过这种方法我们可以利用两个传感器测出一个最理想的值。但是如果此时只有一个传感器怎么办?假设我们还能知道系统的方程,就可以从数学上推断出一个值,这个值与传感器得到的值不相关。我们可以把这个计算出来的值看做一个独立的传感器,然后通过以上的方法进行计算,算出最优估计值。通俗的讲,这就是卡尔曼滤波的主要思想。但是卡尔曼滤波远远比两个传感器问题要复杂的多。下面我利用一个真实的案例来简单的讲解卡尔曼滤波算法的整个过程。
二.气温测量的案例
假设我们要研究一个房间的温度,以一分钟为时间单位。
根据我们的经验判断,这个房间的温度是恒定的。但是我们对我们自己的经验并不是完全的信任,可能存在上下几度的偏差。我们需要把这个偏差看做是高斯白噪声。另外,在房间里放置一个温度计。温度计也并非完全准确,测量值会与实际值存在一定偏差。我们把这偏差也看做是高斯白噪声。现在,我们要根据以上信息来估算出房间的实际温度。
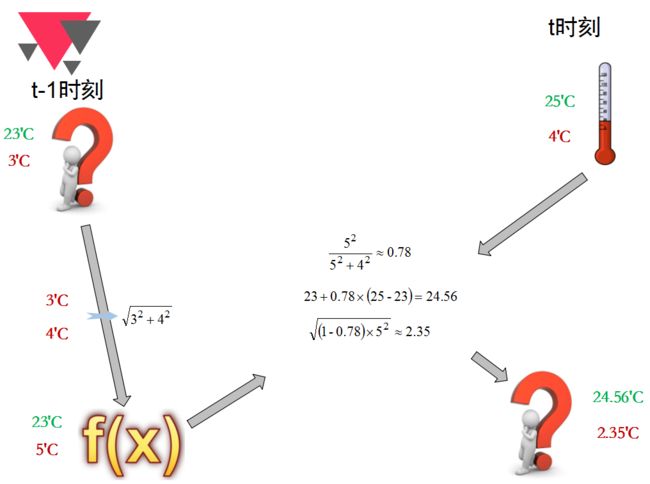
Step 1: 假设在 t−1 时刻我们预测房间的温度为23度,预测的误差为3度。假设它是服从高斯分布,我们将3度视为温度标准差。
Step 2: 根据我们的经验,在没有外界干扰的情况下房间的温度将会恒定不变。于是我们预测在 t 时刻房间的温度为23度。但是预测本身也会存在误差。我们把这个误差看做是服从高斯分布。假设其标准差为4度。值得一提的是对于4度和3度,两个高斯分布是相互独立的。综合这两个高斯分布,通过我们的经验可以得到 t 时刻的气温为23度,其标准差为5度( 5=32+42−−−−−−√ )。
Step 3: 为了更精准的测量室内温度,我们会使用温度计去测量温度。在 t 时刻温度计的读数为25度。温度计的误差为4度,其服从高斯分布。
Step 4: 此时我们对 t 时刻的气温值有两个估计,一个是人为经验的预测,另一个是温度计测量读数。它们的误差都服从高斯分布且相互独立。那么这个问题可以被视为我们之前谈到的传感器问题。
我们将其视为两个传感器然后进行加权求得我们最终的估计值。通过一系列计算,我们最终算的房间温度为24.56度,误差为2.35度。
Step 5: 将Step 4中算出的结果作为 t 时刻的最终结果,重复Step 1至Step 4便可以算出以后任意时刻房间的气温。
在这个例子中我们可以发现所有的误差都是服从高斯分布,且都相互独立。这便是卡尔曼滤波的一个先决条件。有意思的是如果我们没有温度计,一切全靠人为经验进行判断,随着不断的迭代,最终我们的估计值的误差会越来越大。如果我们只有温度计不进行人为判断,我们所测量的温度永远都会受到温度计误差的影响,特别是温度计误差过大时,我们测量值往往并不让人满意。但是同时参考人为估计和温度计测量,最终的估计值误差总能保持一个微妙的平衡。下面我们开始正式的讨论卡尔曼滤波。
三.卡尔曼滤波基本概念
卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。由于, 它便于计算机编程实现, 并能够对现场采集的数据进行实时的更新和处理,所以它是目前应用最为广泛的滤波方法, 在通信, 导航, 制导与控制等多领域得到了较好的应用。
最简单的卡尔曼滤波模型如下:
Xt 是 t 时刻我们研究对象的状态向量(温度测量的案例中状态向量维度为1)。 At,t−1 是一个矩阵,对 Xt 进行线性变换。 Zt 是 t 时刻的观测向量(温度测量的案例中温度计的读数)。 Zt 与 Xt 的维度不一定要相同。在实际运用中 Zt 往往是 Xt 中能测得的部分。 Ct 是一个矩阵。 V 是服从 N(0,R) 的高斯白噪声, W 是服从 N(0,Q) 的高斯白噪声。其满足:
δij 是克罗内克函数。
卡尔曼滤波的整个过程可以被描述为5个公式。
(1)状态的一步预测方程:
(2)均方误差的一步预测:
(3)滤波增益方程(权重):
(4)滤波估计方程(T时刻的最优值):
(5)滤波均方误差更新矩阵(T时刻的最优均方误差):
在气温测量的例子中,(1)描述的是在已知 t−1 时刻的气温,利用认为经验预测 t 时刻的气温的过程。(2)表示的是通过(1)产生的新方差,即 52=32+42 。(3)计算的是权重,即 5252+42 。通过这个权重可以决定人为预测和温度计测量值的比例。(4)表示在(3)已知的情况下计算出 t 时刻最终的估计值。(5)根据(4)计算的估计值更新方差,以便下一次迭代使用。
(1)~(5)描述的是多维数据的计算过程。现在让我们来看下它们的具体推导过程。
对于(1),它是基于一个前提 X^t−1 是 Xt−1 的无偏估计。该无偏估计的误差为 et=X^t−1−Xt−1 。此处满足 et∼N(0,Pt−1) 。所以对于(1)我们需要证明的是 X^t,t−1 是 Xt 的一个无偏估计。
基于(1)的证明过程,我们来推导(2)。
对于(3)(4)两个式子,它们关系紧密,因此我们一起进行证明。
首先我们可以设想对于我们最后的估计结果 X^t 一定是一个关于观测向量 Zt 与 t−1 时刻估计值 X^t−1 的线性方差。因此我们写成如下形式:
进一步有:
对于方差有:
对方差求迹有:
最终我们可以得到:
当我们算出估计值与对应的权重后,最后带入原始公式算出最终的方差。
至此,5个公式全部得到证明与推导。