卡尔曼滤波推导思路总结
推导思路一:
(1) 混合高斯
一维高斯函数形式:
(1) N ( x , μ , σ ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 \mathcal N(x,\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}e^-\frac{(x-\mu)^2}{2\sigma^2}\tag1 N(x,μ,σ)=σ2π1e−2σ2(x−μ)2(1)
两个高斯函数相乘(未归一化):
(2) N ( x , μ 0 , σ 0 ) × N ( x , μ 1 , σ 1 ) = ? N ( x , μ ′ , σ ′ ) \mathcal N(x,\mu_{0},\sigma_{0})\times\mathcal N(x,\mu_{1},\sigma_{1})=^?\mathcal N(x,\mu{'},\sigma{'})\tag2 N(x,μ0,σ0)×N(x,μ1,σ1)=?N(x,μ′,σ′)(2)
混合后高斯函数其均值和方差求解如下:
(3) μ ′ = μ 0 + σ 0 2 ( μ 1 − μ 0 ) σ 0 2 + σ 1 2 σ ′ 2 = σ 0 2 − σ 0 4 σ 0 2 + σ 1 2 \begin{aligned} \mu{'}&=\mu_{0}+\frac{\sigma_{0}^{2}(\mu_{1}-\mu_{0})}{\sigma_{0}^{2}+\sigma_{1}^{2}}\\ \sigma{'}^2&=\sigma_{0}^2-\frac{\sigma_{0}^4}{\sigma_{0}^{2}+\sigma_{1}^{2}} \end{aligned}\tag3 μ′σ′2=μ0+σ02+σ12σ02(μ1−μ0)=σ02−σ02+σ12σ04(3)
则上式可简化如下:
(4) k = σ 0 2 σ 0 2 + σ 1 2 μ ′ = μ 0 + k ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − k σ 0 2 \begin{aligned} k&=\frac{\sigma_{0}^2}{\sigma_{0}^{2}+\sigma_{1}^{2}}\\ \mu{'}&=\mu_{0}+k{(\mu_{1}-\mu_{0})}\\ \sigma{'}^2&=\sigma_{0}^2-k\sigma_{0}^2 \end{aligned}\tag4 kμ′σ′2=σ02+σ12σ02=μ0+k(μ1−μ0)=σ02−kσ02(4)
将上式改写为矩阵形式:
(5) K = Σ 0 ( Σ 0 + Σ 1 ) − 1 μ ⃗ ′ = u 0 ⃗ + K ( μ 1 ⃗ − u 0 ⃗ ) Σ ′ = Σ 0 − K Σ 0 \begin{aligned} K&=\Sigma_{0}(\Sigma_{0}+\Sigma_1)^{-1}\\ \vec{\mu}{'}&=\vec{u_0}+ K(\vec{\mu_1}-\vec{u_{0}})\\ \Sigma{'}&=\Sigma_{0}-K\Sigma_{0} \end{aligned}\tag{5} Kμ′Σ′=Σ0(Σ0+Σ1)−1=u0+K(μ1−u0)=Σ0−KΣ0(5)
其中 Σ i \Sigma_{i} Σi表示协方差矩阵, μ i ⃗ \vec{\mu_{i}} μi表示均值。 K K K表示卡尔曼增益。
(2)卡尔曼滤波
假定现有两个分布,一个是预测分布和观测分布:
(6) ( μ 0 , Σ 0 ) = ( H k x k ^ , H k P k H k K ) ( μ 1 , Σ 1 ) = ( z k ⃗ , R k ) \begin{aligned} (\mu_0,\Sigma_{0})&=(H_{k}\hat{x_{k}},H_kP_kH_{k}^{K})\\ (\mu_1,\Sigma_1)&=(\vec{z_{k}},R_{k}) \end{aligned}\tag6 (μ0,Σ0)(μ1,Σ1)=(Hkxk^,HkPkHkK)=(zk,Rk)(6)
结合公式5,可得如下:
(7) H k x k ′ ⃗ = H k x k ⃗ + K ( z k ⃗ − H k x k ^ ) H k P k ′ H k T = H k P k H k T − K H k P k H k T \begin{aligned} H_k\vec{x_k{'}}&=H_k\vec{x_k}+K(\vec{z_k}-H_k \hat {x_k})\\ H_kP_k{'}H_k^{T}&=H_kP_kH_k^{T}-KH_kP_kH_k^{T} \end{aligned}\tag7 Hkxk′HkPk′HkT=Hkxk+K(zk−Hkxk^)=HkPkHkT−KHkPkHkT(7)
卡尔曼增益如下:
(8) K = H k P k H k T ( H k P k H k T + R k ) − 1 K=H_kP_kH_k^{T}(H_kP_kH_k^{T}+R_k)^{-1}\tag8 K=HkPkHkT(HkPkHkT+Rk)−1(8)
式(7)、式(8)等式左右约去 H k H_k Hk,注意约去 K K K中隐藏的 H k H_k Hk,可将式(7)、式(8)写为如下:
(9) x ⃗ k ′ = x k ⃗ + K ′ ( z k ⃗ − H k x k ^ ) P k ′ = P k − K ′ H k P k K = P k H k T ( H k P k H k T + R k ) − 1 \begin{aligned} \vec{x}_k{'}&=\vec{x_k}+K{'}(\vec{z_k}-H_k \hat {x_k})\\ P_k{'}&=P_k-K{'}H_kP_k\\ K&=P_kH_k^{T}(H_kP_kH_k^{T}+R_k)^{-1} \end{aligned}\tag9 xk′Pk′K=xk+K′(zk−Hkxk^)=Pk−K′HkPk=PkHkT(HkPkHkT+Rk)−1(9)
式(9)便给了我们完整的更新步骤。
同时,我们附上一下的两个公式:
(10) x ^ k = F k x ^ k − 1 + B k μ ⃗ k P k = F k P k − 1 F k T + Q k \begin{aligned} \hat x_{k}&=F_k\hat{x}_{k-1}+B_k\vec\mu_k\\ P_k&=F_kP_{k-1}F_k^{T}+ Q_k \end{aligned}\tag{10} x^kPk=Fkx^k−1+Bkμk=FkPk−1FkT+Qk(10)
以上便是经典卡尔曼滤波中相关的5个公式。式(9)和式(10)中部分定义如下:
- H k H_k Hk为转换矩阵
- B k B_k Bk为控制矩阵
- R k R_k Rk为测量误差
- Q k Q_k Qk为系统误差
- μ ⃗ k \vec\mu_k μk为控制向量
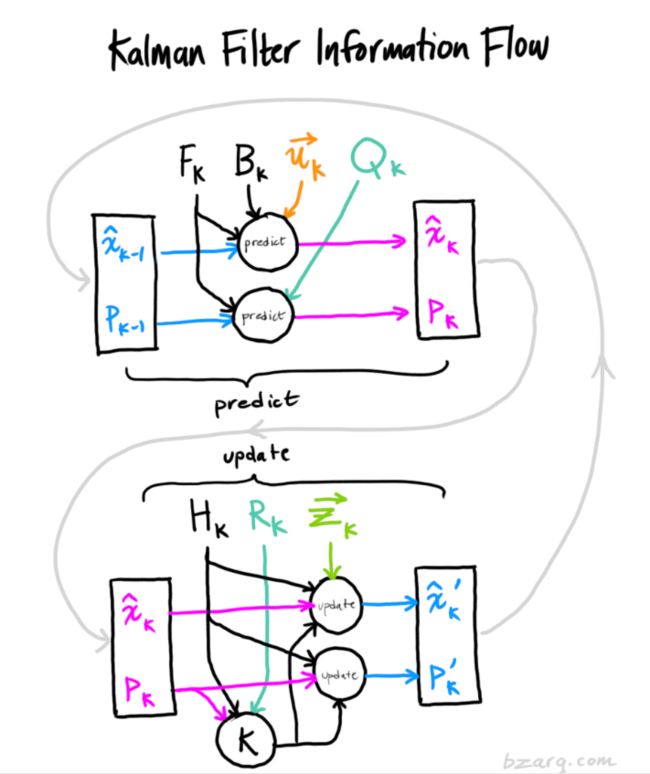
流程图如下:
推导思路一细节参见:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mjx-eqn-update
推导思路二:
由博文可知有预测方程和测量方程如下:
(1) { x k = A x k − 1 + B u k − 1 + w k − 1 z k = H x k + v k \begin{cases} x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\\ z_k=Hx_k+v_k \end{cases}\tag1 {xk=Axk−1+Buk−1+wk−1zk=Hxk+vk(1)
公式1中, A A A表示状态转换矩阵, B B B表示控制矩阵, H H H也表示转换矩阵, x k x_k xk表示预测值, z k z_k zk表示测量值, u k u_k uk表示控制向量, w k − 1 w_{k-1} wk−1表示系统噪声, v k v_k vk表示测量噪声。
针对小车加速运行问题,上式可表示为:
(2) { [ x t x ˙ t ] = [ 1 Δ t 0 1 ] [ x t − 1 x ˙ t − 1 ] + [ Δ t 2 2 Δ t ] × α z k = [ 1 0 ] [ x k x ˙ k ] \begin{cases} \begin{bmatrix} x_t\\ \dot x_t\end{bmatrix}=\begin{bmatrix}1&\Delta t \\0&1\end{bmatrix}\begin{bmatrix} x_{t-1} \\ \dot x_{t-1}\end{bmatrix}+\begin{bmatrix} \frac{\Delta t^2}{2} \\ \Delta t \end{bmatrix}\times \alpha\\ z_k=\begin{bmatrix} 1&0\end{bmatrix}\begin{bmatrix} x_k\\ \dot x_k\end{bmatrix} \end{cases}\tag2 ⎩⎪⎪⎨⎪⎪⎧[xtx˙t]=[10Δt1][xt−1x˙t−1]+[2Δt2Δt]×αzk=[10][xkx˙k](2)
公式2中 α \alpha α表示加速度。
假定系统噪声 w k w_k wk和测量噪声 v k v_k vk皆服从于高斯分布,即 p ( w ) ∼ N ( 0 , Q ) p(w)\sim N(0,Q) p(w)∼N(0,Q)和 p ( v ) ∼ N ( 0 , R ) p(v)\sim N(0,R) p(v)∼N(0,R)。以 Q = [ 0 0 0 0.01 ] Q=\begin{bmatrix}0&0\\0&0.01\end{bmatrix} Q=[0000.01]为例, Q Q Q表明系统误差的协方差速度的方差为0.01,位移上标准差为0,速度和方差之间无关联。
现有 x k ^ ′ \hat{x_k}{'} xk^′为预测值(先验), x ^ k \hat{x}_k x^k为估计值, z ^ k \hat z_k z^k为观测值(后验)。由一般的反馈思想有:
(3) x ^ k = x ^ k ′ + K k ( z k − z ^ k ) = x ^ k ′ + K k ( z k − H x ^ k ′ ) \begin{aligned} \hat x_k&=\hat x_k{'}+K_k(z_k-\hat z_k)\\&=\hat x_k{'}+K_k(z_k-H\hat x_k{'}) \end{aligned}\tag3 x^k=x^k′+Kk(zk−z^k)=x^k′+Kk(zk−Hx^k′)(3)
其中 z k z_k zk为真实值, ( z k − H x ^ k ′ ) (z_k-H\hat x_k{'}) (zk−Hx^k′)为测量值与真实值之间的残差,其中求取 K k K_k Kk为关键。
假定估计值与真实值之间的协方差为:
(4) P k = E [ e k e k T ] = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] = [ E ( S e r r S e r r T ) E ( S e r r V e r r T ) E ( V e r r S e r r T ) E ( V e r r V e r r T ) ] \begin{aligned} P_k&=E[e_ke_k^{T}]=E[(x_k-\hat x_k)(x_k-\hat x_k)^T]\\ &=\begin{bmatrix}E(S_{err}S_{err}^T)&E(S_{err}V_{err}^T)\\ E(V_{err}S_{err}^T)&E(V_{err}V_{err}^T)\end{bmatrix} \end{aligned}\tag4 Pk=E[ekekT]=E[(xk−x^k)(xk−x^k)T]=[E(SerrSerrT)E(VerrSerrT)E(SerrVerrT)E(VerrVerrT)](4)
上式中 S e r r S_{err} Serr表示位移误差, V e r r V_{err} Verr表示速度误差。
将式(3)代入式(4)得:
(5) P k = [ ( I − K k H ) ( x k − x ^ k ′ ) − K k v k ] [ ( I − K k H ) ( x k − x ^ k ′ ) − K k v k ] T P_k=[(I-K_kH)(x_k-\hat x_k{'})-K_kv_k][(I-K_kH)(x_k-\hat x_k{'})-K_kv_k]^{T}\tag{5} Pk=[(I−KkH)(xk−x^k′)−Kkvk][(I−KkH)(xk−x^k′)−Kkvk]T(5)
同理得到预测值与真实值之间的协方差。
(6) P k ′ = E [ e k ′ e k ′ T ] = E [ ( x k − x ^ k ′ ) ( x k − x ^ k ′ ) T ] P_k{'}=E[e_k{'}e_k{'}^{T}]=E[(x_k-\hat x_k{'})(x_k-\hat x_k{'})^{T}]\tag6 Pk′=E[ek′ek′T]=E[(xk−x^k′)(xk−x^k′)T](6)
注意系统状态 x k x_k xk与测量噪声 v k v_k vk之间是相互独立的。
将式(5)展开可得:
(7) P k = ( I − K k H ) E [ ( x k − x ^ k ′ ) ( x k − x ^ k ′ ) T ] ( I − K k H ) T + K k E [ v k v k T ] K k T = ( I − K k H ) P k ′ ( I − K k H ) T + K k R K k T = P k ′ − K k H P k ′ − P k ′ H T K k T + K k ( H P k ′ H T + R ) K k T \begin{aligned} P_k&=(I-K_kH)E[(x_k-\hat x_k{'})(x_k-\hat x_k{'})^{T}](I-K_kH)^{T}+K_kE[v_kv_k^{T}]K_k^{T}\\ &=(I-K_kH)P_k{'}(I-K_kH)^{T}+K_kRK_k^{T}\\ &=P_k{'}-K_kHP_k{'}-P_k{'}H^{T}K_k^{T}+K_k(HP_k{'}H^T+R)K_k^{T} \end{aligned}\tag7 Pk=(I−KkH)E[(xk−x^k′)(xk−x^k′)T](I−KkH)T+KkE[vkvkT]KkT=(I−KkH)Pk′(I−KkH)T+KkRKkT=Pk′−KkHPk′−Pk′HTKkT+Kk(HPk′HT+R)KkT(7)
结合均方差的意义,利用矩阵的迹对式(7)进行操作得:
(8) T [ P k ] = T [ P k ′ ] − 2 T [ K k H P k ′ ] + T [ K k ( H P k ′ H T + R ) K k T ] \begin{aligned} T[P_k]=T[P_k{'}]-2T[K_kHP_k{'}]+T[K_k(HP_k{'}H^T+R)K_k^{T}] \end{aligned}\tag8 T[Pk]=T[Pk′]−2T[KkHPk′]+T[Kk(HPk′HT+R)KkT](8)
最小均方差,对 K k K_k Kk进行求导,令导函数为0。则有下式:
(9) d T [ P k ] d K k = − 2 ( H P k ′ ) T + 2 K k ( H P k ′ H T + R ) = 0 ∴ K k = P k ′ H T ( H P k ′ H T + R ) − 1 \begin{aligned} \frac{dT[P_k]}{dK_k}&=-2(HP_k{'})^{T}+2K_k(HP_k^{'}H^T+R)=0\\ \therefore K_k&=P_k{'}H^{T}(HP_{k}'H^{T}+R)^{-1} \end{aligned}\tag9 dKkdT[Pk]∴Kk=−2(HPk′)T+2Kk(HPk′HT+R)=0=Pk′HT(HPk′HT+R)−1(9)
其中 R R R为测量噪声协方差矩阵。假定上面的所有维度都为 1 × 1 1\times1 1×1维,令 H = 1 H=1 H=1,且 P k ′ ≠ 0 P_{k}{'}\neq0 Pk′̸=0,则公式(9)可以简化如下:
K k = P k ′ P k ′ + R = 1 1 + R P k ′ K_k=\frac{P_k{'}}{P_k{'}+R}=\frac{1}{1+\frac{R}{P_k{'}}} Kk=Pk′+RPk′=1+Pk′R1
分析上式可得以下结论:
- 若 K k K_k Kk随着 P k ′ P_k{'} Pk′增大而增大,说明卡尔曼增益越大,越重视反馈。
- 若 P k ′ = 0 P_k{'}=0 Pk′=0,说明预测值等于真实值。
- 若 K k = 0 K_k=0 Kk=0,说明估计值等于预测值。
- 注意, P k P_k Pk为估计值与真实值之间的协方差, P k ′ P_k{'} Pk′为预测值与真实值之间的误差。
将计算出的 K k K_k Kk反代入公式 7中,化简可得:
(10) P k = P k ′ − P k ′ H T ( H P k ′ H T + R − 1 ) H P k ′ = P k ′ − K k H P k ′ = ( I − K k H ) P k ′ \begin{aligned} P_k&=P_k{'}-P_k{'}H^T(HP_k{'}H^{T}+R^{-1})HP_k{'}\\ &=P_k{'}-K_kHP_k{'}\\ &=(I-K_kH)P_k{'} \end{aligned}\tag{10} Pk=Pk′−Pk′HT(HPk′HT+R−1)HPk′=Pk′−KkHPk′=(I−KkH)Pk′(10)
上式中 P k ′ P_k{'} Pk′的递推计算如下,注意 P k ′ P_k{'} Pk′为预测值与真实值之间的协方差矩阵。
首先有预测值的递推形式: x ^ ′ k + 1 = A x k ^ + B u k \hat x{'}_{k+1}=A\hat{x_k}+Bu_k x^′k+1=Axk^+Buk,结合公式(1)可得:
(11) P ′ k + 1 = E [ e ′ k + 1 e ′ k + 1 T ] = E [ ( x k + 1 − x ^ ′ k + 1 ) ( x k + 1 − x ^ ′ k + 1 ) T ] = E [ [ A ( x k − x ^ k ) + w k ] [ A ( x k − x ^ k ) + w k ] T ] \begin{aligned} P{'}_{k+1}&=E[e{'}_{k+1}e{'}_{k+1}^{T}]=E[(x_{k+1}-\hat{x}{'}_{k+1})(x_{k+1}-\hat{x}{'}_{k+1})^{T}]\\ &=E[[A(x_k-\hat x_k)+w_k][A(x_k-\hat x_k)+w_k]^T] \end{aligned}\tag{11} P′k+1=E[e′k+1e′k+1T]=E[(xk+1−x^′k+1)(xk+1−x^′k+1)T]=E[[A(xk−x^k)+wk][A(xk−x^k)+wk]T](11)
注意系统状态 x k x_k xk和系统噪声之间相互独立。
所以公式(11)可简化如下:
(12) P ′ k + 1 = E [ ( A e k + 1 ) ( A e k + 1 ) T ] + E [ w k w k T ] = A P k A T + Q \begin{aligned} P{'}_{k+1}&=E[(Ae_{k+1})(Ae_{k+1})^{T}]+E[w_kw_k^T]\\ &=AP_kA^T+Q \end{aligned}\tag{12} P′k+1=E[(Aek+1)(Aek+1)T]+E[wkwkT]=APkAT+Q(12)
由此,也获得了 P ′ k + 1 P{'}_{k+1} P′k+1的递推公式。仅需设置最初的 P k P_k Pk,便能迭代下去。其中 Q Q Q表示系统噪声协方差矩阵。
现将卡尔曼滤波推导思路二总结如下:
(13) { x ^ k − = A x ^ k − 1 + B u k − 1 P k − = A P k − 1 A T + Q \begin{cases} \hat x_k^-=A\hat x_{k-1}+Bu_{k-1}\\ P_k^-=AP_{k-1}A^{T}+Q \end{cases}\tag{13} {x^k−=Ax^k−1+Buk−1Pk−=APk−1AT+Q(13)
由公式(13)便可计算卡尔曼增益和估计值如下:
(14) { K k = P k − H T ( H P k − H T + R ) − 1 x ^ k = x ^ k − + K k ( z k − H x k − ) \begin{cases} K_k=P_k^{-}H^T(HP_k^{-}H^T+R)^{-1}\\ \hat x_k=\hat x_k^{-}+K_k(z_k-Hx_k^{-}) \end{cases}\tag{14} {Kk=Pk−HT(HPk−HT+R)−1x^k=x^k−+Kk(zk−Hxk−)(14)
最后计算估计值和真实值之间的误差协方差矩阵为下次递推作准备:
P k = ( I − K k H ) P k − P_k=(I-K_kH)P_k^- Pk=(I−KkH)Pk−
推导思路一细节参见:https://blog.csdn.net/heyijia0327/article/details/17487467#commentBox
以上便是对卡尔曼滤波公式推导的两种总结。。。