聚类 Cluster

聚类算法评价指标
聚类性能度量可以分为两类：

• 一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”(external index)
• 一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”(internal index)

对于
外部指标
对数据集$D=\{x_1,x_2,...,x_m\}$，假定通过聚类算法将样本局为$C=\{C_1,C_2,...C_k\}$，将参考模型给出的簇划分为$C_{\ast }=\{C_1^{\ast },C_2^{\ast },...,C_S^{\ast }\}$。

相应的，另$\lambda$与${\lambda }^{\ast }$分别表示与$C$和$C^{\ast }$对应的簇标记向量。将样本两两配对考虑，有如下定义：$$a=|S_1|,S_1=\{(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j\}$$$$b=|S_2|,S_2=\{(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }̸={\lambda }_j^{\ast },i<j\}$$$$c=|S_3|,S_3=\{(x_i,x_j)|{\lambda }_i̸={\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j\}$$$$d=|S_4|,S_4=\{(x_i,x_j)|{\lambda }_i̸={\lambda }_j,{\lambda }_i^{\ast }̸={\lambda }_j^{\ast },i<j\}$$其中：
集合$S_1$表示包含了在$C$中属于相同的簇并且在$C^{\ast }$中也属于相同的簇的样本；
集合$S_2$表示包含了在$C$中属于相同的簇但在$C^{\ast }$中不属于相同的簇的样本；
……以此类推……

对每个样本对$(x_i,x_j)(i<j)$仅能出现在一个集合中，因此有$$a+b+c+d=C_m^2=\frac{m(m-1)}{2}$$基于以上定义，对无监督聚类算法的聚类结果有如下性能度量指标：

• Jaccard系数(accard Coefficient，JCI)$$JCI=\frac{a}{a+b+c}$$所有属于同一类的样本对，同时在$C$,$C^{\ast }$中隶属于同一类的样本对的比例。
• FM指数(Fowlkes and Mallows Index，FMI)$$FMI=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}$$在$C$中属于同一类的样本对中，同时属于$C$和$C^{\ast }$的样本对的比例为$p_1$；在$C^{\ast }$中属于同一类的样本对中，同时属于$C$和$C^{\ast }$的样本对的比例为$p_2$，FMI就是$p_1$和$p_2$的几何平均。
• Rand指数(Rand Index，RI)$$RI=\frac{2(a+d)}{m(m-1)}$$很显然，上述性能度量指标的取值都在$[0,1]$之间，并且取值越大越好。

内部指标
对于聚类结果$C=\{C_1,C_2,...,C_k\}$，作如下定义：$$avg(C)=\frac{2}{|C|(|C|-1)}\sum _{1⩽i⩽j⩽|C|}dist(x_i,x_j)$$$$diam(C)=\underset{1⩽i⩽j⩽|C|}{\max }dist(x_i,x_j)$$$$d_{min}(C_i,C_j)=\underset{x_i\in C_i,x_j\in C_j}{\min }dist(x_i,x_j)$$$$d_{cen}(C_i,C_j)=dist({\mu }_i,{\mu }_j)$$其中
$avg(C)$表示质心，$|C|$表示簇内样本的个数，即$|C|=k$；
$diam(C)$表示簇$C$内样本之间的最大距离；
$d_{min}(C_i,C_j)$表示簇$C_i$与簇$C_j$之间的最小距离；
$dist(x_i,x_j)$用于计算两个样本之间的距离；
$\mu$代表簇$C$的样本中心。

基于上述定义，得到如下考量聚类性能的内部指标：

• DB指数( Davies-Bouldin Index，DBI)$$DBI=\frac{1}{k}\underset{j̸=i}{\max }(\frac{avg(C_i)+avg(C_j)}{d_{cen}({\mu }_i,{\mu }_j)})$$DBI的值越小越好
• Dunn指数(Dunn Index，DI)$$DI=\underset{1⩽i⩽k}{\min }\{\underset{j̸=i}{\min }(\frac{d_{min}(C_i,C_j)}{{\max }_{1⩽l⩽k}diam(C_l)})\}$$DI的值越大越好

距离度量
聚类算法的一个重要的度量目标是表示两个样本点之间的相似程度：距离越近，相似程度越高；距离越远，相似程度越低。

常用的距离度量方式：

1. 闵可夫斯基距离；
2. 欧氏距离；
3. 曼哈顿距离；
4. 切比雪夫距离；
5. 余弦距离

其中最重要的是闵可夫斯基距离，闵可夫斯基距离是一类距离的定义。

对于$n$维空间中的两个点$x(x_1,x_2,...,x_n)$和$y(y_1,y_2,...,y_n)$，$x$、$y$两点之间的闵可夫斯基距离表示为：$$d_{xy}=\sqrt[p]{\sum _{k=1}^n(x_k-y_k{)}^p}$$其中$p$是一个可变参数。

• 当$p=1$时，称为 曼哈顿距离$$d_{xy}=\sum _{k=1}^n|x_k-y_k|$$
• 当$p=2$时，称为 欧式距离$$d_{xy}=\sqrt{\sum _{k=1}^n(x_k-y_k{)}^2}$$
• 当$p=\infty$时，称为 切比雪夫距离

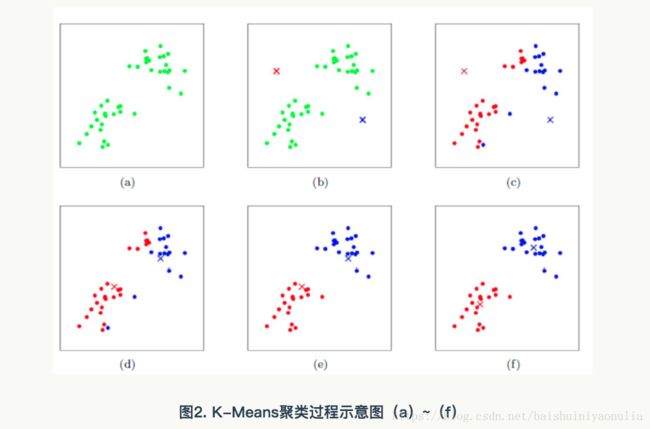
K-Means算法
对给定的样本集$D=\{x_1,x_2,...,x_m\}$，k均值算法根据聚类结果划分$C=\{C_1,C_2,...,C_k\}$
最小化平方误差：$$MSE=\sum _{i=1}^k\sum _{x\in C_i}||x-u_i|{|}_2^2$$其中$u_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$是类$C_i$的均值向量。

MSE刻画了簇类样本围绕簇均值向量的紧密程度，越小代表样本距簇均值中心越靠近。

但最优化上式的值是一个NP难的问题，因为要精确地找到它的最优解需要对样本集$D$的所有划分情况进行一一列举。

因此，K-Means算法最终采用的是贪心的策略，通过迭代优化的方式来近似求解最优MES值。

算法流程如下：
有样本集$D=\{x_1,x_2,...,x_m\}$，最终聚类的类别数$k$，最大迭代轮数$n$，前后两次迭代计算出的类标中心的距离$ϵ$

1、随机选择$k$个样本点作为类标中心

2、计算每个样本点到所有类标中心点的距离；

3、将所有样本点划分到距离最近的类标中心所在的类标；

4、重新计算每个类的类标中心；

5、重复步骤2-4，直到两次迭代计算出的类标中心不发生变化或发生的变化小于$ϵ$或者达到指定的最大迭代次数$n$。

密度聚类算法之 DBSCAN
基于密度的聚类(Density_Based Clustering)方法主要考虑的是样本分布的紧密程度，这里的紧密程度主要是用样本间的距离来衡量的。

通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连续性，并基于可连续性样本不断地扩展簇以获得最终的聚类结果。

DBSCAN是一种著名的密度聚类算法，它基于一组"领域"参数($ϵ,mps$)来刻画样本分布的紧密程度。

对给定样本集$D=\{x_1,x_2,...,x_m\}$进行如下定义：

• $ϵ$ 领域
  对于样本集$D$中的样本点$x_i$，它的$ϵ$领域定义为与$x_i$距离不大于$ϵ$的样本的集合，即$$N_{ϵ}(x_i)=\{x\in D|dist(x,x_i)⩽ϵ\}$$
• 核心对象
  如果样本$x$的$ϵ$领域内至少包含$mps$个样本，即$$|N_{ϵ}(x_i)|⩾mps$$则称$x$为核心对象
• 密度直达
  如果$x_i$是一个核心对象，并且$x_j$位于它的$ϵ$领域内
  ,那么我们称$x_j$与$x_i$密度直达
• 密度可达
  对于任意两个不同的样本点$x_i$与$x_j$，如果存在样本序列$p_1,p_2,...p_n$，其中$p_1=x_i、p_n=x_j$，且$p_{i+1}$由$p_i，i=1,2,...,n-1$密度直达，则称$x_i$与$x_j$密度可达。
• 密度相连
  对于任意的两个不同样本点$x_i$与$x_j$，如果存在第三个样本点$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$x_i$与$x_j$密度相连。
  
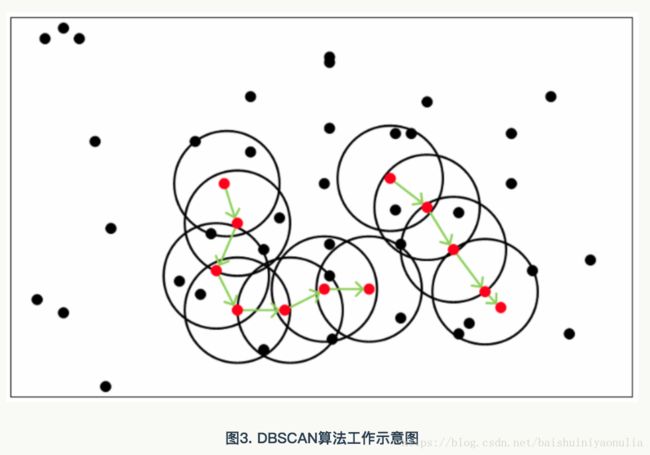
  其中：
  红点表示核心对象；黑色圆圈表示核心对象的$ϵ$领域；绿色箭头表示密度直达；绿色箭头的连线表示密度相连；绿色连线上任意两点都是密度可达。

基于以上概念的定义，那么DBSCAN中簇的定义就十分简单了：
由密度可达关系导出的最大密度相连的样本合集，即为我们最终聚类的一个簇。

形式化的定义如下：给定领域参数$(ϵ,mps)$，簇$C\subseteq D$的非空样本子集有如下性质：

• 连接性(Connectivity)
  对任意样本$x_i\in C$与$x_j\in C$有$x_i$与$x_j$密度相连；
• 最大性(Maximality)
  $x_i\in C$，且$x_j$由$x_i$有$z_j\in C$

找出簇样本合集：
DBSCAN方法任意选择一个没有类别的核心对象作为种子(Seed)，然后找到所有这个核心对象的密度可达样本集合，即为一个聚类簇。
接着继续选择另一个没有类别的核心对象去寻找密度可达的样本合集，这样就得到了另一个聚类簇。
不断循环下去，直到使用核心对象都有类别为止。

算法形式化的描述如下：

层次聚类算法之 AGNES
层次聚类（Hierarchical Clustering）是聚类算法家族中的重要的成员，它通过合并和分裂构建树状的类簇。对数据的划分主要有两种方式： 自顶向下 的分裂和 自底向上 的聚合。每棵树的根是一个聚集所有样本的独有的类。

AGNES是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看成是一个初始的聚类簇，然后在算法运行的每一步中找出距离最近的两个簇进行合并。该过程不断重复，直至达到预设的聚类簇的个数。

因此，这里的关键又是如何计算两个聚类簇之间的距离。

关于计算两个聚类簇$C_i、C_j$之间的距离，有如下四个定义式：$$d_{min}(C_i,C_j)=\underset{x_i\in C_i,x_j\in C_j}{\min }dist(x_i,x_j)$$$$d_{max}(C_i,C_j)=\underset{x_i\in C_i,x_j\in C_j}{\max }dist(x_i,x_j)$$$$d_{avg}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum _{x_i\in C_i}\sum _{x_j\in C_j}dist(x_i,x_j)$$$$d_{avg}^{\prime }(C_i,C_j)=dist(\widehat{x_i},\widehat{x_j})，\widehat{x_i}=\frac{1}{|C_i|}\sum _{k=1}^{|C_i|}{x}_k，\widehat{x_j}=\frac{1}{|C_j|}\sum _{k=1}^{|C_j|}{x}_k$$在具体的应用中，为了防止噪声点的影响，一般选择后两种距离度量方法。

AGNES聚类算法的形式化描述如下：
算法输入：

1. 训练集$D=\{x_1,x_2,...,x_m\}$
2. 类簇距离度量公式：$d(C_i,C_j)$
3. 聚类簇数目：$k$

算法输出：

1. 聚类结果划分：$C=\{C_1,C_2,...,C_k\}$

详细步骤：

for i = 1, 2,..., m:
	C_i = {x_i}
end for

for i = 1, 2,..., m:
	for j = i, i+1,..., m:
		D(i, j)=d(C_i, C_j)
		D(j, i)=D(i, j)
	end for
end for

// 初始化当前聚类簇数目
K = m

while K > k:
	find nearest class C_x C_y
	C_x = C_x cap C_y // merge into C_x
	for i = y+1, y+2,..., K:
		C_{i-1} = C_i
	end for
	delete row y and col y in D
	for j = 1, 2,..., K-1:
		D(x, j) = d(C_x, C_j)
	end for
	K = K - 1
end while