算法——排序：优先队列与堆排序

优先队列

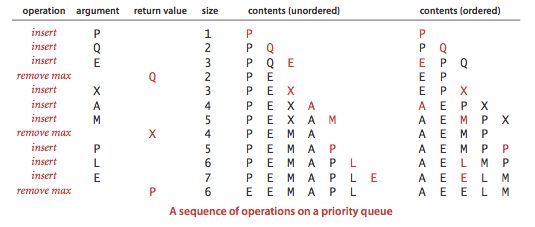
应用程序需要处理有序元素，但不需要全部有序。通常，需要收集一些元素，然后处理键值最大的元素，然后收集更多，再处理其中键值最大的元素。。。此类场景下的数据结构需要支持两种操作：移除最大元素和插入元素。这两个操作也是优先队列的特征方法。
在优先队列中，仍然通过 less() 方法比较两个元素。如果有重复元素，最大元素表示最大元素之一。

三个构造函数，可以指定队列大小，也可以通过一个数组构造PQ。
insert(Key v) 向PQ中插入一个元素
max() 返回最大元素
delMax() 删除并返回最大元素
isEmpty() 返回PQ是否为空
size() 返回PQ中的元素个数。
将 less() 比较的方向改变，即可将 MaxPQ 转化为 MinPQ。

import java.util.Stack;

/**
 * 获取最大的M个元素
 */
public class TopM {
    public void topM(int m){
        MinPQ pq = new MinPQ<>(m+1);
        while (in.hasNextLine()){
            String line = in.readLine();
            Transaction transaction = new Transaction(line);
            pq.insert(transaction);
            if (pq.size()>m){// 删除最小的，剩下的m个是目前最大的m个
                pq.delMin();
            }
        }
        Stack stack = new Stack<>();
        for (Transaction transaction:pq){
            stack.push(transaction);
        }
        for (Transaction transaction:stack){
            out.println(transaction);
        }
    }
}

class Transaction {
    public Transaction(String line) {
    }
}
class MinPQ{
    public MinPQ(int i) {}
    public void insert(T t){}
    public T delMin(){}
    public boolean isEmpty(){}
    public int size(){}
}

初级实现

• 无序数组
  插入元素的代码与栈的push方法相同。删除最大元素的代码，可以使用类似与选择排序的内循环代码，将最大元素与边界元素交换，然后删除。

public class UnorderedArrayMaxPQ> {
    private Key[] pq;      // elements
    private int n;         // number of elements
    public UnorderedArrayMaxPQ(int capacity) {
        pq = (Key[]) new Comparable[capacity];
        n = 0;
    }
    public boolean isEmpty()   { return n == 0; }
    public int size()          { return n;      }
    public void insert(Key x)  { pq[n++] = x;   }
    public Key delMax() {
        int max = 0;
        for (int i = 1; i < n; i++)
            if (less(max, i)) max = i;
        exch(max, n-1);// 将最大元素交换到最后一个位置
        return pq[--n];
    }
    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }
    private void exch(int i, int j) {
        Key swap = pq[i];
        pq[i] = pq[j];
        pq[j] = swap;
    }
}

• 有序数组
  在 insert() 方法中添加代码，将较大的元素向右移动，保持数组有序，最大元素始终在最右侧，PQ的删除最大元素和栈的 pop() 操作相同。

public class OrderedArrayMaxPQ> {
    private Key[] pq;          // elements
    private int n;             // number of elements
    public OrderedArrayMaxPQ(int capacity) {
        pq = (Key[]) (new Comparable[capacity]);
        n = 0;
    }
    public boolean isEmpty() { return n == 0;  }
    public int size()        { return n;       } 
    public Key delMax()      { return pq[--n]; }
    public void insert(Key key) {
        int i = n-1;
        while (i >= 0 && less(key, pq[i])) {
            pq[i+1] = pq[i];// 较大的元素右移，保持PQ有序
            i--;
        }
        pq[i+1] = key;
        n++;
    }
    private boolean less(Key v, Key w) {
        return v.compareTo(w) < 0;
    }
}

• 链表
  与之前类似，或者修改 pop() 方法找到并返回最大元素（无序），或者修改 push() 方法来保证有序，pop() 方法返回首元素（有序）。
  无序是惰性方法，有序则是积极方法。
  
  上述方法的插入元素或删除最大元素在最坏情况下，需要消耗线性时间。堆排序则可以使这两个操作更快（O(logN)）。

堆

当一个二叉树的每个节点都大于等于它的两个子节点（如果存在）时，该二叉树就是堆有序的。
根节点是堆有序的二叉树中的最大节点。
如果用指针表示堆有序的二叉树，每个元素都需要三个指针来找到上下节点（父节点和两个子节点）。弱使用完全二叉树，则会方便很多。

二叉堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级储存。（不使用数组的第一个位置）
即将节点按照层级放入数组中，将根节点放在位置1，它的两个子节点放在位置2和3，再子节点放在位置4,5,6和7，以此类推。

在堆中，位置 k 节点的父节点的位置为 k/2，它的两个子节点的位置为 2k 和 2k+1。
一个大小为N的完全二叉树的高度为 lgN。

堆算法

使用一个长度为 n+1 的数组 pq[] 表示大小为 n 的堆，堆元素放在 pq[1] 到 pq[n] 中，不使用 pq[0]。堆上的操作会使某个节点变大或变小，破坏堆的有序性，需要遍历堆进行修改，进而保持堆的有序性。

• 自下而上（swim）
  由于某个节点的值变大，大于父节点，我们需要将该节点与其父节点交换，交换后，该节点比两个子节点都大，一个是原父节点，另一个是原兄弟节点。该节点仍有可能大于新的父节点，我们使用类似的方法将该节点上浮，直到遇到更大的父节点，或者该节点成为根节点。
  

void swim(int k){
    while (k > 1 && less(k/2, k)){// 该节点与其父节点比较
        exch(k/2, k);// 交换该节点与父节点
        k = k/2;
    }
}

• 自上而下（sink）
  由于某个节点的值变小，小于两个子节点或小于一个子节点，我们需要将该节点与其子节点中较大的那个交换，交换后，该节点仍有可能小于子节点，我们使用类似的方法将该节点下沉，直到两个子节点都比它小，或者该节点成为叶子节点。
  

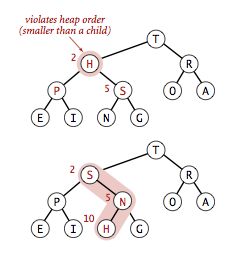
void sink(int k){
    while(2*k <= N){
        int j = 2*k;// j 为左子节点
        if (j < N && less(j, j+1)) j++;// j为较大的子节点
        if (!less(k, j)) break;// k 大于等于较大的子节点，则下沉结束
        exch(k, j); // k 下沉到较大的子节点
        k = j;
    }
}

• 插入元素
  将新元素加入堆的末尾，堆大小+1，然后该元素上浮至合适位置。
• 移除最大元素
  将根节点的最大元素移除，然后将堆的最后一个元素（不一定是最小元素）放到根节点，堆大小-1，然后根节点下沉到合适位置。

含有 n 个元素的 PQ，堆算法的插入需要不超过 1+lgn 次比较，移除最大元素需要不超过 2lgn 次比较。由于swim中有1次比较，sink中有2次比较，n个元素的层数不超过lgn。
下图中，左侧为插入元素，右侧为删除最大元素。

• 利用上浮和下沉补全MaxPQ

class MaxPQ> {
    public void insert(T t) {
        pq[++N] = t;
        swim(N);
    }

    public T delMax() {
        T max = pq[1];
        pq[1] = pq[N--];
        pq[N + 1] = null;// 记得置为null，用于GC
        sink(1);
        return max;
    }

    private void swim(int k) {// 上浮，k变小
        while (k > 1 && less(k / 2, k)) {
            exch(k, k / 2);
            k = k / 2;
        }
    }

    private void sink(int k) {// 下沉，k变大
        while (k * 2 <= N) {
            int j = k * 2;
            if (j < N && less(j, j + 1)) {
                j++;
            }
            if (!less(k, j)) {
                break;
            }
            exch(k, j);
            k = j;
        }
    }

    private T[] pq;
    private int N = 0;

    public MaxPQ(int i) {
        pq = (T[]) new Comparable[i + 1];
    }

    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }

    private void exch(int i, int j) {
        T tmp = pq[i];
        pq[i] = pq[j];
        pq[j] = tmp;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public int size() {
        return N;
    }
}

其他

Practical considerations. We conclude our study of the heap priority queue API with a few practical considerations.

• 多叉堆
  例如对于三叉树，节点k的三个子节点分别是3k-1, 3k, 3k+1，父节点是(k+1)/3。
• 调整数组大小
• 元素的不可变性
• 索引PQ

堆排序

优先队列可以发展为一种排序方法，将所有元素插入一个查找最小元素的PQ，然后不断调用 delMin() 方法，即可得到有序数组。用无序数组实现的优先队列相当于进行一次插入排序。用堆实现的，则是堆排序。
堆排序中，直接调用swim() 和 sink() 方法，将需要排序的数组本身作为堆，不需要额外的存储空间。
堆排序分为两部分：构造堆和下沉排序。构造堆过程将原始数组重新组织放入一个堆中。下沉排序过程按照降序取出元素构成排序结果。

/**
 * 堆排序
 */
public class Heap {
    public void sort(Comparable[] a) {
        int N = a.length;
        for (int k = N / 2; k >= 1; k--) {
            sink(a, k, N);// 利用下沉，构造大顶堆，父节点大于子节点
        }
        while (N > 1) {// exch和less中做了改良(i-1),所以条件是N>1,不是N>0
            exch(a, 1, N--);// 交换根（最大节点）和未排序的最后一个元素
            sink(a, 1, N);// 保持堆有序
        }
    }

    private void sink(Comparable[] a, int k, int N) {
        while (k * 2 <= N) {
            int j = k * 2;
            if (j < N && less(a, j, j + 1)) j++;
            if (!less(a, k, j)) break;
            exch(a, k, j);
            k = j;
        }
    }

    protected void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i - 1];
        a[i - 1] = a[j - 1];
        a[j - 1] = t;
    }

    private boolean less(Comparable[] a, int i, int j) {
        return a[i - 1].compareTo(a[j - 1]) < 0;
    }

    public static void main(String[] args) {
        Integer[] a = new Integer[11];
        for (int i = 0; i < a.length; i++) {
            a[i] = (int) (Math.random() * 100);
        }
        Sort.show(a);
        Heap heap = new Heap();
        heap.sort(a);
        Sort.show(a);
    }
}