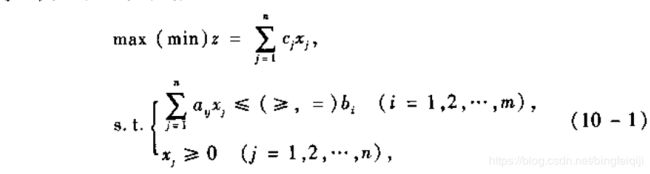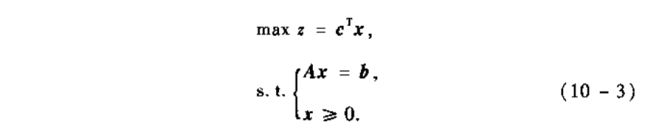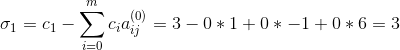单纯型法手算详解
近来看李航的《统计学习方法》的SVM的原理，暂时发现是一种线性规划问题，因此又回顾了线性规划及其解法的内容。参考《非线性最优化计算方法》张光澄版 第十章
1.线性规划模型一般形式
一般的方法为了解上述问题，因此需要对该形式化为标准形式，即对于大于或小于号，添加一个大于0的变量
，使得以下式子成立：
如例题所示：
进行求解的时候，可以随机选取几个
.等于0，使得变量数等于方程个数，也就是其他变量能够求唯一解（这个思想属于高等代数）。每个组合求一遍，就能找到所有的可能解。然后求最大值，参考https://max.book118.com/html/2016/1019/60090309.shtm，讲的很清楚，原理很简单，就是算起来比较麻烦。
2. 单纯形法
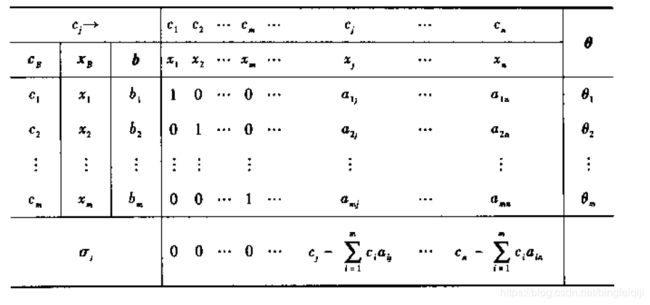
同样的，使用单纯形法，解线性规划问题，需要对格式进行改变。化为规范性，就是最上面那个目标为最大， 约束条件为等号的形式，一般来说，如果原始目标全部为小于号时，那么加上的变量应该为m个，也就是一个约束条件加一个变量，共m个约束条件，所以需要加上m个。因此，对于所有的系数能够找到一个m×m的单位阵。然后对这部分进行详细的处理、在这本书中，将单纯型法的过程浓缩为一种表的形式呈现出来，如下：
其中，c代表目标函数z里面的相应的系数，
代表的数一会给出，a就代表相应的系数。
里面的数就代表着那个m×m矩阵对应的系数。迭代过程如下：
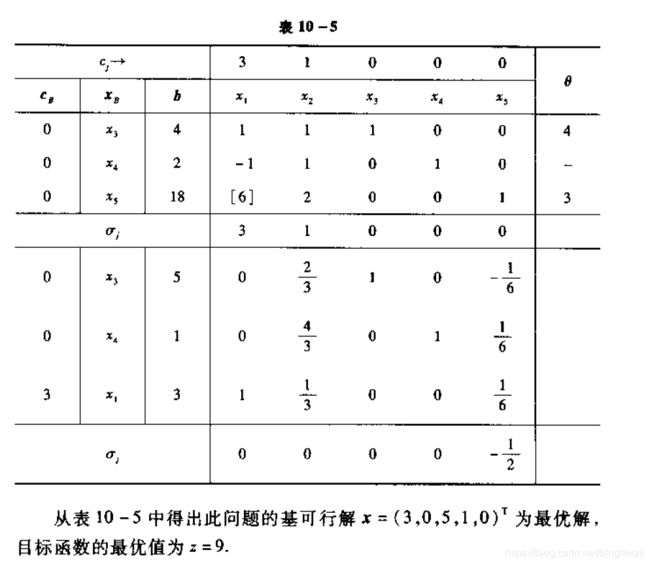
具体算法可以通过例题来加深，如课本所示：
课本上写的很简单，但是我算了很长时间才明白过来怎么迭代：
首先要写入系数矩阵A，b，以及原始的c，因为
，因此对应的c就为[3,1,0,0,0]。根据迭代的第一步，找到
=[0,0,4,2,18]，意思是当其他的元素都为0时，然后单位阵所对应的元素的解为.
第二步：找到
:其中:
在这里面，由于非基变量（上述的连接里面有提到）为 x3,x4,x5，基变量为x1,x2。所以第一个0是x4对应的c，第二个是x5对应的c，第三个是x6对应的c，在这里我弄了半天才懂。
同理算出
,
第三步：找到
,也就是说在这一步里面的
,因此判断3>0。所以这个解不是最优解。
第四步：对应的第k列也就是第一列，存在大于0的系数，因此存在最优解
第五步：
在这里面k=1,因此需要找到第一列中，大于0的元素的b/a值，其中
同理
也是，但是
不能求，因为对应的a小于0了。其中
最小，因此
为主元，第三行为主行（根据第五步判断出来的），第1列为主列（根据第三步判断出来的）
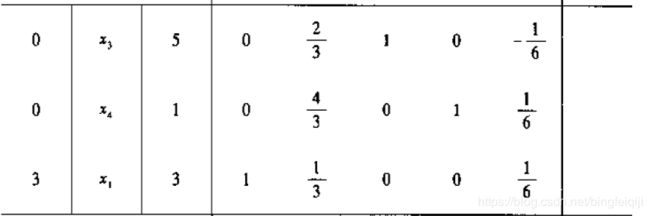
第六步：执行基变量变换,意思是将x1变为基变量，然后主行里面，系数为1对应的基变量，转化为非基变量。在这里，就是x5转化为非基变量。反正在这一步中，将原始的式子，通过消元，转化为以下形式。从上面的图上截取的：
但是在这里我算的b的数为[1,5,3]而不是[5,1,3] ，其他的都一样，也不知道是为什么，我算错了还是书上算错了，不太清楚。。先按书上的来吧。
在上面的表中，又能构建一个新的单纯型表。重复步骤一，将基变量设为0，解为
=[3,0,5,1,0].
第二步：
在这里面，每个式子的第一个0是x3对应的c，第二个0是x4对应的c，接下来的3是x1对应的c
第三步：
。结束判断，即。
最后的最后，带入目标函数