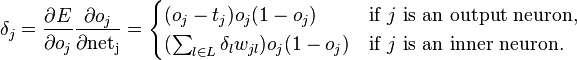对backpropagation的理解记录

记录对于wiki上的算法的理解过程。
链接：https://en.wikipedia.org/wiki/Backpropagation

参考：
https://en.wikipedia.org/wiki/Backpropagation
http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

1、概念
对于任何一个网络神经元节点j：
表示所有的上层节点到该j节点的输入，
表示经过了激活函数的输出，
总的表达式可以描述为：

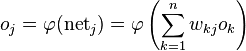
2、首先要确定cost函数（也有其他叫法）

where
E is the squared error,
t is the target output for a training sample, and
y is the actual output of the output neuron.

我们要根据这个形式来去最终推导权重更新的一般表达式。在中间计算过程中，我们可以简单的以E来代表就可以了，到最后的时候，才展开计算。

3、激活函数的选择

那么其导函数为：

为什么会需要导函数呢，在后面推导的时候需要用到。

4、最终目标函数

cost函数是计算得到的输出（o）与期望的输出（t）的差值，而期望输出（t）是输入样本里的内容，没什么好说的；计算得到的输出（o）的产生才是重点。
总的来说，o由激活函数对该节点的输入值进行计算得出，而该节点的输入值又等于与该节点相连的所有上层节点（假设是全连接）的输出乘于相应的连接权重的乘积的和，所以，我们可以知道o是与连接权重有关的函数计算出来的，因此cost函数（E）也是与连接权重有关的表达式，因此E对连接权重求导是有道理的。
分拆成3段的原因可以这样理解（当然从数学上是由链式规则得出，但是为什么这样拆的原因得说清楚）：E依赖于o，而o依赖于net，net才直接依赖于w。
这个是一般的表达式，并不特指哪层或哪个节点，因此，只要我们得到了这个偏导数的具体形式，我们就可以有公式来更新权重了。
（右边链式推导中，为什么不是下标为i呢？由上面的说明也知道，受 wij 影响的是连接线的下一层节点（即j节点），而不是上一层节点）

wiki通过对这个展开后的公式的每一项的计算推导，得出最终的表达式。
1）最后一项

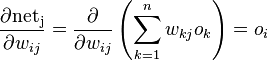
这个比较直接，直接计算就好了。
2）中间项

这个也好理解，同时也说了为何选择的激活函数需要可导的原因。

3）第一项
如果节点处于输出层，则这个好计算：

但是对于处于非输出层的，就不是那么明显了，也是这个推导的难处。
wiki上的两段话：
“
However, if j is in an arbitrary inner layer of the network, finding the derivative E with respect to oj is less obvious.

Considering E as a function of the inputs of all neurons L = {u, v, \dots, w} receiving input from neuron j,

and taking the total derivative with respect to oj , a recursive expression for the derivative is obtained:

”
如何理解，如何计算？
第一句话，是说考虑E是L层网元节点u,v,…w的输入的函数，这些节点接收了上一层节点j的输出作为输入（即 oj )。这样假设有没有道理呢？
有。上面说了，最终计算出来的y是经过了层层网元的输入输出的，当然其E也是与各层网元有关的。
既然有依据，那么对其后面的计算就是合理的。

那么看它的计算过程。
E的变量有 netu , netv ,… netw ，这些是复合变量，根据求导的公式 （忘了名字了，高等数学下册，回去查了再补），可以推出：

左边到中间项的计算。
再由中间演化到最右边项，是因为E对于net的关系不是直接的，而是经过了o的。
那 ∂netl∂oj 又是如何推导得到 wjl 呢？
这个其实跟：

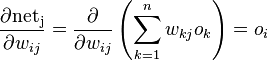
是一样的道理。

从这个公式：

我们看到了什么？
里面有：
∂E∂oj
有
∂E∂ol

而且前者依赖于后者，说明什么？为了计算前一层（靠近输入层）的这个偏导数，我们需要先计算出下一层的节点（与该上一层的节点有相连的）的偏导数，这就构成了一个递归的关系了：先计算出输出层节点的偏导数，然后逐层往前计算。

5、最终简化形式

其中：

到现在为止，这个公式已经出来了，那么更新权重的公式也可以得知了：
To update the weight wij using gradient descent, one must choose a learning rate, α . The change in weight, which is added to the old weight, is equal to the product of the learning rate and the gradient, multiplied by -1:

以上就是对wiki中backpropagation算法的理解记录过程。

对于感知机（就是单层的网络），其实就是这个的特殊情况，只有一层：输出层，这个 wij 的更新公式就成了delta rule（参考链接：
https://en.wikipedia.org/wiki/Delta_rule
）。

这里变成 hj 了，跟backpropagation里的 netj 是一个意思。