PCA的数学原理推导

PCA的数学推导

PCA（Principle Component Analysis）是一种可以将高维度数据降为低维度数据的机器学习算法。通过降维，可以有节省存储空间，数据可视化等优点。之前在Coursera上Andrew Ng的机器学习时了解到此算法，但是那个课只涉及了实现，并未阐述其背后的数学原理。之后在Coursera上又找到一门专门讲PCA数学原理的课程，才借此了解些许其中的数学原理，在此坐下记录，以便日后复习。

期望与方差

期望（Expectation）：简单来说，期望能够反映一组数据的平均值情况。其中一个定义为： E(X) = 1N∑Ni=1xi E ( X )   =   1 N ∑ i = 1 N x i 。由期望的定义不难得出以下性质：

E(X+a) = E(X)E(aX) = aE(x)(1)(2) (1) E ( X + a )   =   E ( X ) (2) E ( a X )   =   a E ( x )

方差（Variance）: 方差反映的是一组数据里各个数据点相对期望值的分散程度的总和。定义如下： Var(X) =  1N∑Ni=1(xi −E(X))2  V a r ( X )   =     1 N ∑ i = 1 N ( x i   − E ( X ) ) 2   。从方差的定义也不难推导出如下性质：

Var(X+a) = Var(X)Var(aX)=a2Var(X)(3)(4) (3) V a r ( X + a )   =   V a r ( X ) (4) V a r ( a X ) = a 2 V a r ( X )

协方差

协方差（Covariance）: 方差只是放映一个维度内的数据的分散程度，而协方差则用来表示不同纬度之间数据的相关性。
假设有两组数据X,Y，那他们的协方差定义为

Cov(X,Y) = 1N∑i=1N(xi −E(X))(yi−E(Y))=E[(X−E(X))(Y−E(Y))] C o v ( X , Y )   =   1 N ∑ i = 1 N ( x i   − E ( X ) ) ( y i − E ( Y ) ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ]

.
如果协方差是正数，代表两组数据正相关，简单来说就是一组数据若有变大趋势，另外一组也有变大的趋势。如果为负数，就是负相关。为零，则代表两组数据不相关。
对于多组数据，协方差通常表示为协方差矩阵（Covariance matrix）。假设两组数据X,Y, 那他们的协方差表示为

S =(cov(X,X)cov(Y,X)cov(X,Y)cov(Y,Y)) S   = ( c o v ( X , X ) c o v ( X , Y ) c o v ( Y , X ) c o v ( Y , Y ) )

协方差矩阵的维度D是数据的维度。例如有在实际应用中，数据会如下存储 X∈RN∗D X ∈ R N ∗ D , 这个说明数据按行存储，有N行，每个数据的维度D。在这种前提下，根据协方差矩阵定义和矩阵基本运算，协方差矩阵如下：

S = 1N(X−E(X))T(X−E(X))  S   =   1 N ( X − E ( X ) ) T ( X − E ( X ) )  

不难看出，协方差矩阵是对称矩阵（symmetric matrix）,且主对角线元素全都是大于等于0的。协方差矩阵具备一些良好的性质，可以为日后的计算带来很大的便利。关于实对称矩阵的半正定性质，一起其他性质，在另外一篇博客中记录。

内积

内积（inner product）: 不严格的来说，内积可以理解为在向量空间里定义的一种计算方法。具体的定义可见维基百科inner product。简单来说内积满足一下运算条件：
symmetric:

<x,y> = <y,x> < x , y >   =   < y , x >

bilinear:

<ax,y> = a<x,y><x+y,z> = <x,z>+<y,z> < a x , y >   =   a < x , y > < x + y , z >   =   < x , z > + < y , z >

positive definite:

<x,x> ⩾0, equality holds if only if x =0 < x , x >   ⩾ 0 ,   e q u a l i t y   h o l d s   i f   o n l y   i f   x   = 0

有了内积的定义，可以用来定义向量的长度，以及向量之间的夹角
向量的长度:

||x|| = <x,x>‾‾‾‾‾‾‾‾√ | | x | |   =   < x , x >

向量之间的角度:

cosθ=<x,y>||x||∗||y|| c o s θ = < x , y > | | x | | ∗ | | y | |

当向量之间角度为90度时，两个向量正交。可以看出向量的长度与向量之间的角度跟内积的具体定义有关系，我们通常所熟悉的点积（dot product）就是内积的一种。

投影矩阵

有了内积的定义，我们就可以继续定义什么是投影（projection）。

先从一维情况来看，当我们想在向量空间（vector space）U中找到一个向量p, 且希望||p-x||尽量小时，很明显当向量x-p垂直于向量p时，||p-x||最小。假设向量空间U的基（basis）为向量b。我们可以推导出一维时，投影矩阵。

∵p∈U, ∴p = λb, λ∈R由内积的正交的定义可得 <x−p,b> =0⇔<x−λb, b> = 0⇔<x,b>−λ<b,b> = 0⇔λ=<x,b>||b||2=xTb||b||2, 内积使用点积定义p = λb=xTb||b||2b∵xTb是标量，所以可以写成bTx∴p = bbT||b||2x  ∵ p ∈ U ,   ∴ p   =   λ b ,   λ ∈ R 由 内 积 的 正 交 的 定 义 可 得   < x − p , b >   = 0 ⇔< x − λ b ,   b >   =   0 ⇔< x , b > − λ < b , b >   =   0 ⇔ λ = < x , b > | | b | | 2 = x T b | | b | | 2 ,   内 积 使 用 点 积 定 义 p   =   λ b = x T b | | b | | 2 b ∵ x T b 是 标 量 ， 所 以 可 以 写 成 b T x ∴ p   =   b b T | | b | | 2 x  

关于更一般的投影矩阵推导，求参考 这里.

正交补和正交分解

正交补（orthogonal complement）和正交分解（orthogonal decomposition）的详细定义请参照维基百科。关键点是以下两点：

· If we look at an n-dimensional vector space V V and a k-dimensional subspace W∈V W ∈ V , then the orthogonal complement W⊥ W ⊥ is an (n−k)-dimensional subspace of V V and contains all vectors in V V that are orthogonal to every vector in W W .

这一点也比较好理解，一个向量空间V总能找到跟这个向量空间等价的一组标准正交基（orthonormal basis）,所以在V中的任何向量，都可以分解成这组标准正交基的线性组合。我们可以把这组标准正交基分为两组，其中一组就是另外一组的正交补，反之亦然，具体表现为第二个点。

· Every vector x∈V x ∈ V can be (uniquely) decomposed into
x = ∑ki=1λibi+∑n−kj=1ψjb⊥j, λi,ψj∈R  x   =   ∑ i = 1 k λ i b i + ∑ j = 1 n − k ψ j b j ⊥ ,   λ i , ψ j ∈ R   where b1,...bk b 1 , . . . b k is a basis of W W and b⊥1,...b⊥n−k b 1 ⊥ , . . . b n − k ⊥ is a basis of W⊥ W ⊥ .

PCA要解决的问题

假设我们一组数据 X={x1, x2, ... ,xn}, xi∈RD X = { x 1 ,   x 2 ,   . . .   , x n } ,   x i ∈ R D , 我们想要在更低的维度找到一组相似的数据来表示原有的数据。因为原数据的维度是 RD R D , 所以一下结论是可以推导出来的。

1. RD R D 内存在一组标准正交基（orthonormal basis 以后简称ONB），所以X可以被重新表示为： xn  = ∑Di=1Binbi x n     =   ∑ i = 1 D B i n b i
2. 由之前推导的一维投影公式可知， Bin=xTnbi B i n = x n T b i
3. 由正交分解可得， x = ∑ki=1βibi+∑n−kj=1ψjb⊥j, λi,ψj∈R  x   =   ∑ i = 1 k β i b i + ∑ j = 1 n − k ψ j b j ⊥ ,   λ i , ψ j ∈ R   ,我们可以把前半部分ONB看成主要的（Principle basis），后面的正补基看成次要的。PCA简而言之就是要找到一组主要的ONB（ b1,...bk b 1 , . . . b k ）和 相应的 B B (也叫坐标coordinates 或者code)，忽略后半部分。然后尽可能的保有原来数据的属性。所以经过PCA变换后的数据为： xn˜  = ∑ki=1Binbi x n ~     =   ∑ i = 1 k B i n b i
4. 损失函数定义如下： J = 1N∑Nn=1||xn−xn˜||2 J   =   1 N ∑ n = 1 N | | x n − x n ~ | | 2

计算投影的坐标

这部分以后下部分计算会涉及矩阵微分（matrix calculus）, 相关参考在这里。对 Bin B i n 的计算可以对J求偏导数得到，具体计算过程如下：
已知：

xn˜  = ∑j=1MBjnbjJ = 1N∑n=1N||xn−xn˜||2B={b1,...,bM},where b1,...,bM are orthonormal basis(1)(2)(3) (1) x n ~     =   ∑ j = 1 M B j n b j (2) J   =   1 N ∑ n = 1 N | | x n − x n ~ | | 2 (3) B = { b 1 , . . . , b M } , w h e r e   b 1 , . . . , b M   a r e   o r t h o n o r m a l   b a s i s

可得：

∂J∂xn˜=−2N(xn−xn˜)T∂xn˜∂Bjn=bj ∂ J ∂ x n ~ = − 2 N ( x n − x n ~ ) T ∂ x n ~ ∂ B j n = b j

∂J∂Bjn=∂J∂xn˜∗∂xn˜∂Bjn=−2N(xn−xn˜)Tbj=(1)−2N(xTnbj−(∑j=1MBjnbTj)bj)=(3)−2N(xTnbj − Bjn)且二阶导数∂2J∂B2jn=2N>0令一阶导数等于0，可得Bjn = xTnbj为最小值 (4) ∂ J ∂ B j n = ∂ J ∂ x n ~ ∗ ∂ x n ~ ∂ B j n = − 2 N ( x n − x n ~ ) T b j = (1) − 2 N ( x n T b j − ( ∑ j = 1 M B j n b j T ) b j ) = (3) − 2 N ( x n T b j   −   B j n ) 且 二 阶 导 数 ∂ 2 J ∂ B j n 2 = 2 N > 0 令 一 阶 导 数 等 于 0 ， 可 得 (4) B j n   =   x n T b j 为 最 小 值  

所以可以看出坐标就是原数据点在相应ONB上的投影。

求解目标维度空间的基

在计算之前，我们需要把损失函数重新改写下：

xn˜  = ∑j=1MBjnbj=∑j=1MxTnbjbj∵xTnbj是标量∴xTnbj =bTjxn, 且移到后面=∑j=1M(bjbTj)xn=BBTxn我们知道投影矩阵P = B(BTB)−1BT由公式（3）可知 BTB=I∴∑j=1M(bjbTj)就是principle subspace的投影矩阵 x n ~     =   ∑ j = 1 M B j n b j = ∑ j = 1 M x n T b j b j ∵ x n T b j 是 标 量 ∴ x n T b j   = b j T x n ,   且 移 到 后 面 = ∑ j = 1 M ( b j b j T ) x n = B B T x n 我 们 知 道 投 影 矩 阵 P   =   B ( B T B ) − 1 B T 由 公 式 （ 3 ） 可 知   B T B = I ∴ ∑ j = 1 M ( b j b j T ) 就 是 p r i n c i p l e   s u b s p a c e 的 投 影 矩 阵

由正交分解又可以得出：

xn = ∑j=1M(bjbTj)xn+∑j=M+1D(bjbTj)xn∴xn−xn˜= ∑j=M+1D(bjbTj)xn= ∑j=M+1D(bTjxn)bj(5) x n   =   ∑ j = 1 M ( b j b j T ) x n + ∑ j = M + 1 D ( b j b j T ) x n (5) ∴ x n − x n ~ =   ∑ j = M + 1 D ( b j b j T ) x n =   ∑ j = M + 1 D ( b j T x n ) b j

所以投影后形成的误差也可以看成原数据省略掉的正交补空间的投影。
重写损失函数J：

J = 1N∑n=1N||xn−xn˜||2=(5)1N∑n=1N||∑j=M+1D(bTjxn)bj||2=(3)1N∑n=1N∑j=M+1D(bTjxn)2=1N∑n=1N∑j=M+1DbTjxnxTnbj=∑j=M+1DbTj(1N∑n=1NxnxTn)bj=∑j=M+1DbTjSbj(6) J   =   1 N ∑ n = 1 N | | x n − x n ~ | | 2 = (5) 1 N ∑ n = 1 N | | ∑ j = M + 1 D ( b j T x n ) b j | | 2 = (3) 1 N ∑ n = 1 N ∑ j = M + 1 D ( b j T x n ) 2 = 1 N ∑ n = 1 N ∑ j = M + 1 D b j T x n x n T b j = ∑ j = M + 1 D b j T ( 1 N ∑ n = 1 N x n x n T ) b j (6) = ∑ j = M + 1 D b j T S b j

其中S就是协方差矩阵，因为我们假设数据已经被中心化（centralized）,也就是说 E(x)=0 E ( x ) = 0 .所以 S = 1N(XTX)  S   =   1 N ( X T X )   , 这个形式的协方差矩阵是因为我们之前约定 X ∈RN∗D X   ∈ R N ∗ D ,数据是行存储的。而在我们上面的推导中数据是列存储的， 所以协方差矩阵为 S=1N∑Nn=1xnxTn S = 1 N ∑ n = 1 N x n x n T ，所以形式上有些许不同。

在进一步计算之前需要复习下拉格朗日乘子法（Lagrange multiplier），拉格朗日乘子法是在限制条件下，求函数极值的方法。关于它的证明，这里给出一个链接。

先从一个简单例子出发，假设现在数据是二维的，并且ONB为 b1,b2 b 1 , b 2 ,现在要将数据投影在 b1 b 1 上，那么损失函数为：

J=bT2Sb2, with constraint bT2b2 = 1 J = b 2 T S b 2 ,   w i t h   c o n s t r a i n t   b 2 T b 2   =   1

使用拉格朗日乘子法, 其中计算要用到矩阵微分：

L(λ,b2) = bT2Sb2 + λ(1−bT2b2 )∂L∂λ=1−bT2b2  = 0∂L∂b2=2bT2S−2λbT2=0Sb2=λb2回代可得J=λbT2b2=λ (7) L ( λ , b 2 )   =   b 2 T S b 2   +   λ ( 1 − b 2 T b 2   ) ∂ L ∂ λ = 1 − b 2 T b 2     =   0 ∂ L ∂ b 2 = 2 b 2 T S − 2 λ b 2 T = 0 (7) S b 2 = λ b 2 回 代 可 得 J = λ b 2 T b 2 = λ  

可以看出 λ,b2 λ , b 2 是协方差矩阵S的特征值和特征向量，且当 b2 b 2 满足上述公式（7）时，可以取到极值，极值的个数就是特征向量的个数，极值就是各个特征值。所以利用这一点，当取到极值时，损失函数就等于 J=∑Dj=M+1λj J = ∑ j = M + 1 D λ j ，所以当我们要使损失函数最小时，我们就要找到最小的D-M个特征值，也就是我们所忽略的与M维子空间所正交的空间，他们要具有最小的特征值，损失才最小，换而言之，我们需要的M维子空间，他的ONB要具有前M个最大的特征值。

橘色箭头代表协方差矩阵的两个特征向量，向量的长度与特征值的长度成正比，很显然，当我们把数据投影到较长的橘色向量上的时候，我们能保留更多的信息。

高纬度下PCA使用

当数据 X∈RN∗D X ∈ R N ∗ D 的维度远远大于数据量的时候(D >> N)，计算协方差矩阵 S = 1N(XTX)  S   =   1 N ( X T X )   会比较耗时，所以我们通过计算 1N(XXT)  1 N ( X X T )   和其他一些步骤来获得相同的效果，证明如下：

由公式（7）知Sb=1NXTXb=λb左乘X⇔(1NXXT)Xb = λ(Xb)令Xb = c左乘XT⇔(1NXTX)XTc=λXTc 由 公 式 （ 7 ） 知 S b = 1 N X T X b = λ b 左 乘 X ⇔ ( 1 N X X T ) X b   =   λ ( X b ) 令 X b   =   c 左 乘 X T ⇔ ( 1 N X T X ) X T c = λ X T c

由以上推导我们知道 1N(XXT)  1 N ( X X T )   跟协方差矩阵有同样的特征值，当计算完 1N(XXT)  1 N ( X X T )   的特征向量 c c 后，右乘 XT X T 即可得到协方差矩阵的特征向量。

PCA步骤

1. 首先对数据进行中心化处理，这要做的目的其一是免去一些数值问题（numerical problem）。
   

   x=x−E(x) x = x − E ( x )

2. 在对上述数据除以标准差，这样做就可以使各维度数据忽略个维度的单位（make it unit free），但是保留完成的相关性(maintain all correlation)。如果不做此操作，则数据之间的相关性可能会表现有误。
   
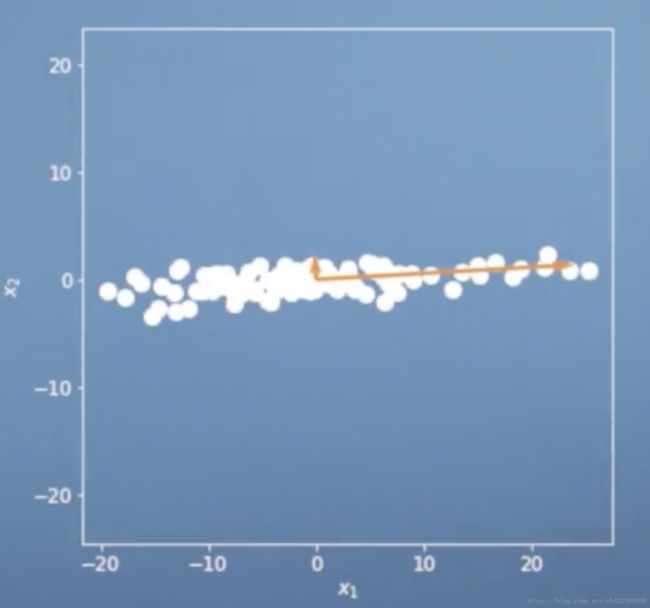
   如上图所示，例如当一位维度的单位是米，另外一个维度的单位毫米的时候，数据分布如图所示，如果这时候使用PCA，很明显，更倾向于是分散更开的维度投影（投向毫米这个维度）。在除以标准差之后，所有维度的方差都为1，这就就可以保持维度之间的相关性而忽略单位。
   
   除以标准差（standard deviation）之后，数据的分布如图所示。这是，协方差矩阵的特征值和特征向量也发生变化，这时更能体现出正确的相关性。

3. 计算协方差矩阵的特征向量和特征值，选出前M个最大的特征向量和特征值，特征向量排列的矩阵 BM={b1, b2, ..., bm} B M = { b 1 ,   b 2 ,   . . . ,   b m } ，根据前面的推理，投影后，在由 BM B M 所生成的线性空间中的坐标（linear space spanned by BM B M ）为 z=BTM∗x, BTM∈Rm∗d, x∈Rd∗1 z = B M T ∗ x ,   B M T ∈ R m ∗ d ,   x ∈ R d ∗ 1 。若在原线性空间中表示这些点则为 x̃ =BM∗z=BMBTMx x ~ = B M ∗ z = B M B M T x ，这一步在Coursera上的Andrew NG教的ML中也叫数据点重建（reconstruction of the original data）。

结语

以上就是对Coursera上的PCA数学原理的总结，其中的数学推理，个人感觉有些地方日后还需要更加深入的理解，例如多元复杂函数求极值的问题。如果能通过实际项目来做一遍的话，应该会有更好的理解。如果文中有任何问题，或者各位读者有任何疑问，请留言，欢迎大家一起讨论问题。

补充

今日重温了下Coursera上Andrew NG的机器学习中的PCA一章，所介绍的算法中他用了SVD而不是特征值分解，其实这两个算法给出的结果是一模一样的，因为这两个算法的输入都是协方差矩阵，协方差矩阵是对称，且半正定的（positive semi-definite）。用SVD的原因Andrew解释说是SVD更加稳定（numerical stable）。

关于如何选择多少个主成分（principle component）：
Coursera上ML的视频在此。

直觉上来说，这也是比较合理的，因为之前所讲的，我们需要根据特征值的大小来选择需要投影的方向，因为有些方向上的特征值很小，所以可以忽略。