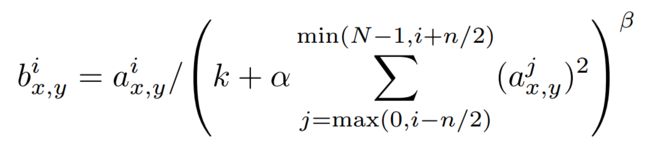LRN (Local Response Normalization,即局部响应归一化层)
LRN (Local Response Normalization,即局部响应归一化层)
(一)先看看归一化吧
什么是归一化?
归一化化是归纳统一样本的统计分布性。就是要把你需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内。
为什么要归一化,归一化目的是什么?
(1)为了后面数据处理的方便,归一化的确可以避免一些不必要的数值问题。
(2)为了程序运行时收敛加快。 下面图解。
(3)同一量纲。样本数据的评价标准不一样,需要对其量纲化,统一评价标准。这算是应用层面的需求。
(4)避免神经元饱和。啥意思?就是当神经元的激活在接近0或者1时会饱和,在这些区域,梯度几乎为0,这样,在反向传播过程中,局部梯度就会接近0,这会有效地“杀死”梯度。
(5)保证输出数据中数值小的不被吞食。
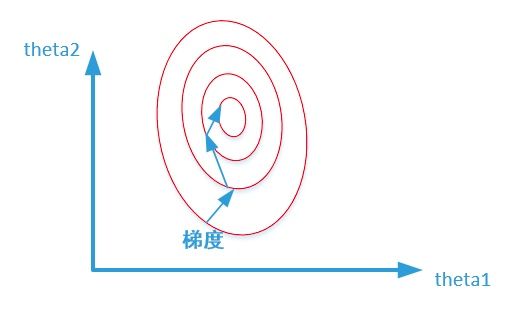
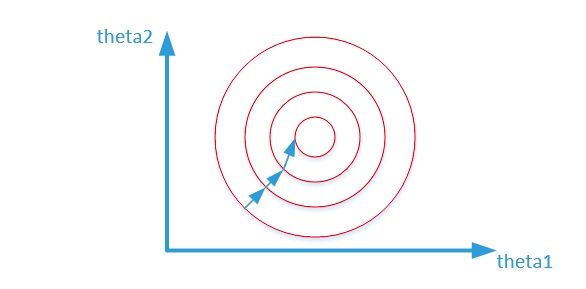
两张图代表数据是否均一化的最优解寻解过程(圆圈可以理解为等高线),下面2张图来自知乎。
未归一化:
归一化之后:
再来个3D的效果图说明下不归一化的情形:
例子:
假设 w1 的范围在 [-10,10],而w2的范围在[-100,100],梯度每次都前进1单位,那么在w1方向上每次相当于前进了 1/20,而在w2上只相当于 1/200!某种意义上来说,在w2上前进的步长更小一些,而w1在搜索过程中会比w2“走”得更快。
这样会导致,在搜索过程中更偏向于w1的方向。走出了“L”形状,或者成为“之”字形。
归一化有哪些方法? (常用1、2)
1、min-max标准化(Min-Max Normalization)
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 – 1]之间。转换函数如下:
y=(x−min)/(max−min)
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
2、Z-score标准化方法
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
y=(x−μ)/σ
其中 μ为所有样本数据的均值,σ为所有样本数据的标准差。
3、Z-scores 简单化
模型如下:
y=1/(1+x)
x越大证明y 越小,这样就可以把很大的数规范在[0-1]之间了。
4、对数函数转换
y=lg(x),其中lg即以10为底的对数
5、反余切函数转换
y=atan(x)*2/PI
我×,跑题了,本文应该讲LRN的。算了,不删了,继续讲LRN吧。
(二)LRN (Local Response Normalization,即局部响应归一化层)
LRN即对 一个输入的局部区域进行归一化,应用成功的实例: AlexNet 或GoogLenet。其实本质上是一样的,神经网络即时发现潜在的“数据分布规律”的工具,所以要求训练数据和测试数据具有相同的数据分布,如果不一样,那么发现的规律就没用,即网络的泛化能力不行。呵呵。
在训练大量的练数据过程中,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在
每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
即,通过归一化,我们就可以在一个标准下找“规律”了。
LRN开始出现在Caffe里面的,
Caffe中具体实现在CAFFE_ROOT/src/caffe/layers/lrn_layer.cpp和同一目录下lrn_layer.cu中,使用只需要做如下配置:
layers
{
name: "norm1"
type: LRN
bottom: "pool1"
top: "norm1"
lrn_param {
local_size: 5
alpha: 0.0001
beta: 0.75
}
}
来看下它的公式吧:
norm_region: 选择对相邻通道间归一化还是通道内空间区域归一化,默认为ACROSS_CHANNELS,即通道间归一化;
有两个选择:
(1)ACROSS_CHANNELS表示在相邻的通道间求和归一化,表示局部区域沿临近通道延伸,局部区域块形状为local_size * 1 * 1。
(2)WITHIN_CHANNEL表示在一个通道内部特定的区域内进行求和归一化。局部区域形状为1 * local_size * local_size。
local_size:两种表示
(1)通道间归一化时,表示求和的通道数;
(2)通道内归一化时,表示求和区间的边长;默认值为5;
alpha:缩放因子(详细见后面),默认值为1;
beta:指数项(详细见后面), 默认值为5;
n:局部尺寸大小local_size,以当前输入值为中心的区域内计算加和,有时补零。
注:Caffe升级后,公式里的1变成了k,主要意思没变。
(三)Tensorflow中的LRN
tensorflow中的LRN,公式如下:
官方说明如下:
sqr_sum[a, b, c, d] = sum(input[a, b, c, d - depth_radius : d + depth_radius + 1] ** 2)
output = input / (bias + alpha * sqr_sum) ** beta
这里关于求batch的sqr_sum还是比较复杂了,主要意思是在一个3维空间范围内,取所有像素的点,求平方和,直接套用吧,以alexnet的论文为例,输入暂且定为 [batch_size, 224, 224, 96],这里224×224是图片的大小,经过第一次卷积再经过ReLU,就是LRN函数的输入。
运行Tensorflow测试代码:
import numpy as np
import tensorflow as tf
a = np.ones([2, 2, 3, 3])
#sqr_sum[a, b, c, d] = sum(input[a, b, c, d - depth_radius : d + depth_radius + 1] ** 2)
#output = input / (bias + alpha * sqr_sum) ** beta
b = tf.nn.local_response_normalization(a, 1, 0, 1, 1)
print("Initial array:")
print(a)
sess = tf.Session()
print("\nOutput after normalization")
print(sess.run(b))
这里输入a,可以理解为一个4维张量,形象点就是 2*2 矩阵,该矩阵每个元素又是 3*3的矩阵。所有的初始值都为1。运行结果如下:
好像有点啰嗦了,其实,直接套用就好啦,结束。