0x07算法设计与分析复习（二）：算法设计策略-动态规划法2

参考书籍：算法设计与分析——C++语言描述（第二版）

算法设计策略-动态规划法

资源分配问题

资源分配问题

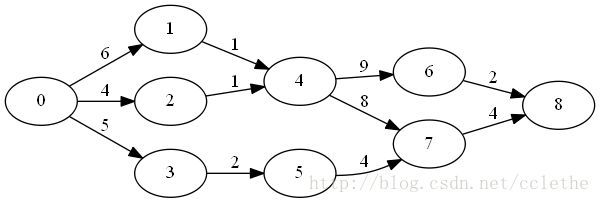
将n个资源分配给r个项目，已知如果把j个资源分配各第i个项目，可以收益 N(i,j),0≤j≤n,1≤i≤r ，求总收益最大的资源分配方案。

这一问题可以用一个多段图来描述，多段图共分为 r+1 阶段，第1阶段是开始阶段，只包含一个初始状态；最后一个阶段即第 r+1 阶段是结束阶段，表示整个分配完成，因此也只有一个结束状态t；除此以外的 r−1 个中间阶段，每个阶段包含 n+1 个状态。

多段图中每个状态 V(i,j) 代表已将j个资源分配给前 i−1 项目，其中 s=V(1,0),t=V(r+1,n) 。图中的边都具有 <V(i,j),V(i+1,k)>(0≤j≤k≤n,1≤i≤r) 的形式，代表为第i个项目分配了 k−j 个资源，边上的权值 N(i,k−j) 是本次分配的收益。图中最后两个阶段间的边 <V(r,j),V(r+1,n) 的权值取 max0≤p≤n−j{N(r,p)} 。虽然一般来说，分配的资源数目越多应有较多的收益，但并非完全如此。

从源点s到任意结点 V(i,j) 的一条路径代表一种子资源分配方案。从s到汇点t的一条路径代表一种可能的资源分配方案，其路径长度是在该方案下的总收益值。从s到t的最长路径对应于最有资源分配方案。

关键路径问题

关键路径问题

关键路径问题是求解一个带权有向无环图中两个结点间的最长路径问题。关键路径问题是一个AOE网络问题。

AOE（activity on edge）网络是一个带权有向图 G=(V,E) ，它以结点代表事件（event），有向边代表活动（activity），有向边的权表示一项活动的持续时间（duration）。每个结点所代表的事件是指它的入边代表的活动均已完成，由他的出边所代表的活动可以开始这样一个事实。设 w(i,j) 是边 <i,j> 的权值，它表示完成活动 ak 所需的时间。

利用AOE网络可以进行工程的安排。例如，研究完成整个工程至少需要多少时间，为缩短工期应该加快哪些活动的速度，以及决定哪些活动是影响工程进度的关键等。由于整个工程只有一个开始状态和一个完成状态，故正常情况下（无回路），AOE网中只有一个入度为零的结点，称为源点，以及一个出度为零的结点，称为汇点。

关键路径法是进行工程安排的一种方法。完成工程所需的最短时间是AOE网中从开始结点到完成结点的最长路径的长度。这条路径称为关键路径，分析关键路径的目的在于找到关键活动。所谓关键活动就是指对整个工程的最短工期有影响的活动，即如果它不能如期完成就会影响整个工程的进度。

最短完成时间：是从源点到汇点的最长路径长度。

关键路径：从源点到汇点的最长路径。

关键活动：关键路径上的活动。对整个工程的最短完成时间有影响的活动，即如它不能按期完成就会影响整个工程的进度。

找关键活动的目的：
+ 重视关键活动；

对关键活动投入较多的人力和物力，确保工程按期完成。

• 缩短整个工期。

  关键活动对缩短整个工期起着至关重要的作用；非关键活动对缩短整个工期不起作用。

最优子结构和重叠子问题

最优子结构和重叠子问题是动态规划法求解的基本要素。关键路径问题可以用动态规划算法求解，正因为它具有最优子结构和重叠子问题特性。

容易证明，对于关键路径问题的最优解具有最优子结构特征。关键路径问题的最优解是从源点s到汇点t的最长路径，设为 (s,⋯,u,t) ，其中包含了从源点s到结点u的子路径 (s,⋯,u) 。如果路径 (s,⋯,u,t) 是从源点s到汇点t的最长路径，必定要求子路径 (s,⋯,u) 是从源点s到结点u的最长路径，否则路径 (s,⋯,u,t) 就不是最长路径。这就是该问题的最优子结构特性。

求关键路径的动态规划算法

• 事件i可能的最早发生时间 earliest(i) ：是指从开始结点s到结点i的最长路径的长度。
• 事件i允许的最迟发生时间 latest(i) ：是指在不影响工期的条件下，事件i允许的最晚发生时间，它等于 earliest(n−1) 减去从结点i到结点n-1的最长路径的长度。
• 关键活动：若 latest(i)−earliest(i)=w(i,j) ，则边 <i,j> 代表的活动是关键活动。对于关键活动组成的关键路径上的每个点i，都有 latest(i)=earliest(i) 。

初始时， earliest(s)=0 。 earliest(t) 就是从源点s到汇点t的关键路径长度。求关键路径可用如下定义的向后递推式计算：

⎧⎩⎨earliest(0)=0earliest(j)=maxi∈P(j){earliest(i)+w(i,j)}  0<j<n

式中， P(j) 是所有以j为头的边 <i,j> 的尾结点i的集合， w(i,j) 是边 <i,j> 的权。上式表示，只要从s到i的最长路径 earliest(i) 已经求得，就可以计算 earliest(j) 。与多段图类似，只需对结点按图G的某种拓扑次序编号，就可顺利地从结点0开始，按结点编号依次计算每个 earliest(i) 的值，最终求得的 earliest(n−1) 就是最优解值。

所谓某个事件允许的最迟发生时间是在保证最短工期的前提下计算的。以下是计算事件允许的最迟发生时间的递推式：

⎧⎩⎨latest(n−1)=earliest(n−1)latest(i)=minj∈S(i){latest(j)−w(i,j)}  0≤i<n−1

计算从汇点 latest(n−1)=earliest(n−1) 开始，从后向前按照一定次序递推计算其他结点的 latest(i) 值。其中， S(i) 是所有以i为尾的边 <i,j> 的头结点j的集合。这一公式要求计算某个 latest(i) 的值时，所有的 latest(j)，j∈S(i) 已经求得。这只需按逆拓扑次序进行递推计算即可。

关键路径问题同样存在重叠子问题，关键路径算法将子问题的最优解的值保存在earliest数组中。

关键路径算法

求解关键路径的基本步骤：
1. 对有向图G进行拓扑排序，确认是否为有向无环图；
2. 按拓扑次序计算 earliest[i],0≤i<n−1 ；
3. 按逆拓扑次序计算 latest[i],0≤i<n−1 ；
4. 对每一条边 <i,j> ，计算 latest[i]−earliest[i] ，并检查 latest[i]−earliest[i] 是否等于 w[i][j] ， w[i][j] 是边 <i,j> 的权，从而确定关键活动。

每对结点间的最短路径

问题描述

设 G=(V,E) 是一个有n个结点的带权有向图， w(i,j) 是权函数，

w(i,j)=⎧⎩⎨⎪⎪边<i,j>上的权值0∞如果如果如果<i,j>∈Ei=j<i,j>∉E

每对结点间的最短路径问题是指求图中任意一对结点i和j之间的最短路径。

迪杰斯特拉算法可以求解单源最短路径问题，其时间复杂度为 O(n2) 。为了求解任意一对结点间的最短路径，可以分别以图中每个结点为源点，n次调用迪杰斯特拉算法进行计算，其时间复杂度为 O(n2) 。但迪杰斯特拉算法要求图中的边带非负权值。

对于带权有向图的最短路径问题可以允许有向图包含负边，但不允许有路径长度为负值的回路。

弗洛伊德（Floyd）算法是一种动态规划算法，它求带权有向图 G=(V,E) 中所有结点之间的最短路径。

动态规划法求解

最优子结构

设图 G=(V,E) 是带权有向图， δ(i,j) 是从结点i到结点j的最短路径长度，k是这条路径上的一个结点， δ(i,k) 和 δ(k,j) 分别是从i到k和从k到j的最短路径长度，则必有 δ(i,j)=δ(i,k)+δ(k,j) 。若不然，则 δ(i,j) 代表的路径就不是最短路径。这表明每对结点之间的最短路径问题的最优解具有最优子结构特性。

最优解的递推关系

设 dk[i][j] 是从结点i到结点j的路径上，只允许包含结点编号不大于k的结点时，所有可能路径中的最短路径长度。因为图中不存在编号比n-1更大的编号，所以 δ(i,j)=dn−1[i][j] 。因为最优子结构特性，有

dn−1[i][j]=min{dn−2[i][j],dn−2[i][n−1]+dn−2[n−1][j]}

则 dn−1[i][j] 必定是 dn−2[i][j] 和 dn−2[i][n−1]+dn−2[n−1][j] 这两条路径的较短者。

一般有， dk[i][j]=min{dk−1[i][j],dk−1[i][k]+dk−1[k][j]}

式中， dk−1[i][j] 、 dk−1[i][k] 和 dk−1[k][j] 分别是相应两结点间的路径上只包含结点号不大于 k-1的路径中的最短者。若不然， dk[i][j] 也不可能是从结点i到结点j的路径上，只允许包含结点编号不大于k的结点时的所有路径中的最短者。

以上的讨论归结为以下递推式：

d−1[i][j]={w(i,j)∞若<i,j>∈E若<i,j>∉Edk[i][j]=min{dk−1[i][j], dk−1[i][k]+dk−1[k][j]}, 1≤k≤n−1

式中， d−1[i][j]​ 代表从i到j的路径上不包含任意其他结点时的长度。

重叠子问题

从递推式可以看出，为了计算 dk[i][j] ，必须计先算 dk−1[i][j] 、 dk−1[i][k] 和 dk−1[k][j] ， dk−1 的元素被多个 dk 的元素的计算共享。

弗洛伊德算法

弗洛伊德算法是一种动态规划算法，它采用自底向上的方式对计算每个结点间的最短路径。设有向图存储在邻接矩阵 a 中，初始时 d[i][j]=a[i][j] 。二位数组d用于保存各条最短路径的长度。在算法的第 k(k=0,1,⋯,n−1) 步上应做出决策：从i到j的最短路径上是否包含结点k。

弗洛伊德算法使用一个二维数组path来记录相应的最短路径， path[i][j] 给出从结点i到j的最短路径上结点j的前一个结点，以此来计算最优解对应的路径。

//弗洛伊德算法
template<class T>
  void MGraph::Floyd(T**& d,int**& path)
  {
    int i,j,k;
    d=new T*[n];
    path=new int *[n];
    for(i=0;inew T[n];
      path[i]=new int[n];
      //初始化
      for(j=0;jif(i!=j && w[i][j]else 
          path[i][j]=-1;
      }
    }
    //考察结点
    for(k=0;kfor(i=0;ifor(j=0;jif(d[i][k]+d[k][j]

弗洛伊德算法的时间复杂度为 O(n3) ，其正确性容易用归纳法证明（动态规划算法都可以用类似算法证明）。

定理：弗洛伊德算法得到的d[i][j]， 0≤i,j≤n−1 是从i到j的最短路径。