树状数组升级版（二维树状数组）

我在前面已经介绍过了树状数组的各种操作，但是你会轻易的发现前面我们介绍的树状数组都是一维的，那既然一维可以，那么会不会有二维的树状数组呢？
答案是肯定的。
那么我今天就来教大家如何实现二维的树状数组。
今天我介绍基本的功能：

1. 对二维数组内某一点加上一个值
2. 求一原点为一个端点的子矩阵和
3. 求以二维数组中的两个点为端点的子矩阵和

我们先来讲讲怎么去表示。（分析字太多了，以下的分析采用南宫逸辰的分析）
数组A[][]的树状数组定义为：

C[x][y] = ∑ a[i][j], 其中，
x-lowbit(x) + 1 <= i <= x,
y-lowbit(y) + 1 <= j <= y.

例：举个例子来看看C[][]的组成。
设原始二维数组为：
　A[][]={{a11,a12,a13,a14,a15,a16,a17,a18,a19},
{a21,a22,a23,a24,a25,a26,a27,a28,a29},
{a31,a32,a33,a34,a35,a36,a37,a38,a39}，
{a41,a42,a43,a44,a45,a46,a47,a48,a49}};
那么它对应的二维树状数组C[][]呢？

记:
B[1]={a11,a11+a12,a13,a11+a12+a13+a14,a15,a15+a16,…} 这是第一行的一维树状数组
B[2]={a21,a21+a22,a23,a21+a22+a23+a24,a25,a25+a26,…} 这是第二行的一维树状数组
B[3]={a31,a31+a32,a33,a31+a32+a33+a34,a35,a35+a36,…} 这是第三行的一维树状数组
B[4]={a41,a41+a42,a43,a41+a42+a43+a44,a45,a45+a46,…} 这是第四行的一维树状数组
那么：
C[1][1]=a11,C[1][2]=a11+a12,C[1][3]=a13,C[1][4]=a11+a12+a13+a14,c[1][5]=a15,C[1][6]=a15+a16,…
这是A[][]第一行的一维树状数组

C[2][1]=a11+a21,C[2][2]=a11+a12+a21+a22,C[2][3]=a13+a23,C[2][4]=a11+a12+a13+a14+a21+a22+a23+a24,
C[2][5]=a15+a25,C[2][6]=a15+a16+a25+a26,…
这是A[][]数组第一行与第二行相加后的树状数组

C[3][1]=a31,C[3][2]=a31+a32,C[3][3]=a33,C[3][4]=a31+a32+a33+a34,C[3][5]=a35,C[3][6]=a35+a36,…
这是A[][]第三行的一维树状数组

C[4][1]=a11+a21+a31+a41,C[4][2]=a11+a12+a21+a22+a31+a32+a41+a42,C[4][3]=a13+a23+a33+a43,…
这是A[][]数组第一行+第二行+第三行+第四行后的树状数组

好，南宫逸辰分析结束。
我简单总结一下，说白了，就是每一行都是一个树状数组，
以行为元素，整个列也是一个树状数组。（这句话请记住，这个思想会贯穿始终）
既然如此，我相信代码也很快就出来了，接下来我就来给出代码，并进行简单的解释。

单点修改

void add(int x,int y,int p){  
    while(x<=n){
        for(int i=y;i<=m;i+=lowbit(i)){
            C[x][i]+=p;
        } 
        x+=lowbit(x);
    }  
}  

这个根据我刚刚说的两个树状数组（那句贯穿始终的话），就很容易理解了。
我们外围循环枚举每一行，内循环在行内进行一维树状数组的单点修改，从而实现二维树状数组的单点修改。

以原点为一个端点的子矩阵和

int sum(int x,int y){  
    int result = 0;  
    while(x>0){
        for(int i=y;i>0;i-=lowbit(i)){
            result+=C[x][i];
        }
        x-=lowbit(x);
    }  
    return result;  
}  

还是那句贯穿始终的话，外围枚举行，内围则是一维树状数组前几项和。这样就能完成我们的任务了。

以任意两点为左上和右下两个端点的子矩阵和

int ask(int x1,int y1,int x2,int y2){
    return sum(x2,y2)+sum(x1-1,y1-1)-sum(x2,y1-1)-sum(x1-1,y2);
}

和以为树状数组一样，我们依然借助sum去求。
但是，我们看到，这个公式似乎很长，别急，别晕，听我解释一边即可明白。
首先声明，我们保证x2>=x1,y2>=y1
下面让我们先来看一个图：

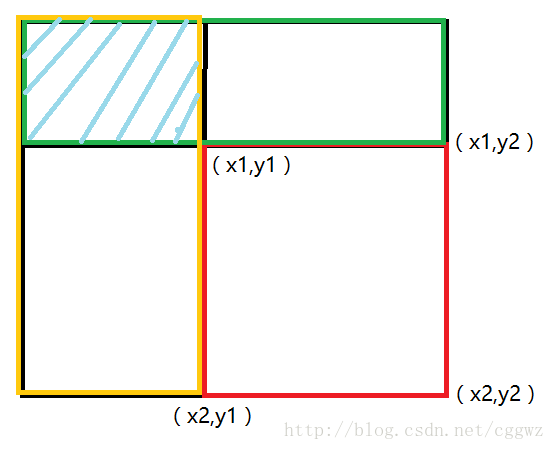
红色的矩形是我们要求的。
我们这里为了和计算机里二维数组的保持一致，我们把x坐标视为纵坐标。（感谢qie_wei指正我的错误）
首先sum(x2,y2)很显然是整个大矩形，
sum(x1-1,y2)和sum(x2,y1-1)则是绿色和黄色的两个矩阵（不含红色边），很明显这是我们不要的，所以我们用大的矩阵减去这两个小矩阵。
但是，减完以后我们会发现蓝色阴影部分的矩阵被减了两次，很明显减多了，所以我们还需要加上sum(x1-1,y1-1)
这样就成了我给的公式。

总结

不是很难，但改进的很巧妙。
注意复习，随后我会发一道练习题。