图像生成：GAN

简介

GAN，即生成对抗模型，是图像生成领域内的一种重要方法，它在2014年由Goodfellow提出，它的论文是《Generative Adversarial Networks》，GAN是在训练两个相互对抗的网络，一个生成器(Generator)和一个判别器(Descriminator)。当训练达到平衡时，对于一个输入噪声$z$。$G(z)$就是最后生成出来的图像。

GAN原理

GAN结构

GAN的结构非常简单，就像上图这样，它有一个生成器G（Generator）和一个判别器D（Discriminator）：生成器的输入是一组随机的变量，输出是生成的图；判别器负责对生成的图进行打分，输出是一个0-1之间的置信度。
对于生成器G，希望生成的图像$G(z)$无限逼近于真实图像，而对于判别器D，希望无论生成的图像$G(z)$有多真实，判别器总是能把他和真实的图像区分开，所以说GAN是一个G和D博弈的过程。
这个过程在GAN训练时体现的更为明显，就像两个人下棋一样，一个人走棋时，另一个人要等对方走完才能走棋，GAN的训练也是这样，生成器G和判别器D的优化是分开的，并相互交替迭代。

上面这张图中，训练开始时，黑线、绿线和蓝线分别代表真实样本分布、生成器生成的样本分布以及判别模型。

• 图(a)是训练前最初的状态;
• 图(b)是固定生成器G，训练判别器D的结果，使判别器可以区分出生生成样本分布和真实样本分布；
• 图( c)是固定上一步的判别器D，训练生成器G的结果，使生成的样本分布更接近真实样本分布，骗过当前的判别器；
• 图(d)是经过多次的迭代，生成器和判别器达到平衡，生产样本无限接近真实样本分布，判别器无法区分出来。

在实际的训练中，生成器G和判别器D的优化不是逐次交替的，而是每训练k次的判别器D后，训练一次生成器G，这样能保证G的变化足够慢，使总是能D保持在其最佳解附近。

GAN损失函数

虽然GAN的优化是交替进行的，但是损失函数可以表达为一个。GAN的损失函数：
$$\underset{G}{\min }\underset{D}{\max }V(G,D)={\mathbb{E}}_{x\sim p_{data}(x))}[logD(x)]+{\mathbb{E}}_{z\sim p_z(z))}[log(1-(D(G(z)))]$$
其中$p_{data}$代表真实的样本分布，$p_z$代表生成的样本分布，优化生成器G时，固定住当前的判别器D。判别器D的输出结果在0-1之间，当输出为1时认为是真实样本。生成器G优化的目的是骗过判别器D，即$D(G(z))$趋近于1，$1-D(G(z))$趋近于0，而$logD(x)$的最大值也仅仅是0。所以优化生成器是最小化$V(G,D)$：
$$\underset{G}{\min }V(G,D)={\mathbb{E}}_{x\sim p_{data}(x))}[logD(x)]+{\mathbb{E}}_{z\sim p_z(z))}[log(1-(D(G(z)))]$$
另一种情况是，固定生成器G，优化判别器D。判别器D优化的目的是无论生成的样本多么接近真实样本，都能判别出来。所以即$D(G(z))$趋近于0，$1-D(G(z))$趋近于1。所以优化判别器是最大化$V(G,D)$：
$$\underset{D}{\max }V(G,D)={\mathbb{E}}_{x\sim p_{data}(x))}[logD(x)]+{\mathbb{E}}_{z\sim p_z(z))}[log(1-(D(G(z)))]$$

GAN的判别器损失函数其实是一个二值交叉熵，因为判别器D最后输出一个回归值，压缩到0-1后，用于真假的二分类，但是它和二值交叉熵的写法有些区别，下面是二值交叉熵损失：
$$L(p,t)=-[plog(t)+(1-p)log(1-t)]$$
GAN的损失没有负号，这是因为二值交叉熵$L(p,t)$默认了损失最小为优，而GAN的判别器损失，目的是$\underset{D}{\max }V(G,D)$。

GAN训练过程

实际的损失计算过程和上述公式有些差异，主要在于优化生成器的时候，${\mathbb{E}}_{x\sim p_{data}(x))}[logD(x)]$不参与计算。对于判别器，虽然它的输出是0-1之间的一个数，但是它的目的其实是二分类，因为一个被压缩到0-1之间的结果相当于做二分类logist。
同时我们知道了分别优化生成器和判别器时，判别器的期望值，即最大化的判别器损失和最小化的生成器损失的区别在于判别器的期望值不同。所以这个损失可以用二值交叉熵来做，下面是一个PyTorch实现的例子：
假设我们定义好了生成器和判别器模型，分别叫做Generator和Discriminator，分别构建它们的optimizer。

#二值交叉熵损失
criterion = nn.BCELoss()
#生成器optimizer
g_optimizer = torch.optim.Adam(Generator.parameters(), lr=0.0002)
#判别器optimizer
d_optimizer = torch.optim.Adam(Discriminator.parameters(), lr=0.0002)
 # 定义真实label为1 可以假设batch_size=1
real_label = Variable(torch.ones(batch_size)).cuda() 
# 定义假的label为0 可以假设batch_size=1
fake_label = Variable(torch.zeros(batch_size)).cuda()  

训练生成器G：

# 生成随机噪声z
z = Variable(torch.randn(batch_size, z_dimension)).cuda()  
# 生成器通过z生成假的图片fake_img 
fake_img = Generator(z)  
# fake_img得到判别结果output 
output = Discriminator(fake_img) 
# output的期望值为1，即real_label，计算生成器损失
# 只有一个损失
g_loss = criterion(output, real_label)   
#优化Generator
g_optimizer.zero_grad() 
g_loss.backward()  
g_optimizer.step() 

训练判别器D：

# 将真实的图片放入判别器中，得到real_out 
real_out = D(real_img)  
# real_out 的期望值为1，即real_label，计算判别器损失1 
d_loss_real = criterion(real_out, real_label)  
# 生成随机噪声z
z = Variable(torch.randn(batch_size, z_dimension)).cuda()  
# 生成器通过z生成假的图片fake_img 
fake_img = G(z) 
# fake_img得到判别结果fake_out 
fake_out = D(fake_img) 
# fake_out 的期望值为0，即fake_label，计算生成器损失
d_loss_fake = criterion(fake_out, fake_label)  
# 将真假图片的loss加起来
# 有两个损失
d_loss = d_loss_real + d_loss_fake  
#优化Discriminator
d_optimizer.zero_grad()  
d_loss.backward()  
d_optimizer.step()  

GAN生成效果

GAN在MNIST，TFD和CIFAR-10三个数据集上测试了生成效果，分别是MNIST为图a)，TFD为图b)，CIFAR-10为图c)和图d)。
当然现在来看的话，这个结果照比BigGAN和styleGAN这样的模型来说，差了很远，但是在当时已经是相当惊艳了。

GAN、VAE和CNN

最后说明一下GAN，VAE和CNN的关系，GAN和VAE、CNN是相互独立的，没有包含或被包含的关系。它们的关系应该是这样：

其中的交集是三种方法结合使用的部分。

AE和VAE

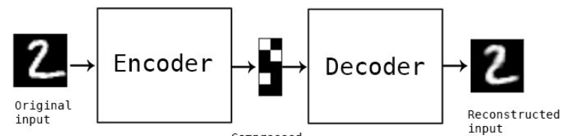
AVE（变成自编码器）是一个比GAN还要早的生成模型，它是AE（自编码器）的一种变体，下图是一个AE结构，它的输出是在还原输入，Encoder的输出就是编码，AE更多的用来做数据的压缩。

而VAE就可以用来生成新的东西了，VAE和AE的区别在于，AE不关心中间的编码形式，只关心输出是不是完全还原了输入，而VAE除此之外，还要控制中间编码向量的形式，如下所示。

当对z_log_var重新采样的时候，就能控制新的输出。

GAN和VAE

VAE一般采用MSE评估生成图像，即每一个像素上的均方差，这样会使生成的图像变得模糊。但是VAE由于自身是带条件控制的，所以VAE不会生成很多奇奇怪怪的图像。
GAN采用判别器评估生成的图像，由于没了均方误差损失，所以GAN生成图像更清晰，但是由于GAN很难训练，同时原始的GAN没有条件控制的能力，所以GAN生成的图像有些会很奇怪。
此外，由于GAN没有编码，所以它是一个随机噪声到图像的过程，而VAE是图到图的过程。
所以就有了将GAN和VAE结合的方法，《Autoencoding beyond pixels using a learned similarity metric》。

GAN和CNN

CNN就不用多说了，它和GAN也是独立的，GAN的结构可以用任意模型做判别器和生成器，不见得是CNN结构。但是由于CNN强大的特征自提取功能，不用来和GAN结合，简直太可惜了，所以第一个这么干的就是DCGAN，《Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks》，DCGAN解决了CNN用于GAN时不稳定的问题，于是到现在，几乎所有的GAN模型，都是用CNN做生成器和判别器。