集成学习Adaboost算法及python实现及sklearn包的调用
集成方法(ensemble method)
要获得好的集成,个体学习器应“好而不同”,即个体学习器要有一定的准确性(不能太坏),并且要有多样性(学习器间具有差异)。
集成方法主要可分为
个体学习器存在强依赖关系,必须串行生成的序列化方法(Boosting),
个体学习器不存在强依赖关系,可同时并行化方法(Bagging)。
- bagging 基于数据重抽样的分类器构建方法
在Bagging方法中,主要通过对训练数据集进行随机采样,以重新组合成不同的数据集,新数据集和旧数据集大小相等,利用弱学习算法对不同的新数据集进行学习,得到一系列的预测结果,对这些预测结果做平均或者投票做出最终的预测。注:随机森林算法是基于Bagging思想的机器学习算法。
- boosting
boosting和bagging很类似,但是boosting的分裂结果是基于所有分类器的加权求和结果的,每个权重代表的是对应分类器在上一轮迭代的成功度,而bagging的权重是相等的。
这族的算法工作机制蕾丝:先从初始训练集训练出一个集学习器。再根据基学习器的表现对样本分布进行调整,是的先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布训练下一个基学习器;如此反复,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数T,最后讲这些基学习器进行加权结合。
AdaBoost算法(Adaptive Boosting)和GBDT(Gradient Boost Decision Tree,梯度提升决策树)算法是基于Boosting思想的机器学习算法。在Boosting思想中是通过对样本进行不同的赋值,对错误学习的样本的权重设置的较大,这样,在后续的学习中集中处理难学的样本,最终得到一系列的预测结果,每个预测结果有一个权重,较大的权重表示该预测效果较好。
AdaBoost算法原理
能否用弱分类器和多个实力来构建一个强分类器,前一个基本分类器分错的样本会得到加强,加权后的全体样本再次被用来训练下一个基本分类器。同时,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
具体说来,整个Adaboost 迭代算法就3步:
- 初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权重:1/N。
- 训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权重就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。然后,权重更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
算法流程
步骤1. 首先,初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权重:1/N。
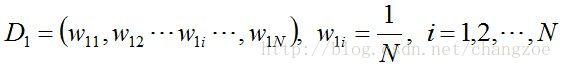
步骤2. 进行多轮迭代,用m = 1,2, …, M表示迭代的第多少轮
b. 计算Gm(x)在训练数据集上的分类误差率
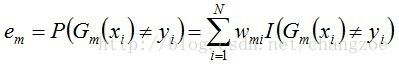 即:
即:

由上述式子可知,Gm(x)在训练数据集上的误差率em就是被Gm(x)误分类样本的权值之和。
c. 计算Gm(x)的系数,am表示Gm(x)在最终分类器中的重要程度(目的:得到基本分类器在最终分类器中所占的权重):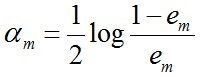
由上述式子可知,em <= 1/2时,am >= 0,且am随着em的减小而增大,意味着分类误差率越小的基本分类器在最终分类器中的作用越大。
d. 更新训练数据集的权值分布(目的:得到样本的新的权值分布),用于下一轮迭代
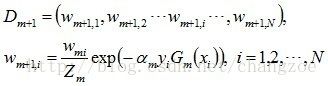
使得被基本分类器Gm(x)误分类样本的权值增大,而被正确分类样本的权值减小。就这样,通过这样的方式,AdaBoost方法能“聚焦于”那些较难分的样本上。
其中,Zm是规范化因子,使得Dm+1成为一个概率分布:
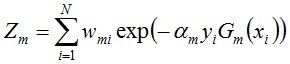
从而得到最终分类器,如下:
原理和例子
基于单层决策树构建弱分类器
单层决策树(decision stump)是一种简单的决策树桩
准备数据集
from numpy import *
from operator import*
import matplotlib.pyplot as plt
def loadSimpData():
datMat = matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels画出来数据集的示意图:
def showScatter(matrix, labels):
plt.figure(figsize=(8,6))
x1 = []; y1 = []; x2 = []; y2 = []
for i in range(len(labels)):
if labels[i] == 1.0:
x1.append(matrix[i, 0])
y1.append(matrix[i, 1])
else:
x2.append(matrix[i, 0])
y2.append(matrix[i, 1])
plt.scatter(x1, y1, marker='o',color='g', alpha=0.7, label='1.0')
plt.scatter(x2, y2, marker='^',color='red', alpha=0.7, label='-1.0')
plt.title('dataset')
plt.ylabel('variable Y')
plt.xlabel('Variable X')
plt.legend(loc='upper right')
plt.show()
datmat,classlabels=loadSimpData()
showScatter(datmat,classlabels)如图所示,我们要把两种图形分开:
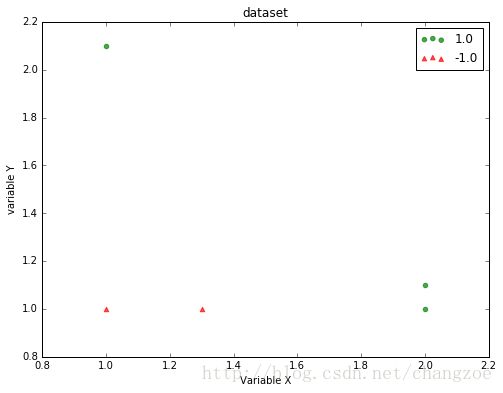
我们将多个单层决策树,构建一个对该数据集完全正确分类的分类器。
单层决策树生成函数
伪代码:
- 将最小错误率minError设为Inf(正无穷)
- 对于数据集的每一个特征:(第一层)
- 对每个补步长:(第二层)
- 对每个不等号:(第三层)
建立一颗决策树并用加权数据集对它进行测试
如果错误率低于minError,将当前决策树设为最佳单层决策树
- 对每个不等号:(第三层)
- 对每个补步长:(第二层)
- 返回最佳单层决策树
(共三层循环)
'''
通过阈值比较对数据进行分类的,所有在阈值一边的数据分到类别-1,而在另一边的数据分到类别1
'''
# dataMatirx:要分类的数据
# dimen:维度
# threshVal:阈值
# threshIneq:有两种,‘lt’=lower than,‘gt’=greater than
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray#beststump存储给定权重向量D时所得到的的最佳单层决策树的相关信息
#numSteps 用于在特征的所有可能值上进行便利
#bestClasEst 最佳单层决策树的判断
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print ("split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError))
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst拟运行一下看看~
D=mat(ones((5,1))/5)
buildStump(datmat,classlabels,D)({'dim': 0, 'ineq': 'lt', 'thresh': 1.3}, matrix([[ 0.2]]), array([[-1.],
[ 1.],
[-1.],
[-1.],
[ 1.]]))AdaBoost算法的实现
伪代码:
- 对每次迭代:
利用buildStump()函数找到最佳的单层决策树
将最佳单层决策树加入到单层决策树组
计算alpha
计算新的权重向量D
更新累计类别估计值
如果错误率大于0.0,退出循环
#函数尾部DS代表使用单层决策树为弱分类器
#aggClassEst记录每个数据点的类别估计累加值
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
#print("D:",D.T)
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
#print ("classEst: ",classEst.T)
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
#print ("aggClassEst: ",aggClassEst.T)
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
# print ("total error: ",errorRate)
if errorRate == 0.0: break
return weakClassArr,aggClassEst其中sign函数 -1 if x < 0, 0 if x==0, 1 if x > 0
multiply(3==4,1) >>>0
multiply(3==3,1) >>>1
测试以上程序:
classifierArray=adaBoostTrainDS(datmat,classlabels,9)
classifierArray
Out:
([{'alpha': 0.6931471805599453, 'dim': 0, 'ineq': 'lt', 'thresh': 1.3},
{'alpha': 0.9729550745276565, 'dim': 1, 'ineq': 'lt', 'thresh': 1.0},
{'alpha': 0.8958797346140273,
'dim': 0,
'ineq': 'lt',
'thresh': 0.90000000000000002}],
matrix([[ 1.17568763],
[ 2.56198199],
[-0.77022252],
[-0.77022252],
[ 0.61607184]]))基于AdaBoost分类
#datToClass待分类的样例
#clssifierArr 弱分类器组成的数组
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
#print (aggClassEst)
return sign(aggClassEst)看看实际运行结果
datarr,labelarr=loadSimpData()
classifierArr,est = adaBoostTrainDS(datarr,labelarr,30)
adaClassify([[5,5],[0,0],[1,2],[2,1]],classifierArr)matrix([[ 1.],
[-1.],
[ 1.],
[ 1.]])在实际数据集上应用AdaBoost算法
我们在马疝病数据集上应用AdaBoost分类器,利用AdaBoost预测患有疝病的马能不能存活
- 收集数据
- 准备数据:确保类别是+1和-1
- 分析数据
- 训练算法:在数据上,利用adaBoostTrainDS()函数训练一系列的分类器
- 测试算法:对测试集合
- 使用算法
datArr,labelArr=loadDataSet('C:/Users/elenawang/Documents/machinelearninginaction/Ch07/horseColicTraining2.txt')
classifierArray,est=adaBoostTrainDS(datArr,labelArr,10)
testArr,testLabelArr=loadDataSet('C:/Users/elenawang/Documents/machinelearninginaction/Ch07/horseColicTest2.txt')
prediction10=adaClassify(testArr,classifierArray)
errArr = mat(ones((67,1)))
errArr[prediction10!=mat(testLabelArr).T].sum()/670.23880597014925373| 分类器数目 | 训练错误率 | 测试错误率 |
|---|---|---|
| 1 | 0.28 | 0.27 |
| 10 | 0.23 | 0.24 |
| 50 | 0.19 | 0.21 |
| 100 | 0.19 | 0.22 |
| 500 | 0.16 | 0.25 |
| 1000 | 0.14 | 0.31 |
存在过拟合现象。
回到数据集本身,考虑将缺失的值不化为0而转化为其他值,如平均值等,再次尝试。
sklearn包中有关AdaBoost使用
常用的组合
BaggingClassifier: Bagging分类器组合
BaggingRegressor: Bagging回归器组合
AdaBoostClassifier: AdaBoost分类器组合
AdaBoostRegressor: AdaBoost回归器组合
GradientBoostingClassifier:GradientBoosting分类器组合
GradientBoostingRegressor: GradientBoosting回归器组合
ExtraTreeClassifier:ExtraTree分类器组合
ExtraTreeRegressor: ExtraTree回归器组合
RandomTreeClassifier:随机森林分类器组合
RandomTreeRegressor: 随机森林回归器组合使用类:
class sklearn.ensemble.AdaBoostClassifier(base_estimator=None, n_estimators=50,learning_rate=1.0, algorithm='SAMME.R', random_state=None)
参数介绍:
- base_estimator :(default=DecisionTreeClassifier)
选择哪种若分类器,scikit-learn中的分类器都可以
我们常用的一般是CART决策树或者神经网络MLP。默认是决策树,即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier,而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor
- n_estimators :integer, (default=50)
最大迭代次数,一般来说n_estimators太小,容易欠拟合,n_estimators太大,又容易过拟合,一般选择一个适中的数值。默认是50。在实际调参的过程中,我们常常将n_estimators和下面介绍的参数learning_rate一起考虑。
- learning_rate :float, (default=1.0) 迭代次数的每个弱分类器权重设置参数
- algorithm : {‘SAMME’, ‘SAMME.R’},(default=’SAMME.R’)
’SAMME.R’的话弱分类器需要支持概率预测,比如逻辑回归;‘SAMME’这个是针对离散的变量。
类中方法:
fit(X, y[, sample_weight]) #拟合模型
predict(X) #求预测值
predict_proba(X)
score(X, y[, sample_weight]) class sklearn.ensemble.AdaBoostRegressor(base_estimator=None, n_estimators=50,learning_rate=1.0, loss='linear', random_state=None)
参数:
- loss:这个参数只有AdaBoostRegressor有,Adaboost.R2算法需要用到。有线性‘linear’,平方‘square’和指数 ‘exponential’三种选择,默认是线性,一般使用线性就足够了,除非你怀疑这个参数导致拟合度不好。这个值的意义在原理篇我们也讲到了,它对应了我们对第k个弱分类器的中第i个样本的误差的处理,即:如果是线性误差,eki=|yi−Gk(xi)|Ekeki=|yi−Gk(xi)|Ek;如果是平方误差,则eki=(yi−Gk(xi))2E2keki(yi−Gk(xi))2Ek2,如果是指数误差,则eki=1−exp(−yi+Gk(xi))Ek)eki=1−exp(−yi+Gk(xi))Ek),EkEk为训练集上的最大误差Ek=max|yi−Gk(xi)|i=1,2...mEk=max|yi−Gk(xi)|i=1,2...m
- base_estimator :(default=DecisionTreeClassifier)
选择哪种若分类器,scikit-learn中的分类器都可以
我们常用的一般是CART决策树或者神经网络MLP。默认是决策树,即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier,而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor
- learning_rate :float, (default=1.0) 迭代次数的每个弱分类器权重设置参数
- n_estimators :integer, (default=50)
最大迭代次数,一般来说n_estimators太小,容易欠拟合,n_estimators太大,又容易过拟合,一般选择一个适中的数值。默认是50。在实际调参的过程中,我们常常将n_estimators和下面介绍的参数learning_rate一起考虑DecisionTreeClassifier和DecisionTreeRegressor的参数重要的如下:
1) 划分时考虑的最大特征数max_features: 可以使用很多种类型的值,默认是"None",意味着划分时考虑所有的特征数;如果是"log2"意味着划分时最多考虑log2Nlog2N个特征;如果是"sqrt"或者"auto"意味着划分时最多考虑N−−√N个特征。如果是整数,代表考虑的特征绝对数。如果是浮点数,代表考虑特征百分比,即考虑(百分比xN)取整后的特征数。其中N为样本总特征数。一般来说,如果样本特征数不多,比如小于50,我们用默认的"None"就可以了,如果特征数非常多,我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数,以控制决策树的生成时间。
2) 决策树最大深max_depth: 默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。
3) 内部节点再划分所需最小样本数min_samples_split: 这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
4) 叶子节点最少样本数min_samples_leaf: 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
5)叶子节点最小的样本权重和min_weight_fraction_leaf:这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝。 默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
6) 最大叶子节点数max_leaf_nodes: 通过限制最大叶子节点数,可以防止过拟合,默认是''None'',即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制,具体的值可以通过交叉验证得到。# -*- encoding:utf-8 -*-
'''
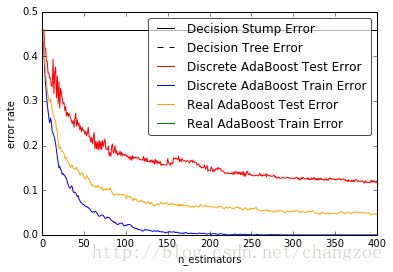
本例是Sklearn网站上的关于决策树桩、决策树、
和分别使用AdaBoost—SAMME和AdaBoost—SAMME.R的AdaBoost算法
在分类上的错误率。
这个例子基于Sklearn.datasets里面的make_Hastie_10_2数据库。
取了12000个数据,其他前10000个作为训练集,后面2000个作为了测试集。
'''
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import zero_one_loss
from sklearn.ensemble import AdaBoostClassifier
import time
a=time.time()
n_estimators=400
learning_rate=1.0
X,y=datasets.make_hastie_10_2(n_samples=12000,random_state=1)
X_test,y_test=X[10000:],y[10000:]
X_train,y_train=X[:2000],y[:2000]
#决策树桩
dt_stump=DecisionTreeClassifier(max_depth=1,min_samples_leaf=1)
dt_stump.fit(X_train,y_train)
dt_stump_err=1.0-dt_stump.score(X_test,y_test)
#决策树
dt=DecisionTreeClassifier(max_depth=9,min_samples_leaf=1)
dt.fit(X_train,y_train)
dt_err=1.0-dt.score(X_train,y_test)
#决策树桩的生成
ada_discrete=AdaBoostClassifier(base_estimator=dt_stump,learning_rate=learning_rate,
n_estimators=n_estimators,algorithm='SAMME')
ada_discrete.fit(X_train,y_train)
ada_real=AdaBoostClassifier(base_estimator=dt_stump,learning_rate=learning_rate,
n_estimators=n_estimators,algorithm='SAMME.R')#相比于ada_discrete只改变了Algorithm参数
ada_real.fit(X_train,y_train)
fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot([1,n_estimators],[dt_stump_err]*2,'k-',label='Decision Stump Error')
ax.plot([1,n_estimators],[dt_err]*2,'k--',label='Decision Tree Error')
ada_discrete_err=np.zeros((n_estimators,))
for i,y_pred in enumerate(ada_discrete.staged_predict(X_test)):
ada_discrete_err[i]=zero_one_loss(y_pred,y_test)#0-1损失,类似于指示函数
ada_discrete_err_train=np.zeros((n_estimators,))
for i,y_pred in enumerate(ada_discrete.staged_predict(X_train)):
ada_discrete_err_train[i]=zero_one_loss(y_pred,y_train)
ada_real_err=np.zeros((n_estimators,))
for i,y_pred in enumerate(ada_real.staged_predict(X_test)):
ada_real_err[i]=zero_one_loss(y_pred,y_test)
ada_real_err_train=np.zeros((n_estimators,))
for i,y_pred in enumerate(ada_real.staged_predict(X_train)):
ada_discrete_err_train[i]=zero_one_loss(y_pred,y_train)
ax.plot(np.arange(n_estimators)+1,ada_discrete_err,label='Discrete AdaBoost Test Error',color='red')
ax.plot(np.arange(n_estimators)+1,ada_discrete_err_train,label='Discrete AdaBoost Train Error',color='blue')
ax.plot(np.arange(n_estimators)+1,ada_real_err,label='Real AdaBoost Test Error',color='orange')
ax.plot(np.arange(n_estimators)+1,ada_real_err_train,label='Real AdaBoost Train Error',color='green')
ax.set_ylim((0.0,0.5))
ax.set_xlabel('n_estimators')
ax.set_ylabel('error rate')
leg=ax.legend(loc='upper right',fancybox=True)
leg.get_frame().set_alpha(0.7)
b=time.time()
print ('total running time of this example is :',(b-a))
plt.show()链接1
链接2
怎么调参看这个
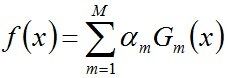
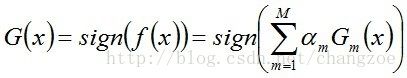
![score(X, y[, sample_weight])](http://img.e-com-net.com/image/info8/dd450e78427340d680ee964c08502b2e.jpg)