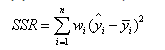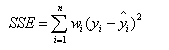Dummy coding

1.什么是Dummy Coding（虚拟编码）

虚拟编码为不同的估计模型提供了一种使用分类变量的方法，比如线性回归模型。当自变量中存在无序多分类的变量，比如血型，分为A、B、O、AB，因为它们之间不存在等级关系，所以在引入回归时，不能直接用1、2、3、4来表示，需要将血型转化为哑变量，并且要设置一个参照。虚拟编码使用0或1来表达所有类别的必要信息，这些取值并不代表数量的大小，仅仅表示不同的类别。下面的例子说明如何引入dummy coding。如下图所示，在四个类中各有四个观测变量，对这组数据进行线性回归：

Group	G1	G2	G3	G4
	1	2	5	10
	3	3	6	10
	2	4	4	9
	2	3	5	11
Mean	2	3	5	10

这个例子我们需要使用三个虚拟编码变量。通常来说，k个类别需要k-1个虚拟变量。每一个虚拟变量有一个自由度，所以k个类别有k-1个自由度，与方差分析类似。

我们将上例使用的三个虚拟变量分别命名为d1，d2和d3。类别1的每一个观测量上的d1位将被编码为1，其余的类别变量编码为0。同样的，类别2中的每一个观测量的d2位编码为1，其余位编码为0。这里并不需要第四个虚拟变量d4，因为d1~d3三个虚拟变量已经能够决定观测量属于哪一个类别。

以下是我们对上述观测量的虚拟编码：

Y  Group d1   d2   d3

1   1   1    0    0

3   1   1    0    0

2   1   1    0    0

2   1   1    0    0

2   2   0    1    0

3   2   0    1    0

4   2   0    1    0

3   2   0    1    0

5   3   0    0    1

6   3   0    0    1

4   3   0    0    1

5   3   0    0    1

10  4   0    0    0

10  4   0    0    0

9   4   0    0    0

11  4   0    0    0

所有虚拟变量编码为0的类别定义为参照组。除参照组外，其余每个类别里的观测量编码有且只有一个虚拟变量的值为1。通过虚拟编码，回归模型的常数等于参考组的均值。在上例中，常数的值为10等于类别4的均值。每个虚拟变量在回归模型中的系数为该类别的均值与参照组的均值之差。在本例中，类别1的均值为2,与10的差值为-8，正好是d1的回归系数。本例中线性回归的结果如下表所示。

F(3, 12)= 76.00  P = 0.0000  R-squared = 0.95

y	Coef.	Std.Err.	t	p>|t|
D1	-8	.5773503	-13.86	0.000
D2	-7	.5773503	-12.12	0.000
D3	-5	.5773503	-8.66	0.000
constant	10	.4082483	24.49	0.000

不论选择哪个类别为参考组，最后生成的模型都具有相同的F-ratio和R-squared值。

 2.为什么要使用虚拟编码

虚拟编码中的变量又叫哑变量、虚设变量、名称变量（Dummy variables）。用以反映质的属性的一个人工变量，是量化了的自变量，通常取值为0或1。引入哑变量可使线形回归模型变得更复杂，但对问题描述更简明，一个方程能达到俩个方程的作用，而且接近现实。

引入哑变量的目的是将不能够定量处理的变量量化，如职业、性别对收入的影响，战争、自然灾害对GDP的影响，季节对某些产品（如冷饮）销售的影响等等。这种“量化”通常是通过引入“哑变量”来完成的。根据这些因素的属性类型，构造只取“0”或“1”的人工变量，记为D。

模型中引入虚拟变量的作用

1、分离异常因素的影响，例如分析我国GDP的时间序列，必须考虑“文革”因素对国民经济的破坏性影响，剔除不可比的“文革”因素。

2、检验不同属性类型对因变量的作用，例如工资模型中的文化程度、季节对销售额的影响。

3、提高模型的精度，相当于将不同属性的样本合并，扩大了样本容量（增加了误差自由度，从而降低了误差方差）。

3.一个例子

季节数据模型

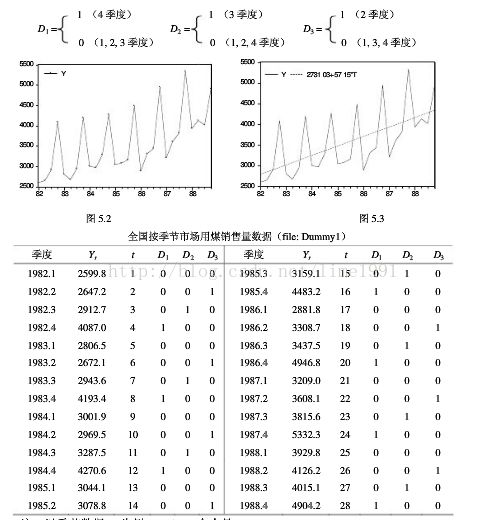
我国市场用煤销量的季节性数据（1982-1988，《中国统计年鉴》1987，1989）见下图与表。由于受取暖用煤的影响，每年第四季度的销售量大大高于其它季度。鉴于是季节数据可设三个季节变量如下：

以时间t为解释变量（1982年1季度取t = 1）的煤销售量（y）模型如下：

y = 2431.20 + 49.00 t + 1388.09*D1 +201.84*D2 + 85.00*D3           (1)

(26.04)   (10.81)             (13.43)              (1.96)            (0.83)

R2 = 0.95, DW = 1.2, s.e. = 191.7, F=100.4, T=28, t0.05 (28-5) = 2.07

由于D2，D3的系数没有显著性，说明第2，3季度可以归并入基础类别第1季度。于是只考虑加入一个虚拟变量D1，把季节因素分为第四季度和第一、二、三季度两类。从上式中剔除虚拟变量D2，D3，得煤销售量（y）模型如下： 

y = 2515.86 + 49.73 t + 1290.91*D1                                                                 (2)

(32.03)   (10.63)             (14.79)

R2 = .94, DW = 1.4, s.e. = 198.7, F =184.9, T=28, t0.05 (25) = 2.06

若不采用虚拟变量，得回归结果如下， 

     y = 2731.03 + 57.15*t                                                                                  (3)                     

          (11.6)      (4.0) 

        R2 = 0.38, DW = 2.5, s.e. = 608.8, T = 28, t0.05 (26) = 2.06 

与（2）式相比，回归式（3）显得很差。

4.一些科普知识

博主的《概率论与数理统计》早已经还给了当年的大学老师，一些常用知识百度后补充如下。

4.1 控制变量和解释变量

解释变量与控制变量都是自变量，为了突出研究的问题进行了区分。

解释变量：是指着重研究的自变量，是研究者重点考查对因变量有何影响的变量。

控制变量：是指与特定研究目标无关的非研究变量，即除了研究者重点研究的解释变量和需要测定的因变量之外的变量，是研究者不想研究，但会影响研究结果的，需要加以考虑的变量。

如上例中时间t为解释变量，D1~D3为控制变量。

4.2 自由度

以样本的统计量来估计总体的参数时， 样本中独立或能自由变化的资料的个数，称为该统计量的自由度。首先，在估计总体的平均数时，由于样本中的 n 个数都是相互独立的，从其中抽出任何一个数都不影响其他数据，所以其自由度为n。    在估计总体的方差时，使用的是离差平方和。只要n-1个数的离差平方和确定了，方差也就确定了；因为在均值确定后，如果知道了其中n-1个数的值，第n个数的值也就确定了。这里，均值就相当于一个限制条件，由于加了这个限制条件，估计总体方差的自由度为n-1。

4.3 R-squared确定系数

在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的。

(1)SSR：Sum of squares ofthe regression，即预测数据与原始数据均值之差的平方和，公式如下

(2) SSE(和方差): The sum of squares due to error

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。

(3)SST：Total sum ofsquares，即原始数据和均值之差的平方和，公式如下

SST=SSE+SSR。而“确定系数”定义为SSR和SST的比值，故

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。