Python机器学习及实践——无监督学习经典模型（K-means）

无监督学习着重于发现数据本身的分布特点。与监督学习不同，无监督学习不需要对数据进行标记。

从功能角度讲，无监督学习模型可以帮助我们发现数据的“群落”，同时也可以寻找“离群”的样本；另外对于特征维度非常高的数据样本，我们同样可以通过无监督的学习对数据进行降维，保留最具有区分性的低纬度特征。

数据聚类是无监督学习的主流应用之一，最为经典并且易用的聚类模型，要属K均值算法。该算法要求我们预先设定聚类的个数，然后不断更新聚类中心；经过几轮这样的迭代，最后的目标就是要让所有数据点到其所属聚类中心的平方和趋于稳定。

模型介绍：

算法执行的过程分为4个阶段：1、首先，随机布设K个特征空间内的点作为初始的聚类中心；2、然后，对于每个数据的特征向量，从K个聚类中心中寻找距离最近的一个，并且把该数据标记为从属于这个聚类中心；3、接着，在所有的数据上都被标记过聚类中心后，根据这些数据新分配的类簇，重新对K个聚类中心做计算；4、如果一轮下来，所有的数据点从属的聚类中心与上一次分配的类簇没有变化，那么迭代可以停止，否则回到第2步继续循环。

数据介绍：

此处我们使用手写体数字图像数据。sklearn内部集成的仅仅是原数据的一部分，但本篇我们将使用完整的手写体图像数据。

这份数据分为两个集合，其中训练样本3823条，测试样本1797条；图像数据通过8 X 8的像素矩阵表示，共有64个像素维度；1个目标维度用来标记每个样本代表的数字类别。该数据没有缺失的特征值，并且不论是训练还是测试样本，在数字类别方面都采样的非常平均。

使用如下代码对这份数据的图像特征进行K-mean聚类：

# 分别导入numpy、matplotlib以及pandas，用于数学运算、作图以及数据分析。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 使用pandas分别读取训练数据与测试数据集。
digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra', header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes', header=None)

# 从训练与测试数据集上都分离出64维度的像素特征与1维度的数字目标。
X_train = digits_train[np.arange(64)]
y_train = digits_train[64]

X_test = digits_test[np.arange(64)]
y_test = digits_test[64]

# 从sklearn.cluster中导入KMeans模型。
from sklearn.cluster import KMeans

# 初始化KMeans模型，并设置聚类中心数量为10。
kmeans = KMeans(n_clusters=10)
kmeans.fit(X_train)

# 逐条判断每个测试图像所属的聚类中心。
y_pred = kmeans.predict(X_test)

性能测评：

大家可能会困惑如何评估聚类算法的性能，特别是应用在没有标注类别的数据集上的时候。针对不同的数据特点，这里提供两种方式。

1. 如果被评估的数据本身带有正确的类别信息，可以使用ARI。ARI指标与分类问题中计算准确性的方法类似，同时也兼顾到了类簇无法和分类标记一一对应的问题。下述代码使用ARI进行K-means聚类性能评估：

# 从sklearn导入度量函数库metrics。
from sklearn import metrics
# 使用ARI进行KMeans聚类性能评估。
print metrics.adjusted_rand_score(y_test, y_pred)

  0.665144851397

    2.如果被用于评估的数据没有所属类别，那么习惯使用轮廓系数来度量聚类结果的质量。轮廓系数同时兼顾了聚类的凝聚度和分离度，用于评估聚类的效果并且取值范围为[-1,1]。轮廓系数值越大，表示聚类效果越好。

轮廓系数的具体计算方法此处不叙述。

为说明轮廓系数与聚类效果的关系，使用下面代码对一组简单的数据进行分析。

# 导入numpy。
import numpy as np
# 从sklearn.cluster中导入KMeans算法包。
from sklearn.cluster import KMeans
# 从sklearn.metrics导入silhouette_score用于计算轮廓系数。
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt

# 分割出3*2=6个子图，并在1号子图作图。
plt.subplot(3,2,1)

# 初始化原始数据点。
x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(zip(x1, x2)).reshape(len(x1), 2)

# 在1号子图做出原始数据点阵的分布。
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Instances')
plt.scatter(x1, x2)

colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'b']
markers = ['o', 's', 'D', 'v', '^', 'p', '*', '+']

clusters = [2, 3, 4, 5, 8]
subplot_counter = 1
sc_scores = []
for t in clusters:
    subplot_counter += 1
    plt.subplot(3, 2, subplot_counter)
    kmeans_model = KMeans(n_clusters=t).fit(X)
    for i, l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l], ls='None')
    plt.xlim([0, 10])
    plt.ylim([0, 10])
    sc_score = silhouette_score(X, kmeans_model.labels_, metric='euclidean')
    sc_scores.append(sc_score)

# 绘制轮廓系数与不同类簇数量的直观显示图。
    plt.title('K = %s, silhouette coefficient= %0.03f' %(t, sc_score))
    
# 绘制轮廓系数与不同类簇数量的关系曲线。
plt.figure()
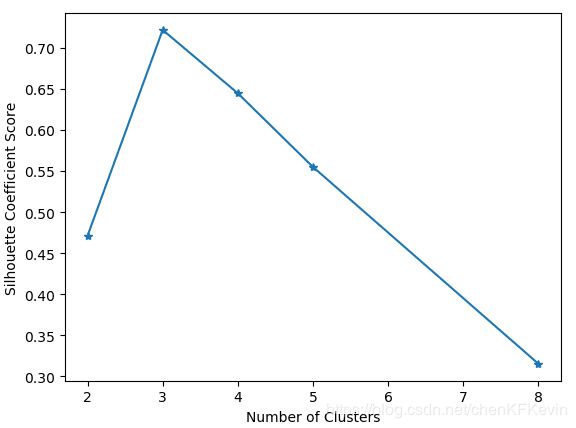
plt.plot(clusters, sc_scores, '*-')
plt.xlabel('Number of Clusters')
plt.ylabel('Silhouette Coefficient Score')

plt.show()

从上图可知，当聚类中心数量为3的时候，轮廓系数最大；此时，我们观察到聚类中心数量为3时，符合数据的分布特点，的确是相对较为合理的分簇数量。

特点分析：

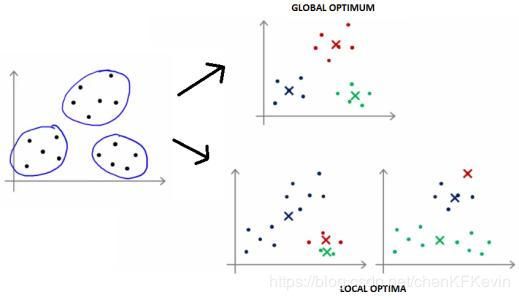
K-means聚类模型所采用的迭代式算法，直观易懂并且非常实用。只有两个缺点：1、容易收敛到局部最优解；2、需要预先设定簇的数量。

下图展示了什么叫局部最优解，这是算法自身的理论缺陷所造成的，无法轻易地从模型设计上弥补；却可以通过执行多次K-means算法来挑选性能表现更好的初始中心点。

此处，介绍一种“肘部”观察法用于粗略地预估相对合理的类簇个数。因为K-means模型最终期望所有数据点到其所属的类簇距离的平方和趋于稳定，所以我们可以通过观察这个数值随着K的走势来找出最佳的类簇数量。理想条件下，这个折线在不断下降并且趋于平稳的过程中会有斜率的拐点，同时意味着从这个拐点对应的K值开始，类簇中心的增加不会过于破坏数据聚类的结构。

以下述代码为例，如下图所示随机采样三个类簇的数据点，可见类簇数量为1或2的时候，样本距所属类簇的平均距离的下降速度很快，这说明更改K值会让整体聚类结构有很大改变，也意味着新的聚类数量让算法有更大的收敛空间，这样的K值不能反映真是的类簇数量。而当K=3时，平均距离的下降速度有了显著放缓，这意味着进一步增加K值不再会有利于算法的收敛，也同时暗示着K=3是相对最佳的类簇数量。

“肘部”观察法示例：

# 导入必要的工具包。
import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

# 使用均匀分布函数随机三个簇，每个簇周围10个数据样本。
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(5.5, 6.5, (2, 10))
cluster3 = np.random.uniform(3.0, 4.0, (2, 10))

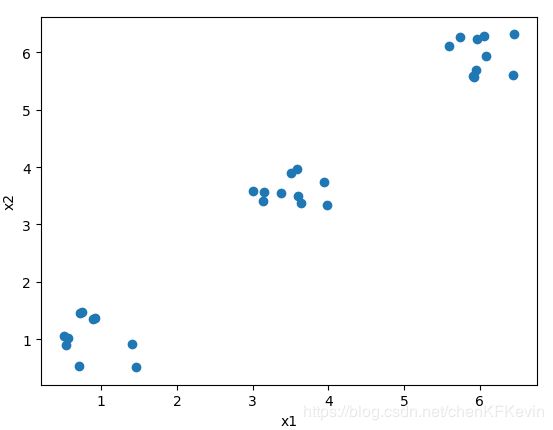
# 绘制30个数据样本的分布图像。
X = np.hstack((cluster1, cluster2, cluster3)).T
plt.scatter(X[:,0], X[:, 1])
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()


# 测试9种不同聚类中心数量下，每种情况的聚类质量，并作图。
K = range(1, 10)
meandistortions = []

for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1))/X.shape[0])
    
plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Average Dispersion')
plt.title('Selecting k with the Elbow Method')
plt.show()