深度神经网络(DNN)Deep Neural Networks 介绍
Some of the content for this lecture is borrowed from Hugo Larochelle
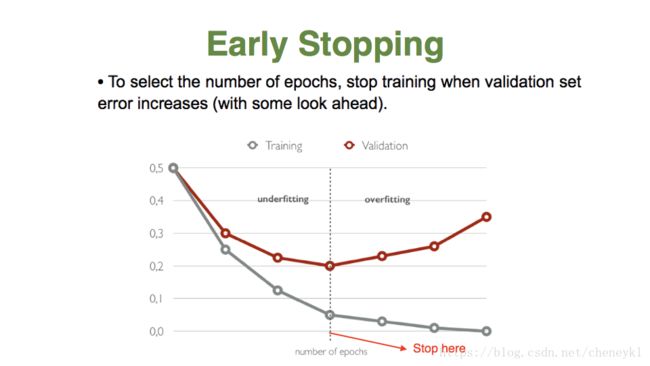
神经网络相对于训练集:太小(欠拟合),找到的规律模型未能够很好的捕捉数据特征,不能很好的拟合数据;太大(过拟合),记住的规律太多,太具体死板地记住训练集,不够抽象。
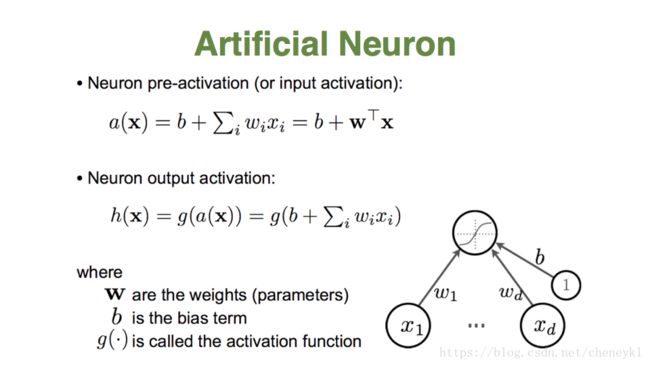
单个神经元的作用:把一个n纬的向量空间用一个超平面分成两部分(称之为判断边界),给定一个输入向量,神经元能判断出这个向量位于超平面的哪一边。b+wTx=0 就是超平面方程。
x1,x2,x3.....是输入特征向量的各个分量
w1,w2,w3....是各神经元各突触的权值
b:神经元偏置
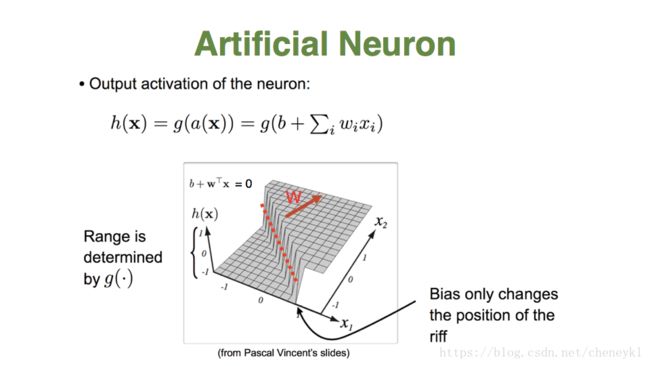
二维可视化激活函数表示图,W向量决定两类情况范围区别的基本方向,b变大,超平面会向相反的方向移动。
图中红色虚线就是超平面,w方向和超平面垂直
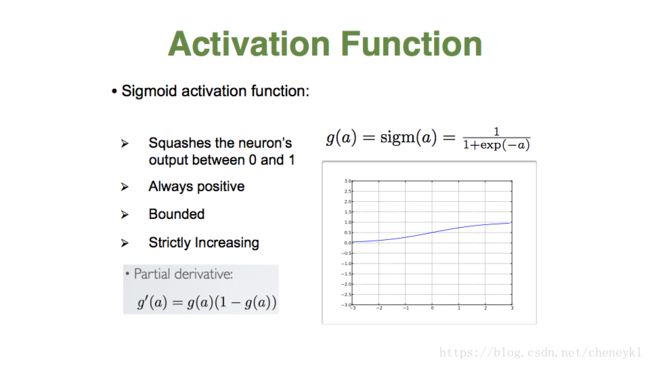
Sigmoid 激活函数,特点:可以将输出压缩到0-1的范围;总是正数;有界;严格递增
缺点:会出现梯度消失,这个函数的导数是g(a)(1-g(a)),最大值是1/4,所以每一层向前传递都会至少3/4的梯度损失。
激活函数的意义:
如果不加激活函数,无论多少的层隐层,最终的结果还是原始输入的线性变化,这样一层隐层就能达到效果,就没有多层感知器的意义了,所以每个隐层都配有激活函数,提供非线性的变化。
ReLU激活函数,修正线性激活函数
特点:非负;将神经元变得稀疏;没上界;严格递增
优点:可以防止梯度消失,其导数是1
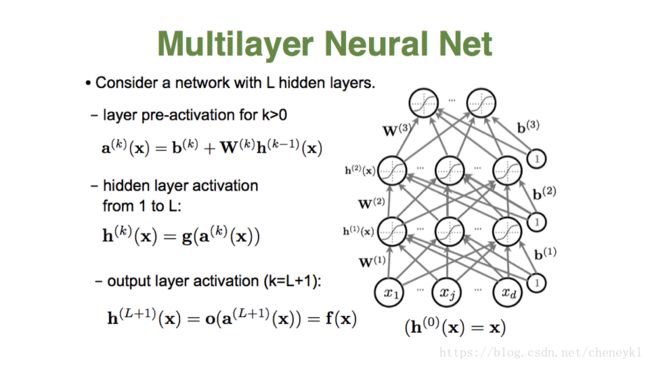
前馈神经网络,是指链接图无闭环或者回路。单隐层神经网络,只有一个隐藏层。
偏置单元无输入,w(1) 3*3 , w(2) 1*3 , S(l) 表示第l层节点个数,不包括偏置单元。
w(1)i,j 表示第一层的 j 单元和第二层的 i 单元链接权重
这个例子可以解释XOR抑或门
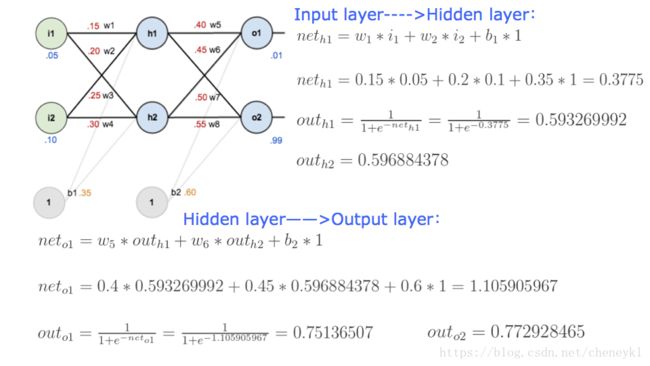
前向传播的例子
扩展到多个隐藏层
通用近似定理:单隐层神经网络如果有线性输出层,可以以任何精度逼近任何连续函数,只要隐层神经元的个数足够多。
神经网络调参的形象比喻,磨合就是不断找到更好的参数值
theta 是所有参数的集合
关于训练样本集的平均损失。
经验风险最小化(empirical risk minimization,ERM)的策略认为,经验风险最小的模型是最优的模型。根据这一策略,按照经验风险最小化求最优模型就是求解最优化问题:但是,当样本容量很小时,经验风险最小化学习的效果就未必很好,会产生过拟合现象。而结构风险最小化(structural risk minimization, SRM)是为了防止过拟合而提出的策略。结构风险最小化等价于正则化。结构风险在经验风险的基础上加上表示模型复杂度的正则化项。在假设空间、损失函数以及训练集确定的情况下,结构风险的定义是:
其中,J(f)为模型的复杂度,是定义在假设空间上的泛函。模型f越复杂,复杂度J(f)就越大。也就是说,复杂度表示了对复杂模型的惩罚。结构风险小的模型往往对训练数据和未知的测试数据都有较好的预测。比如,贝叶斯估计中的最大后验概率估计(MAP)就是结构风险最小化的例子。当模型是条件概率分布,损失函数是对数损失函数,模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大后验概率估计。
结构风险最小化的策略认为结构风险最小的模型是最优的模型。所以求解模型,就是求解最优化问题:
随机梯度下降:
不直接计算梯度精确值,而是用梯度无偏差估计来替代梯度,随机化整个数据集,每次迭代仅选择一个训练样本去计算代价函数的梯度,然后更新参数,优点是计算速度很快,缺点是精度受到影响
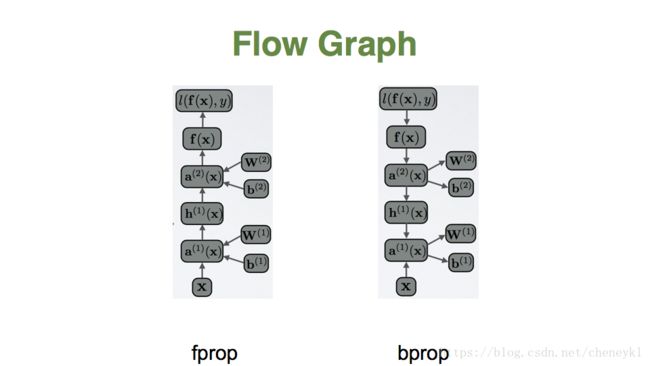
前向传播和反向传播图示。
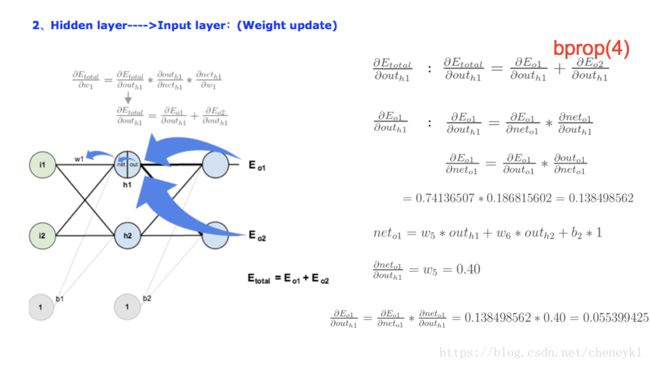
下面是反向传播的例子,详细计算过程:
模型选择,网格搜索或者随机搜索,网格搜索就是尝试所有的参数组合,随机组合就是随机尝试几组参数组合,选择这里面最好的组合
在上述的批梯度的方式中每次迭代都要使用到所有的样本,对于数据量特别大的情况,如大规模的机器学习应用,每次迭代求解所有样本需要花费大量的计算成本。是否可以在每次的迭代过程中利用部分样本代替所有的样本呢?基于这样的思想,便出现了mini-batch的概念。
假设训练集中的样本的个数为1000,则每个mini-batch只是其一个子集,假设,每个mini-batch中含有10个样本,这样,整个训练数据集可以分为100个mini-batch。
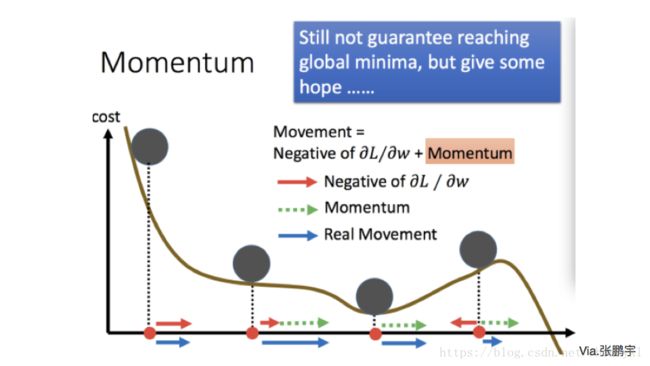
其中 即momentum系数,通俗的理解上面式子就是,如果上一次的momentum(即 )与这一次的负梯度方向是相同的,那这次下降的幅度就会加大,所以这样做能够达到加速收敛的过程。

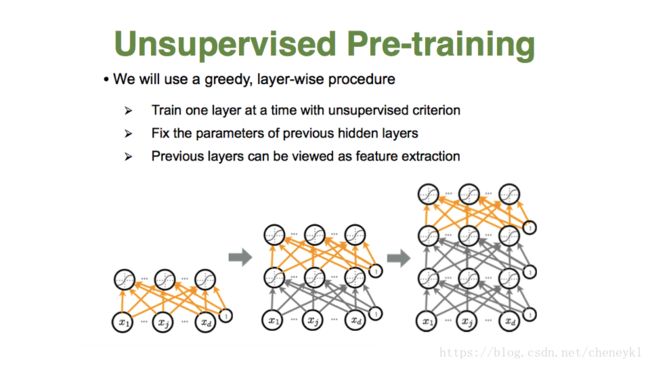
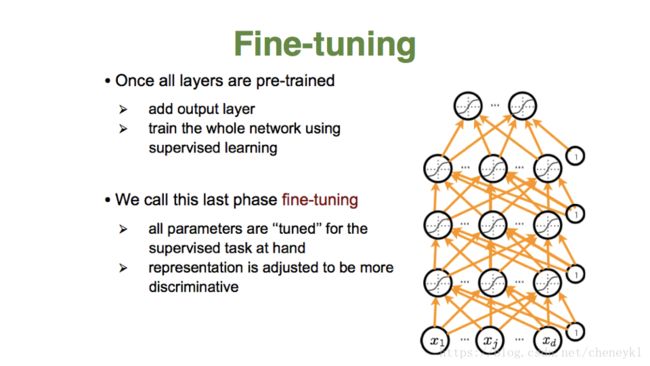
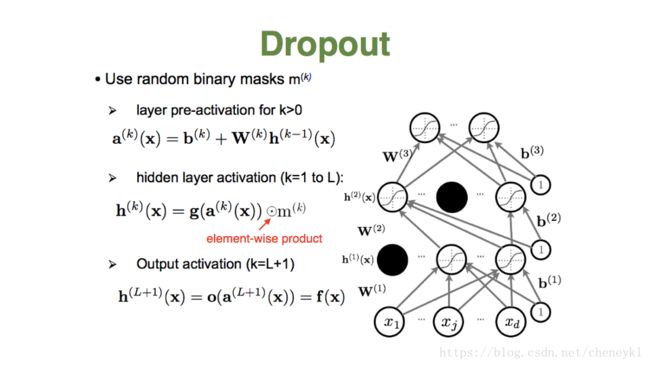
解决过拟合:无监督预训练;dropout
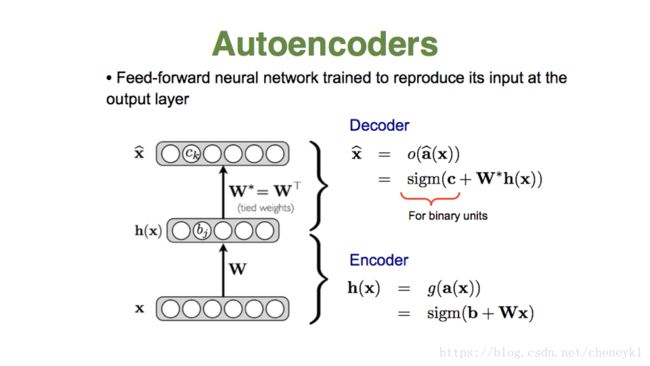
解码器、编码器
dropout:模型训练时,随机让网络某些隐藏层结点的权重不工作,不工作的结点可暂时认为不是网络结构的一部分,但是权重保留下来,不更新,因为下次样本输入时又可能会继续工作。
能减少神经元之间的共适性,一个神经元不能依赖其他特定的神经元,所以不得不去学习随机子集神经元间复样性的有用连接。
即:减少权重连接,增加网络模型在缺失个体连接信息情况下的鲁棒性。
欠拟合:BN,加速训练,解决梯度消失的问题