大数乘法的几种算法分析及比较(2014腾讯南京笔试题)
1.题目
编写两个任意位数的大数相乘的程序,给出计算结果。
2.题目分析
该题相继被ACM、华为、腾讯等选作笔试、面试题,若无准备要写出这种程序,还是要花一定的时间的。故,觉得有必要深入研究一下。搜索了网上的大多数该类程序和算法,发现,大数乘法主要有模拟手工计算的普通大数乘法,分治算法和FFT算法。其中普通大数乘法占据了90%以上,其优点是空间复杂度低,实现简单,时间复杂度为O(N²),分治算法虽然时间复杂度降低为, ![]()
但其实现需要配 合字符串模拟加减法操作,实现较为复杂,
参考博客1http://cnn237111.blog.51cto.com/2359144/1201901
FFT算法则更为复杂,较少适用,有兴趣
参考博客2 http://blog.csdn.net/hondely/article/details/6938497
和博客3http://blog.csdn.net/jackyguo1992/article/details/12613287。
普通大数乘法算法,主要有逐位相乘处理进位法、移位进位法,下面对其进行介绍并优化。
3.题目解答
3.1 逐位相乘处理进位法
参考博客4的思路
乘积是逐位相乘,也就是aibj,结果加入到积C的第i+j位,最后处理进位即可,例如:A =17 = 1*10 + 7 = (7,1)最后是十进制的幂表示法,幂次是从低位到高位,以下同。B=25 = 2*10 + 5 = (5, 2);C = A * B = (7 * 5, 1 * 5 + 2 * 7, 1 * 2) = (35, 19, 2) = (5, 22, 2) = (5, 2. 4)=425。
原博客的思路为:
(1)转换并反转,字符串转换为数字并将字序反转;
(2)逐位相乘,结果存放在result_num[i+j]中;
(3)处理进位,消除多余的0;
(4)转换并反转,将计算结果转换为字符串并反转。
原博客中采用指针参数传递,字符串长度有限制,改为通过string传参数,按原思路编程如下:
头文件和数据结构:
#include
#include
#include
#include
using namespace std;
struct bigcheng
{
vector a;
vector b;
string result_str;
};
void chartonum(string a,string b,bigcheng &tempcheng);//字符串转换为数字并反转
void multiply(bigcheng &tempchengh,vector &result_num);//逐位相乘,处理进位消除多余的0
void numtochar(bigcheng &tempcheng,vector &result_num);//将计算结果转换为字符串并反转
(1)转换并反转,字符串转换为数字并将字序反转;
void chartonum(string a,string b,bigcheng &tempcheng)
{
int size_a=a.size();
int size_b=b.size();
for (int i=size_a-1;i>=0;i--)
{
tempcheng.a.push_back(a[i]-'0');
}
for (int i=size_b-1;i>=0;i--)
{
tempcheng.b.push_back(b[i]-'0');
}
}
(2)逐位相乘,结果存放在result_num[i+j]中;
(3)处理进位,消除多余的0;代码为:
void multiply(bigcheng &tempcheng,vector &result_num)
{
for (unsigned int i=0;i=0;i--)
{
if (result_num[i]!=0)
{
break;
}
else
result_num.pop_back();
}
int c=0;
for (unsigned int i=0;i (4)转换并反转,将计算结果转换为字符串并反转。
void numtochar(bigcheng &tempcheng,vector &result_num)
{ int size=result_num.size();
for (unsigned int i=0;i
主函数为:
int main()
{
bigcheng tempcheng;
string a,b;
cin>>a>>b;
chartonum(a,b,tempcheng);
vector resultnum(a.size()+b.size(),0);
multiply(tempcheng,resultnum);
numtochar(tempcheng,resultnum);
cout<
上面的思路还是很清晰的,但代码有些过长,考虑优化如下:
(1)上述思路是先转换反转,其实无需先将全部字符串转换为数字的,可即用即转,节约空间;
(2)无需等到逐位相乘都结束,才处理进位,可即乘即进;
(3)无需等到所有结果出来后,将结果转换为字符,可即乘即转。
优化后时间复杂度不变,但节省了空间,代码更简洁。如下:
头文件和数据结构:
#include
#include
#include
#include
#include
using namespace std;
struct bigcheng2
{
string a;
string b;
string result_str;
};
void reverse_data( string &data);//字符串反转
void multiply2(bigcheng2 &tempcheng2);//字符串模拟相乘 字符串反转:
void reverse_data( string &data)
{
char temp = '0';
int start=0;
int end=data.size()-1;
assert( data.size()&& start <= end );
while ( start < end )
{
temp = data[start];
data[start++] = data[end];
data[end--] = temp;
}
}
两数相乘:
void multiply2(bigcheng2 &tempcheng2)
{
reverse_data(tempcheng2.a);//字符串反转
reverse_data(tempcheng2.b);
int c=0;
string temp(tempcheng2.a.size()+tempcheng2.b.size(),'0');//将temp全部初始化为0字符
for (unsigned int i=0;i=0;i--)
{
if (temp[i]!='0')
break;
else
temp.pop_back();
}
reverse_data(temp);//结果?字Á?符¤?串ä?反¤¡ä转Áa
tempcheng2.result_str=temp;
}
主函数:
int main()
{
bigcheng2 tempcheng2;
string a,b;
cin>>a>>b;
tempcheng2.a=a;
tempcheng2.b=b;
multiply2(tempcheng2);
cout<3.2 移位进位法
移位进位法也是普通的大数相乘算法,其时间复杂度也为O(N²)其基本思路参考博客5,简述如下:
按照乘法的计算过程来模拟计算:
1 2
× 3 6
---------- ---- 其中,上标数字为进位数值。
71 2 --- 在这个计算过程中,2×6=12。本位保留2,进位为1.这里是一个简单的计算过程,如果在高位也需要进位的情况下,如何处理?
3 6
-----------
413 2
其代码优化如下:#include
#include
#include
#include
#include
using namespace std;
void reverse_data( string &data);//字符串反转
void compute_value( string lhs,string rhs,string &result );
void reverse_data( string &data)
{
char temp = '0';
int start=0;
int end=data.size()-1;
assert( data.size()&& start <= end );
while ( start < end )
{
temp = data[start];
data[start++] = data[end];
data[end--] = temp;
}
}
void compute_value( string lhs,string rhs,string &result )
{
reverse_data(lhs);
reverse_data(rhs);
int i = 0, j = 0, res_i = 0;
int tmp_i = 0;
int carry = 0;
for ( i = 0; i!=lhs.size(); ++i, ++tmp_i )
{
res_i = tmp_i; //在每次计算时,结果存储的位需要增加
for ( j = 0; j!= rhs.size(); ++j )
{
carry += ( result[res_i] - '0' )+(lhs[i] - '0') * (rhs[j] - '0');//此处注意,每次计算并不能保证以前计算结果的进位都消除, 并且以前的计算结果也需考虑。
result[res_i++] = ( carry % 10 + '0' );
carry /= 10;
}
while (carry)//乘数的一次计算完成,可能存在有的进位没有处理
{
result[res_i++] = (carry % 10 + '0');
carry /= 10;
}
}
for (int i=result.size()-1;i>=0;i--)
{
if (result[i]!='0')
break;
else
result.pop_back();
}
reverse_data(result);
}
int main()
{
string a,b;
cin>>a>>b;
string result(a.size()+b.size(),'0');
compute_value(a,b,result);
cout< 3.3大数相乘优化
3.2 移位进位法中的反转字符串其实不必要的,只需从数组的后面开始计算存储即可,下面实现代码:
char* bigcheng1(char *p1,char *p2)
{
if (check(p1)||check(p2))
throw exception("Invalid input!");
int index1=strlen(p1)-1,index2=strlen(p2)-1,index3,carry=0;
char *p3=new char[index1+index2+3];
memset(p3,'0',index1+index2+2);
p3[index1+index2+2]='\0';
for (;index2>=0;--index2)
{
for (index1=strlen(p1)-1;index1>=0;--index1)
{
int num=p3[index1+index2+1]-'0'+(p1[index1]-'0')*(p2[index2]-'0')+carry;//p3[index1+index2+1]-'0',注意都是数字参与运算
p3[index1+index2+1]=num%10+'0';
carry=num/10;
}
int i=0;
while(carry)
{
p3[index1+index2+1+(i--)]+=(carry%10);//注意字符和字符串的不同
carry/=10;
}
index3=index1+index2+1+i;
}
while(index3>=0)
p3[index3--]='0';
return p3;
}或者下面这样,其实是一样的,下面的相加、相减、相除一样的思路啦
char* bigcheng(char *p1,char *p2)
{
if (check(p1)||check(p2))
throw exception("Invalid input!");
int index1=strlen(p1)-1,index2=strlen(p2)-1,index3,carry=0;
char *p3=new char[index1+index2+3];
memset(p3,'0',index1+index2+2);
p3[index1+index2+2]='\0';
for (;index2>=0;--index2)
{
for (index1=strlen(p1)-1;index1>=0;--index1)
{
int num=p3[index1+index2+1]-'0'+(p1[index1]-'0')*(p2[index2]-'0')+carry;//p3[index1+index2+1]-'0',注意都是数字参与运算
if (num>=10)
{
carry=num/10;
num%=10;
}
else carry=0;
p3[index1+index2+1]=num+'0';
}
int i=0;
while(carry)
{
p3[index1+index2+1+(i--)]+=(carry%10);//注意字符和字符串的不同
carry/=10;
}
index3=index1+index2+1+i;
}
while(index3>=0)
p3[index3--]='0';
return p3;
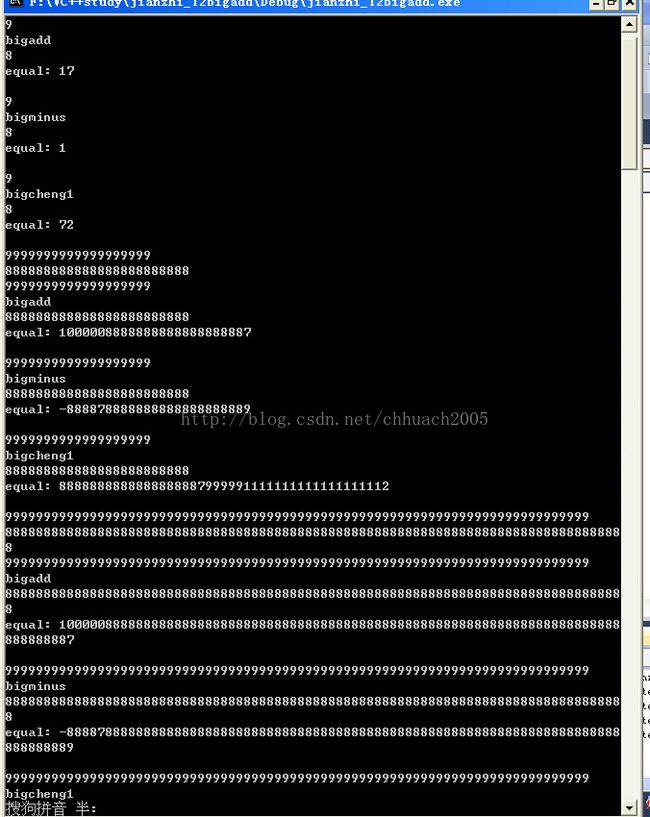
}3.4运行结果
运行结果如图1、图2所示
图1
图2
3.5 大数相加
bool check(char *p)
{
if (!p)
{
return 1;
}
int i=0;
while(p[i]!='\0')
{
if (p[i]<'0'||p[i]>'9')
{
return 1;
}
else ++i;
}
return 0;//合法
}char* bigadd(char *p1,char *p2)
{
if (check(p1)||check(p2))
{
throw exception("Invalid input!");
}
int len1=strlen(p1);
int len2=strlen(p2);
int len3=max(len1,len2)+1;
char *p3=new char[len3+1];
memset(p3,'0',len3);
p3[len3]='\0';
int index1=len1-1,index2=len2-1,index3=len3-1;
int carry=0;
while(index1>=0&&index2>=0)
{
int num=p1[index1--]-'0'+p2[index2--]-'0'+carry;
if (num>=10)
{
carry=1;
num-=10;
}
else
carry=0;
p3[index3--]=num+'0';
}
while(index1>=0)
{
int num=p1[index1--]-'0'+carry;
if (num>=10)
{
carry=1;
num-=10;
}
else
carry=0;
p3[index3--]=num+'0';
}
while(index2>=0)
{
int num=p1[index2--]-'0'+carry;
if (num>=10)
{
carry=1;
num-=10;
}
else
carry=0;
p3[index3--]=num+'0';
}
p3[index3]=carry?'1':'0';
return p3;
}
3.6大数相减
char* bigminus(char *p1,char *p2,bool &flag)
{
if (check(p1)||check(p2))
{
throw exception("Invalid input!");
}
flag=0;//正数默认
if (strlen(p1)=0&&index2>=0)
{
int num=p1[index1--]-p2[index2--]-carry;
if (num<0)
{
carry=1;
num+=10;
}
else carry=0;
p3[index3--]=num+'0';
}
while(index1>=0)
{
int num=p1[index1--]-'0'-carry;
if (num<0)
{
carry=1;
num+=10;
}
else carry=0;
p3[index3--]=num+'0' ;
}
int i=0;
while(p3[i]=='0') ++i;
if (flag)
{
p3[i-1]='-';
}
return p3;
} 3.7大数相除
char* bigchu(char *p1,char *p2)//大数除,有问题,但思想是对的,关键怎么处理前面多样的0
{
bool flag=0;
char *tmp1=new char[strlen(p2)-strlen(p2)+1];
char *tmp0=tmp1,*p3,*p4;
memset(tmp1,'0',strlen(p2)-strlen(p2));
tmp1[strlen(p2)-strlen(p2)]='\0';
char *tmp2=bigminus(p1,p2,flag);
p1=tmp2;
while(!flag)
{
p3=bigadd(tmp0,"1");
tmp1=tmp0;
tmp0=p3;
delete []tmp1;
tmp2=bigminus(p1,p2,flag);
p4=p1;
p1=tmp2;
delete []p4;
}
return tmp0;
}3.8主函数测试
int _tmain(int argc, _TCHAR* argv[])
{
string a,b;
while(1)
{
cin>>a>>b;
char *p1=const_cast(a.c_str());
char *p2=const_cast(b.c_str());
bool flag=0;
char *p3=bigadd(p1,p2);
char *p4=bigminus(p1,p2,flag);
char *p5=bigcheng1(p1,p2);
//char *p6=bigchu(p1,p2);
//cout< 测试结果如下: