扩展的KMP算法图解

扩展的KMP算法，可以在Ο（n + m)的时间复杂度内计算出模板串与文本串的每一个后缀的最长公共前缀，即LCP(T[i:n]，P)。

KMP算法所解决的单模板字符串匹配问题，求得的匹配点是LCP = m的位置，属于该算法的子问题。扩展的KMP算法可以获得更多信息。

定义：文本串长度为n，模板串长度为m

　　　next[i]：模板串P[i:m]和P的最长公共前缀

　　　extend[i]：文本串T[i:n]和P的最长公共前缀（待求）

　　　习惯上使用左闭右开区间，下标从0开始，字符串采用Python的表示法

算法思想：

最大程度利用已匹配的串的信息

算法思路：

假设我们已知了next数组，且当前已知T[p:mx]与P的前缀是匹配的。

设mx表示文本串当前已匹配到的最末位置的下一位置（代比较的位置），p表示与之匹配的模板串与文本串的对齐位置，i表示当前要计算extend值的位置

 比较i+next[i-p]与mx的大小关系，分为两种情况

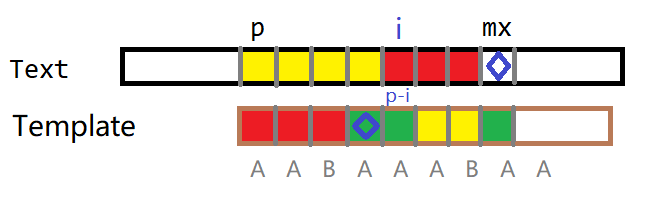
• if (i + next[i - p] < mx)

如图，我们知道p到mx这一段的文本串与模板串是相等的，根据模板串自身的next数组可以知道文本串的extend值至少是next[i - p]，又next数组的定义是“最长”，即确定了下一位不相等。所以extend[i] = next[i - p]

• else

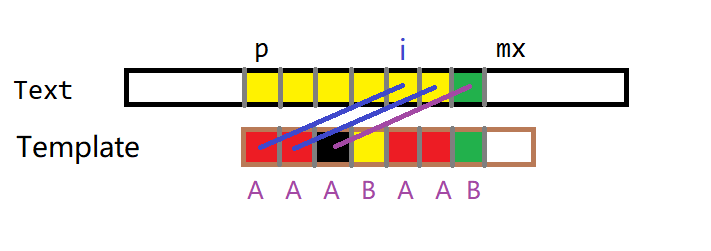
当i + next[i - p] >= mx时，模板串p-i位置的最长公共前缀超出了已知的文本串的范围。我们最大程度地利用已知信息，i位置的extend长度就应当从mx-i开始扩展，接下来比较T[mx]和P[mx - i]（标✦的位置），更新答案和mx、p的值。

匹配算法完毕。接下来我们要考虑模板串的next数组的求法

注意到，　　　next是模板串与模板串的LCP

　　　　　　extend是文本串与模板串的LCP

所以——next的生成其实就是自己对自己套用该算法。我们甚至不需要改变代码，只需令T=P，带入函数即可。

实现细节

#1由于模板串在匹配自身时在初始位置完全相同，要避免mx在一开始就跳到末尾，所以要加个特判，当匹配自身时，要跳过第一位开始比较。

#2当i>=mx时要更新mx的值为i，重返暴力操作

---

 

模板题：洛谷P5410

AC代码：

void exKMP(const char* P, int* nxt, const char* T, int* ext)  P为模板串，nxt是模板串的next数组，T为文本串，ext储存待求的extend值；当ext==nxt时判断为匹配自身，启动特判

 1 #include 
 2 #include <string>
 3 #include 
 4 #include 
 5 using namespace std;
 6 
 7 const int maxn = 1e5 + 1;
 8 int nxtP[maxn], Lcp[maxn];
 9 void exKMP(const char* P, int* nxt, const char* T, int* ext) {
10     int i, mx = 0, p = 0, n = strlen(T), m = strlen(P); //mx: Position where doesn't fit.
11     if (nxt == ext) {
12         ext[0] = n;
13         p = 1; mx = 1; i = 1;
14         while (mx < n && mx - i < m && T[mx] == P[mx - i])    mx++;
15     } else i = 0;
16     
17     for (; i < n; ++i)
18         if (nxt[i - p] + i < mx)    ext[i] = nxt[i - p];
19         else {
20             if (i >= mx)    mx = i; //i >= mx
21             while (mx < n && mx - i < m && T[mx] == P[mx - i])    mx++;
22             ext[i] = mx - i;
23             p = i;
24         }
25     return;
26 }
27 signed main() {
28     string T, P;
29     cin>>T>>P;
30     exKMP(P.data(), nxtP, P.data(), nxtP);
31     exKMP(P.data(), nxtP, T.data(), Lcp);
32     copy(nxtP, nxtP + P.length(), ostream_iterator <int> (cout, " "));
33     cout<<endl;
34     copy(Lcp, Lcp + T.length(), ostream_iterator <int> (cout, " "));
35     return 0;
36 }

View Code