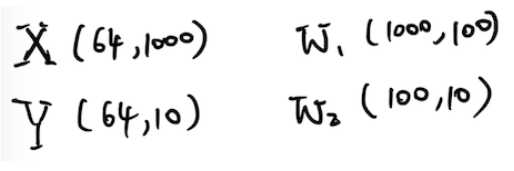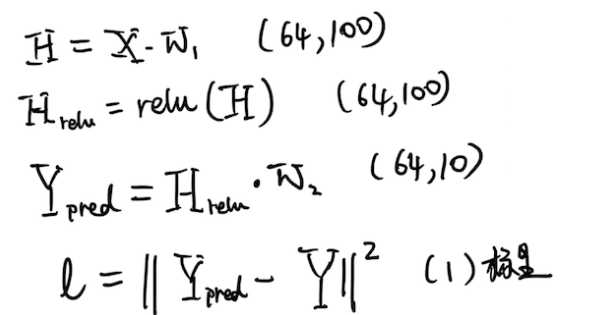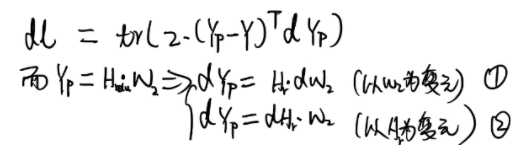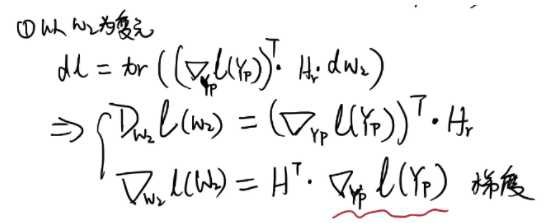[神经网络]反向传播梯度计算数学原理
1 文章概述
本文通过一段来自于Pytorch官方的warm-up的例子:使用numpy来实现一个简单的神经网络。使用基本的数学原理,对其计算过程进行理论推导,以揭示这几句神奇的代码后面所包含的原理。
估计对大多数的同学来说,看完这个文章,肯定会是这样的感觉:字都认识,但是就是不知道讲的是啥~!不过对于有心人来说,本文确实能起到点睛之笔,就是你研究很久后,还差一点火候就顿悟了,希望本文能够帮你顿悟。
关键字:Numpy,神经网络,矩阵分析,反射传播,梯度下降
如果发现图片裂了,请左转至 其它平台查看:
https://zhuanlan.zhihu.com/p/32368246
2 实现代码
numpy作为一个科学计算库,并不包含:计算图,尝试学习,梯度等等功能,但是我们可以简单的通过numpy去拟合一个二层的网络。
解决的问题:
- 随机生成一组输入数据,一组输出数据。
- 定义一个神经网络结构及其参数
- 根据输入数据正向传播,求出误差
- 根据误差反向传播梯度,更新神经元的各个节点的参数
代码如下:
# -*- coding: utf-8 -*-
import numpy as np
# N is batch size; D_in is input dimension;
# H is hidden dimension; D_out is output dimension.
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random input and output data
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
# Randomly initialize weights
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
learning_rate = 1e-6
for t in range(500):
# Forward pass: compute predicted y
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
# Compute and print loss
loss = np.square(y_pred - y).sum()
print(t, loss)
# Backprop to compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
# Update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
原文见:Learning PyTorch with Examples
3 网络结构
将上面的代码结构及相应的参数维度绘图后如下所示:
然后本代码使用的是一个大小为64的batch,所以输入的值实际的大小实际上是(64,1000)。
把以上的代码转化成数学公式如下,括号里面是相应的矩阵的形状:
4 正向计算
数据流的正向传播
最后计算出损失函数loss,是实际预测值和先验数据矩阵的二范数,作为两组矩阵的距离测度。
正向传播比较简单,基本上大学的线性代数的基本知识看几章,就能很好的理解。这也是后续如果在深度学习框架下面设计网络的时候,注意设计神经元大小的时候,需要考虑矩阵乘法的可行性,即维度相容。
PS:关于矩阵的范数的定义,详情见P32的《1.4.3矩阵的内积和范数》
5 反向传播
5.1 实现代码
下面是反射传播的代码实现:
5.2 数学基础
关于反射传播的数学原理,可能就不是那么好理解了,因为这里面需要用到矩阵的高级算法,一般的理工科数学的《线性代数》甚至《高等代数》里面都没有提到相关的内容,所以基本上已经超过了大多数高校学生的知识范围了。在这个时候,就要祭出张贤达的《矩阵分析》了。
最开始我把自己大学时候的数学书《数学分析》,《高等代数》,《数值计算》都翻了一遍,但是都没有找到相关的内容。感觉对于矩阵的微分是一个“三不管”的地带,但是这个内容又是深度学习神经网络中用得最多的数学原理。然后到网上发现了《矩阵分析与应用》,想想这么厚的一本像百科全书的书,应该是无所不包吧,果然在里面找到了想要的内容。
当然在看书之前,也看了无数的网络文章,相对比较有价值的就下面两篇:
《矩阵求导-上》https://zhuanlan.zhihu.com/p/24709748
《矩阵求导-下》https://zhuanlan.zhihu.com/p/24863977
当然,像数学工具这种内容,建议大家还是去看书,因为书作为几十年的经典教材,其推导过程,内容的完整性,认证的严密性都是经得起推敲的。网络文章只能帮大家启蒙一下,学几个术语,但是具体想深入了解细节,建议还是看书。
言归正传。
上述的不到10行的反向传播梯度,更新参数的代码,在外行人看来是比较神来之笔,完全摸不着头脑,这是很正常的。因为要理解上述的代码,需要预先储备如下知识(《矩阵分析与应用》):
- 矩阵的基本运算。页面P4,章节编号1.1.2
- 矩阵的内积与范数。P32, 1.4.3
- 矩阵的迹。P49, 1.6.4
- 向量化和矩阵化。 P74, 1.11
- Jacobian矩阵和梯度矩阵。 P143, 3.1
- 一阶实矩阵微分与Jacobian矩阵辨识。 P152, 3.2
注意事项:函数有不同的分类,所以请大家不要全用《线性代数》里面变元全为实数标量的眼光来看待矩阵的变元和矩阵函数的运算。因为它们是不同的,即使你勉强得到符合代码的结论,那很可能也是“瞎猫碰到死耗子”。关于函数的微分的讨论,光实值函数的分类,就可以分如下几类(P143, 3.1):
矩阵和Jacobian矩阵在实值区间内是互为转置。在进行数学推导时,都是先根据Jacobian矩阵的辨识方法求出Jacobian矩阵,然后转置后就是相应的梯度。
当定义一个标量函数关于变量的偏导数时:
Jacobian矩阵和梯度矩阵是关于偏导的不同定义方式,分别是行向量偏导和列向量偏导。只是Jacobian矩阵是一种研究思维上更自然的选择,但是梯度向量却是优化和实际工程计算时更自然的选择。
5.3 预测值梯度
grad_y_pred = 2.0 * (y_pred - y)
下面是推导过程,红色笔迹是推导过程的依据,请查阅《矩阵分析与应用》
接着前面的公式,继续求微分:
5.4 参数W2梯度
grad_w2 = h_relu.T.dot(grad_y_pred)
5.5 参数H_relu 梯度
grad_h_relu = grad_y_pred.dot(w2.T)
5.6 Relu梯度
grad_h = grad_h_relu.copy() grad_h[h < 0] = 0 grad_w1 = x.T.dot(grad_h)
5.7 参数W1梯度
然后后面就是使用梯度和学习率去批量更新参数,实现整个训练过程了。
6 参考资料
《矩阵分析与应用》(第2版) 张贤达 著,清华大学出版社,2011-11,第2版
本文中所有的引用注解,页面标识都来自于本书。