在两个字符串中,有些字符会一样,可以形成的子序列也有可能相等,因此,长度最长的相等子序列便是两者间的最长公共字序列,其长度可以使用动态规划来求。
以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。
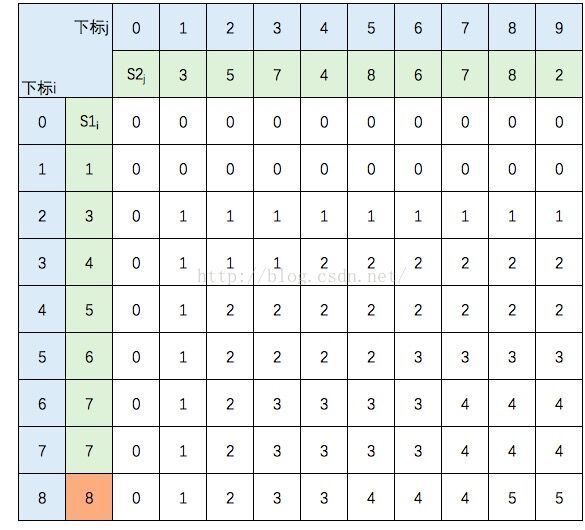
借用《算法导论》中的推导图:
创建 DP数组C[][];
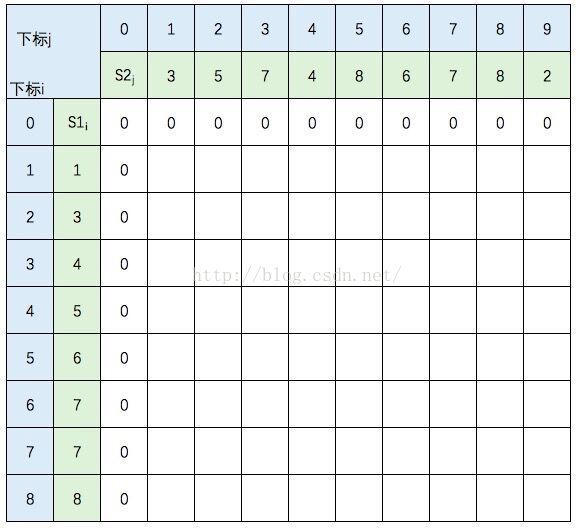
图中的空白格子需要填上相应的数字(这个数字就是c[i][j]的定义,记录的LCS的长度值)。填的规则依据递归公式,简单来说:如果横竖(i,j)对应的两个元素相等,该格子的值 = c[i-1,j-1] + 1。如果不等,取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表:
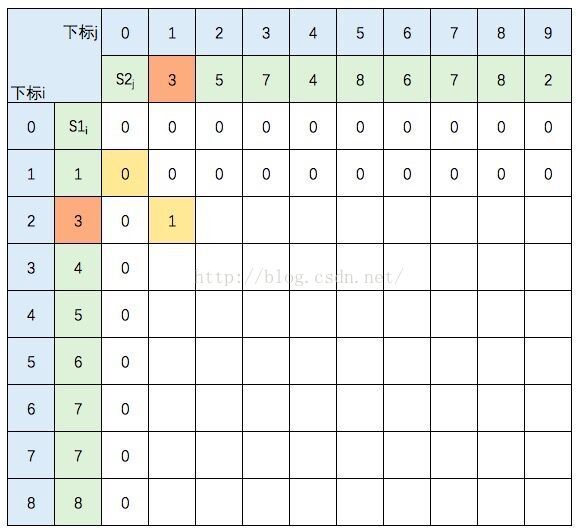
然后,一行一行地从上往下填:
S1的元素3 与 S2的元素3 相等,所以 c[2,1] = c[1,0] + 1。继续填充:
S1的元素3 与 S2的元素5 不等,c[2,2] =max(c[1,2],c[2,1]),图中c[1,2] 和 c[2,1] 背景色为浅黄色。
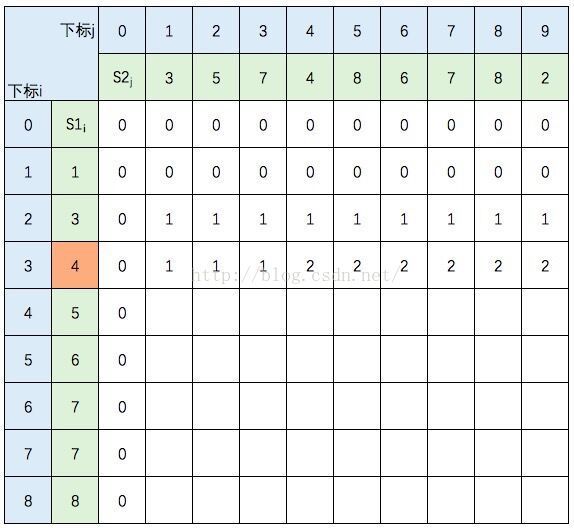
继续填充:
中间几行填写规则不变,直接跳到最后一行:
至此,该表填完。根据性质,c[8,9] = S1 和 S2 的 LCS的长度,即为5。
得到公式
代码
#include
#include
#include
#include
using namespace std;
const int MAXN = 1005;
int DP[MAXN][MAXN];
int main()
{
string a;
string b;
while(cin >> a >> b)
{
int l1 = a.size();
int l2 = b.size();
memset(DP, 0, sizeof(DP));
for(int i = 1; i <= l1; i++)
for(int j = 1; j <= l2; j++)
if(a[i - 1] == b[j - 1])
DP[i][j] = max(DP[i][j], DP[i - 1][j - 1] + 1);
else
DP[i][j] = max(DP[i][j - 1], DP[i - 1][j]);
printf("%d\n", DP[l1][l2]);
}
return 0;
}
当得到完整的DP表之后,我们可以通过倒推来得到相应的子序列
S1和S2的最LCS并不是只有1个,本文并不是着重讲输出两个序列的所有LCS,只是介绍如何通过上表,输出其中一个LCS。
我们根据递归公式构建了上表,我们将从最后一个元素c[8][9]倒推出S1和S2的LCS。
c[8][9] = 5,且S1[8] != S2[9],所以倒推回去,c[8][9]的值来源于c[8][8]的值(因为c[8][8] > c[7][9])。
c[8][8] = 5, 且S1[8] = S2[8], 所以倒推回去,c[8][8]的值来源于 c[7][7]。
以此类推,如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,这里请都选择一个方向(之后遇到这样的情况,也选择相同的方向)。
第一种结果为:
这就是倒推回去的路径,棕色方格为相等元素,即LCS = {3,4,6,7,8},这是其中一个结果。
如果如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,选择另一个方向,会得到另一个结果。
即LCS ={3,5,7,7,8}。
在倒推时,如果s1[i] == s2[j] 就跳转到c[i - 1][j - 1],如果s1[i] != s1[j], 就向前找或向上找(只能一个方向)
PS:在代码中和解说中代码细节有所不同,在解说图中s从下标1开始,在代码中从下标0开始。
---------------------
作者:someone_and_anyone
来源:CSDN
原文:https://blog.csdn.net/someone_and_anyone/article/details/81044153