Copyright © Microsoft Corporation. All rights reserved.
适用于License版权许可
更多微软人工智能学习资源,请见微软人工智能教育与学习共建社区
- Content
- 01.0-神经网络的基本工作原理
- 01.1-基本数学导数公式
- 01.2-Python-Numpy库的点滴
- 02.0-反向传播与梯度下降
- 02.1-线性反向传播
- 02.2-非线性反向传播
- 02.3-梯度下降
- 03.0-损失函数
- 03.1-均方差损失函数
- 03.2-交叉熵损失函数
- 04.0-单入单出单层-单变量线性回归
- 04.1-最小二乘法
- 04.2-梯度下降法
- 04.3-神经网络法
- 04.4-梯度下降的三种形式
- 04.5-实现逻辑非门
- 05.0-多入单出单层-多变量线性回归
- 05.1-正规方程法
- 05.2-神经网络法
- 05.3-样本特征数据的归一化
- 05.4-归一化的后遗症
- 05.5-正确的推理方法
- 05.6-归一化标签值
- 06.0-多入多出单层神经网络-多变量线性分类
- 06.1-二分类原理
- 06.2-线性二分类实现
- 06.3-线性二分类结果可视化
- 06.4-多分类原理
- 06.5-线性多分类实现
- 06.6-线性多分类结果可视化
- 07.0-激活函数
- 07.1-挤压型激活函数
- 07.2-半线性激活函数
- 07.3-用双曲正切函数分类
- 07.4-实现逻辑与门和或门
- 08.0-单入单出双层-万能近似定理
- 08.1-双层拟合网络的原理
- 08.2-双层拟合网络的实现
- 09.0-多入多出双层-双变量非线性分类
- 09.1-实现逻辑异或门
- 09.2-理解二分类的工作原理
- 09.3-非线性多分类
- 09.4-理解多分类的工作原理
- 10.0-调参与优化
- 10.1-权重矩阵初始化
- 10.2-参数调优
- 10.3-搜索最优学习率
- 10.4-梯度下降优化算法
- 10.5-自适应学习率算法
- 11.0-深度学习基础
- 11.1-三层神经网络的实现
- 11.2-验证与测试
- 11.3-梯度检查
- 11.4-手工测试训练效果
- 11.5-搭建深度神经网络框架
- 12.0-卷积神经网络
- 12.1-卷积
- 12.2-池化
- 14.1-神经网络模型概述
- 14.2-Windows模型的部署
- 14.3-Android模型的部署
知识点
- 多元线性回归
- 输入层的矩阵运算设计
- 样本数据归一化
提出问题
假设有如下这样一个问题:有1000个样本,每个样本有三个特征值,一个标签值。想让你预测一下给定任意三个特征值组合,其y值是多少?
| 样本序号 | 1 | 2 | 3 | 4 | ... | 1000 |
|---|---|---|---|---|---|---|
| 样本特征值1 | 1 | 4 | 2 | 4 | ... | 2 |
| 样本特征值2 | 3 | 2 | 6 | 3 | ... | 3 |
| 样本特征值3 | 96 | 100 | 54 | 72 | ... | 69 |
| 样本标签值y | 434 | 500 | 321 | 482 | ... | 410 |
这就是典型的多元线性回归。函数模型如下:
\[y=a_0+a_1x_1+a_2x_2+\dots+a_kx_k\]
为了方便大家理解,咱们具体化一下上面的公式,按照本系列文章的符号约定就是:
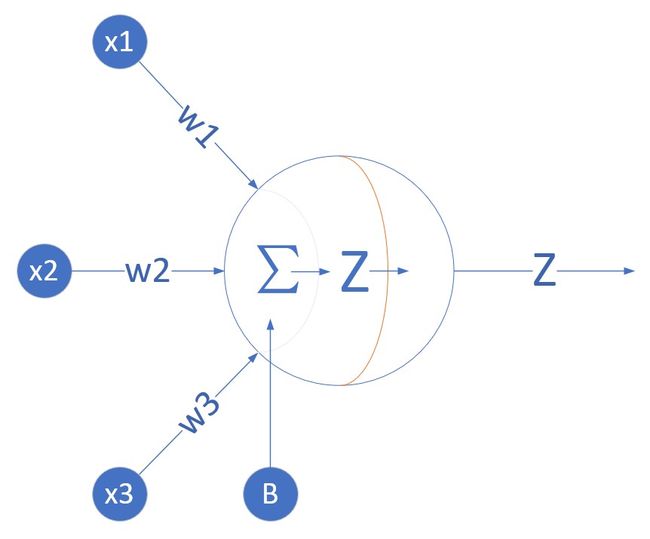
\[ Z = w_1x_1+w_2x_2+w_3x_3+b = WX + B \]
定义神经网络结构
我们定义一个一层的神经网络,输入层为3或者更多,反正大于2了就没区别。这个一层的神经网络没有中间层,只有输出层,而且只有一个神经元,并且神经元有一个线性输出,不经过激活函数处理。亦即在下图中,经过\(\Sigma\)求和得到Z值之后,直接把Z值输出。
这样的一个神经网络能做什么事情呢?
输入层
假设一共有m个样本,每个样本n个特征值,X就是一个\(n \times m\)的矩阵,模样是这样紫的(n=3,m=1000,亦即3行1000列):
\[ X = \begin{pmatrix} x1_1 & x2_1 & \dots & xm_1 \\ \\ x1_2 & x2_2 & \dots & xm_2 \\ \\ x1_3 & x2_3 & \dots & xm_3 \end{pmatrix} = \begin{pmatrix} 3 & 2 & \dots & 3 \\ \\ 1 & 4 & \dots & 2 \\ \\ 96 & 100 & \dots & 54 \end{pmatrix} \]
\[ Y = \begin{pmatrix} y1 & y2 & \dots & ym \\ \end{pmatrix}= \begin{pmatrix} 434 & 500 & \dots & 410 \\ \end{pmatrix} \]
单独看一个样本是这样的:
\[ x1 = \begin{pmatrix} x1_1 \\ \\ x1_2 \\ \\ x1_3 \end{pmatrix} = \begin{pmatrix} 3 \\ \\ 1 \\ \\ 96 \end{pmatrix} \]
\[ y1 = \begin{pmatrix} 434 \end{pmatrix} \]
\(x1\)表示第一个样本,\(x1_1\)表示第一个样本的一个特征值。
权重W和B
有人问了,为何不把这个表格转一下,变成横向是样本特征值,纵向是样本数量?那样好像更符合思维习惯?
确实是!但是在实际的矩阵运算时,由于是\(Z=W*X+B\),W在前面,X在后面,所以必须是这个样子的:
\[ \begin{pmatrix} w1 & w2 & w3 \end{pmatrix} \times \begin{pmatrix} x1_1 \\ \\ x1_2 \\ \\ x1_3 \end{pmatrix}+B= w1*x1_1+w2*x1_2+w3*x1_3+B \]
假设每个样本X有n个特征向量,上式中的W就是一个\(1 \times n\)行向量,让每个w都对应一个x:
\[ \begin{pmatrix}w_1 & w_2 \dots w_n\end{pmatrix} \]
B是个单值,因为只有一个神经元,所以只有一个bias,每个神经元对应一个bias,如果有多个神经元,它们都会有各自的b值。
输出层
由于我们只想完成一个回归(拟合)任务,所以输出层只有一个神经元。由于是线性的,所以没有用激活函数。
收集训练数据
房价预测问题,成为了机器学习的一个入门话题。我们也不能免俗,但是,不要用美国的什么多少平方英尺,多少个房间的例子来说事儿了,中国人不能理解。我们来个北京的例子!
影响北京房价的因素有很多,几个最重要的因子和它们的取值范围是:
- 朝向(在北方地区,窗户面向阳光的房子要抢手一些):北=1,西=2,东=3,南=4
- 地理位置:二环,三环,四环,五环,六环,分别取值为2,3,4,5,6,二环的房子单价最贵
- 面积:40~120平米,连续值
由于一些原因,收集的数据不能用于教学,所以咱们根据以上规则创造一些数据:
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
# y = w1*x1 + w2*x2 + w3*x3 + b
# W1 = 朝向:1,2,3,4 = N,W,E,S
# W2 = 位置几环:2,3,4,5,6
# W3 = 面积:平米
def TargetFunction(x1,x2,x3):
w1,w2,w3,b = 2,10,5,10
return w1*x1 + w2*(10-x2) + w3*x3 + b
def CheckFileData():
Xfile = Path("HouseXData.npy")
Yfile = Path("HouseYData.npy")
if Xfile.exists() & Yfile.exists():
XData = np.load(Xfile)
YData = np.load(Yfile)
return True,XData,YData
return False,None,None
def create_sample_data(m):
flag,XData,YData = CheckFileData()
if flag == False:
X0 = np.random.randint(1,5,m)
X1 = np.random.randint(2,7,m)
X2 = np.random.randint(40,120,m)
XData = np.zeros((3,m))
XData[0] = X0
XData[1] = X1
XData[2] = X2
Y = TargetFunction(X0,X1,X2)
noise = 20
Noise = np.random.randint(1,noise,(1,m)) - noise/2
YData = Y.reshape(1,m)
np.save("HouseXData.npy", XData)
np.save("HouseYData.npy", YData)
return XData, YData在TargetFunction函数中,\(w2*(10-x2)\),是因为越靠近二环的房子越贵,所以当x2=2时(二环),10-2=8;当x2=6时(六环),10-6=4。
令w1=2, w2=10, w3=5, b=10,所以最后的公式是:
\[z = w1·x_1 + w2·(10-x_2)+w3·x_3+b \\ = 2x_1 - 10(10-x_2)+5x_3+10 \\ = 2x_1 - 10x_2+5x_3+110 \]
定义前向计算过程
def forward_calculation(Xm,W,b):
z = np.dot(W, Xm) + b
return 定义代价函数
我们用传统的均方差函数: \(loss = \frac{1}{2}(Z-Y)^2\),其中,Z是每一次迭代的预测输出,Y是样本标签数据。我们使用所有样本参与训练,因此损失函数实际为:
\[Loss = \frac{1}{2}(Z - Y) ^ 2\]
其中的分母中有个2,实际上是想在求导数时把这个2约掉,没有什么原则上的区别。
def check_diff(w, b, X, Y, count, prev_loss):
Z = w * X + b
LOSS = (Z - Y)**2
loss = LOSS.sum()/count/2
diff_loss = abs(loss - prev_loss)
return loss, diff_loss求针对W和B的梯度函数
求解W和B的梯度方法与我们前面的文章“单入单出的一层神经网络”完全一样,所以不再赘述,只说一下结论:
因为:
\[z = wx+b\]
\[loss = \frac{1}{2}(z-y)^2\]
所以我们用loss的值作为基准,去求w对它的影响,也就是loss对w的偏导数:
\[ \frac{\partial{loss}}{\partial{w}} = \frac{\partial{loss}}{\partial{z}}*\frac{\partial{z}}{\partial{w}} = (z-y)x \]
\[ \frac{\partial{loss}}{\partial{b}} = \frac{\partial{loss}}{\partial{z}}*\frac{\partial{z}}{\partial{b}} = z-y \]
变成代码:
def dJwb_single(Xm,Y,Z):
dloss_z = Z - Y
db = dloss_z
dw = np.dot(dloss_z, Xm.T)
return dw, db每次迭代后更新W,B的值
def update_weights(w, b, dw, db, eta):
w = w - eta*dw
b = b - eta*db
return w,b主程序初始化
m = 1000 # 创造1000个样本
XData, Y = create_sample_data(m)
X = XData
n = X.shape[0] # 每个样本的特征数
eta = 0.1 # 学习率0.1
loss, diff_loss, prev_loss = 10, 10, 5
eps = 1e-10
max_iteration = 100 # 最多100次循环
# 初始化w,b
b = np.zeros((1,1))
w = np.zeros((1,n))程序主循环
for iteration in range(max_iteration):
for i in range(m):
Xm = X[0:n,i].reshape(n,1)
Ym = Y[0,i].reshape(1,1)
Z = forward_calculation(Xm, W, B)
dw, db = dJwb_single(Xm, Ym, Z)
W, B = update_weights(W, B, dw, db, eta)
loss, diff_loss = check_diff(w,b,xxx,y,1,prev_loss)
if diff_loss < eps:
print(i)
break
prev_loss = loss
print(iteration, w, b, diff_loss)
if diff_loss < eps:
break怀着期待的心情用颤抖的右手按下了运行键......but......what happened?
C:\Users\Python\LinearRegression\MultipleInputSingleOutput.py:61: RuntimeWarning: overflow encountered in square
LOSS = (Z - Y)**2
C:\Users\Python\LinearRegression\MultipleInputSingleOutput.py:63: RuntimeWarning: invalid value encountered in double_scalars
diff_loss = abs(loss - prev_loss)
C:\Users\Python\LinearRegression\MultipleInputSingleOutput.py:55: RuntimeWarning: invalid value encountered in subtract
w = w - eta*dw
0 [[nan nan nan]] [[nan]] nan
1 [[nan nan nan]] [[nan]] nan
2 [[nan nan nan]] [[nan]] nan
3 [[nan nan nan]] [[nan]] nan怎么会overflow呢?于是右手的颤抖没有停止,左手也开始颤抖了。
我们遇到了传说中的梯度爆炸!数值太大,导致计算溢出了。第一次遇到这个情况,但相信不会是最后一次,因为这种情况在神经网络中太常见了。技术只服务于相信技术的人,技能只给与培养技能的人!别慌,让我们debug一下。
解决梯度爆炸
检查迭代中的数值变化情况
先把迭代中的关键值打印出来:
0 -----------
Z: [[0.]]
Y: [[469]]
dLoss/dZ: [[-469.]]
dw: [[ -938. -1876. -37051.]]
db: [[-469.]]
W: [[ 93.8 187.6 3705.1]]
B: [[46.9]]
1 -----------
Z: [[289982.7]]
Y: [[464]]
dLoss/dZ: [[289518.7]]
dw: [[ 579037.4 1158074.8 22582458.60000001]]
db: [[289518.7]]
W: [[ -57809.94 -115619.88 -2254540.76]]
B: [[-28904.97]]
2 -----------
Z: [[-2.62364972e+08]]
Y: [[634]]
dLoss/dZ: [[-2.62365606e+08]]
dw: [[-5.24731213e+08 -1.57419364e+09 -3.04344103e+10]]
db: [[-2.62365606e+08]]
W: [[5.24153113e+07 1.57303744e+08 3.04118649e+09]]
B: [[26207655.65900001]]
......最开始的W,B的值都是0,三次迭代后,W,B的值已经大的超乎想象了。可以停止运行程序了,想一想为什么。
难道是因为学习率太大吗?目前是0.1,设置成0.01试试看:
0 ----------
Z: [[0.]]
Y: [[469]]
dLoss/dZ: [[-469.]]
dw: [[ -938. -1876. -37051.]]
db: [[-469.]]
W: [[ 0.938 1.876 37.051]]
B: [[0.469]]
1 -----------
Z: [[2899.827]]
Y: [[464]]
dLoss/dZ: [[2435.827]]
dw: [[ 4871.654 9743.308 189994.506]]
db: [[2435.827]]
W: [[ -3.933654 -7.867308 -152.943506]]
B: [[-1.966827]]
2 ----------
Z: [[-17798.484679]]
Y: [[634]]
dLoss/dZ: [[-18432.484679]]
dw: [[ -36864.969358 -110594.908074 -2138168.222764]]
db: [[-18432.484679]]
W: [[ 32.93131536 102.72760007 1985.22471676]]
B: [[16.46565768]]没啥改进。
回想一个问题:为什么在“单入淡出的一层神经网络”一文的代码中,我们没有遇到这种情况?因为所有的X值都是在[0,1]之间的,而神经网络是以样本在事件中的统计分布概率为基础进行训练和预测的,也就是说,样本的各个特征的度量单位要相同。我们并没有办法去比较1米和1公斤的区别,但是,如果我们知道了1米在整个样本中的大小比例,以及1公斤在整个样本中的大小比例,比如一个处于0.2的比例位置,另一个处于0.3的比例位置,就可以说这个样本的1米比1公斤要小。这就提出了样本的归一化或者正则化的理论。
数据归一化
更多的数据归一化的问题,我们会另文给出,下面只提对我们解决当前问题有用的方法。
min-max标准化
也叫离差标准化,是对原始数据的线性变换,使结果落到[0,1]区间,转换函数如下:
\[ x_{new} = \frac{x-x_{min}}{x_{max}-x_{min}} \]
其中max为样本数据的最大值,min为样本数据的最小值。
如果想要将数据映射到[-1,1],则将公式换成:
\[ x_{new} = \frac{x-x_{mean}}{x_{max}-x_{min}} \]
mean表示数据的均值。
样本分析
再把这个表拿出来分析一下:
| 样本序号 | 1 | 2 | 3 | 4 | ... | 1000 |
|---|---|---|---|---|---|---|
| 样本特征值1:窗户朝向 | 1 | 3 | 2 | 4 | ... | 2 |
| 样本特征值2:地理位置 | 3 | 2 | 6 | 3 | ... | 4 |
| 样本特征值3:居住面积 | 96 | 100 | 54 | 72 | ... | 69 |
| 样本标签值y:房价(万元) | 434 | 500 | 321 | 482 | ... | 410 |
特征值1 - 窗户朝向
一共有”东”“南”“西”“北“四个值,用数字化表示是:
东:3
南:4
西:2
北:1
因为超南的房子比较贵,其次为东,西,北。为啥东比西贵?因为夏天时朝西的窗户西晒时间长,比较热。特征值2 - 地理位置
二环:2 - 单价最贵
三环:3
四环:4
五环:5
六环:6 - 单价最便宜特征值3 - 房屋面积
统计所有样本数据得到房屋的面积范围是[40,120]
我们用min-max标准化来归一以上数据,得到下表:
| 样本序号 | 1 | 2 | 3 | 4 | ... | 1000 |
|---|---|---|---|---|---|---|
| 样本特征值1:窗户朝向 | 0 | 0.667 | 0.333 | 1 | ... | 0.33 |
| 样本特征值2:地理位置 | 0.25 | 0 | 1 | 0.25 | ... | 0.75 |
| 样本特征值3:居住面积 | 0.7 | 0.75 | 0.175 | 0.4 | ... | 0.36 |
| 样本标签值y:房价(万元) | 434 | 500 | 321 | 482 | ... | 410 |
还有一个问题:标签值y是否需要归一化?没有任何理论说需要归一化标签值,所以我们先把这个问题放一放。
数据归一化的好处
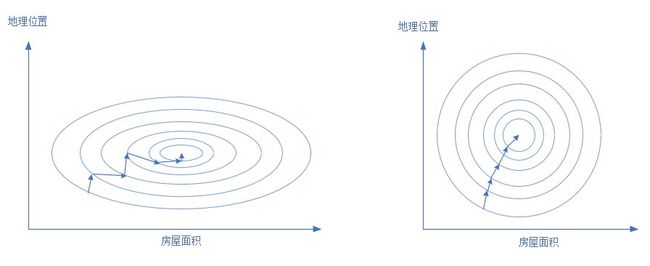
下图展示了归一化前后的情况,左侧为前,右侧为后:
房屋面积的取值范围是[40,120],而地理位置的取值范围是[2,6],二者会形成一个很扁的椭圆,如左侧。这样在寻找最优解的时候,过程会非常曲折。运气不好的话,如同我们上面的代码,根本就没法训练。
归一化后,地理位置和房屋面积二者都归一到[0,1]之间,变成了可比的了,而且寻找最优解的路径也很直接,节省了时间。
归一化的实现
我们把归一化的函数写好:
def Normalize(X):
X_new = np.zeros(X.shape)
n = X.shape[0]
w_num = np.zeros((1,n))
for i in range(n):
v = X[i,:]
max = np.max(v)
min = np.min(v)
w_num[0,i] = max - min
v = (v - min)/(max-min)
X_new[i,:] = v
return X_new, w_num然后再改一下主程序,加上归一化的调用:
m = 1000
XData, Y = create_sample_data(m)
X, W_num = Normalize(XData)
n = X.shape[0]
eta = 0.1
loss, diff_loss, prev_loss = 10, 10, 5
eps = 1e-10
max_iteration = 1
B = np.zeros((1,1))
W = np.zeros((1,n))
for iteration in range(max_iteration):
for i in range(m):
Xm = X[0:n,i].reshape(n,1)
Ym = Y[0,i].reshape(1,1)
Z = forward_calculation(Xm, W, B)
dw, db = dJwb_single(Xm, Ym, Z)
W, B = update_weights(W, B, dw, db, eta)
loss, diff_loss = check_diff(W,B,Xm,Ym,1,prev_loss)
if diff_loss < eps:
print(i)
break
prev_loss = loss
print(iteration, W, B, diff_loss)
if diff_loss < eps:
break用颤抖的双手同时按下Ctrl+F5,运行开始,结束,一眨眼!仔细看打印结果:
[[ 5.94417016 -40.05847929 394.83396979]] [[292.15951172]]\[ w1=5.94417016 \\ w2=-40.05847929 \\ w3=394.83396979 \\ b=292.15951172 \]
比较一下原始公式:
\[z = w1·x_1 + w2·(10-x_2)+w3·x_3+b \\ = 2x_1 - 10(10-x_2)+5x_3+10 \\ = 2x_1 - 10x_2+5x_3+110 \\ w1=2 \\ w2=-10 \\ w3=5 \\ b=110 \]
什么鬼!怎么相差这么多?!
归一化的后遗症
仔细想想,训练居然收敛了,出结果了,但是和我们预期的不太一致。我们没有做归一化前,根本没结果。归一化后有结果,那么就是归一化起作用了,但它有什么副作用呢?一起逐个分析一下4个值。
w1是窗户朝向,取值范围[1,4],即:\(x_{min}=1, x_{max}=4\),目前\(w1=5.94417\),试着变换一下:
\[ \frac{w1}{x_{max}-x_{min}} = \frac{5.94417}{4-1}=1.98139 \simeq 2 \]
是不是和w1=2这个值非常的接近呢?!WoW!我从澡盆里跳了出来,给阿基米德打了一个电话,说:“我找到啦!”
再看W2是地理位置:
\[ \frac{w2}{x_{max}-x_{min}} = \frac{-40.058}{6-2}=-10.0145 \simeq -10 \]
再看W3是房屋面积:
\[ \frac{w3}{x_{max}-x_{min}} = \frac{394.8339}{119-40}=4.997 \simeq 5 \]
代码如下:
W_rel = np.zeros((1,n))
for i in range(n):
W_rel[0,i] = W[0,i] / W_num[0,i]
print(W_rel)其中W_num是在调用Normalize函数时返回的三个特征值的范围,亦即(3,4,79)。
再看b值......"元芳,你怎么看?"
“卑职以为,b值不是样本值,没有经过归一化。”
“你说得很对!但我们怎么解出b呢?”
“大人,这个好办,我们如此这样这样......把一堆样本值代入w1,w2,w3的公式,令b=0,看看计算出来的结果是什么,再和样本标签值去比较就可以了!”
\[ z = w1*x_1+w2*x_2+w3*x_3 +0\\ b = y - z \]
为了避免单个的样本误差,用100个样本做比较,得到差值之和,再平均,代码如下:
B = 0
for i in range(10):
xm = XData[0:n,i].reshape(n,1)
zm = forward_calculation(xm, W_rel, 0)
ym = Y[0,i].reshape(1,1)
B = B + (ym - zm)
b = B / 10
print(b)我们在计算z的时候,故意把第三个参数设置为0,即令b=0。ym是每个样本的标签值,它与z的差值自然就是真正的b值。
上述两段代码得到的输出如下:
[[ 1.98139005 -10.01461982 4.99789835]]
[[110.29389945]]至此,我们完美地解决了北京地区的房价预测问题!但是还没有解决自己可以有能力买一套北京的房子的问题......
最后遗留一个问题,如果标签值y也归一化的话,也可以得到训练结果,但是怎么解释呢?大家有兴趣的话可以研究一下,分享出来。反正笔者是没研究出来。
点击这里提交问题与建议
联系我们: [email protected]
学习了这么多,还没过瘾怎么办?欢迎加入“微软 AI 应用开发实战交流群”,跟大家一起畅谈AI,答疑解惑。扫描下方二维码,回复“申请入群”,即刻邀请你入群。