DoG算子和LoG算子

DoG(Difference of Gaussian)算子和LoG(Laplacian of Gaussian)算子是常用的极值点检测(Blob Detection)两种方法，高斯卷积是为了进行尺度变换，那么LapLacian呢。 因此这里首先引入LapLacian算子。

图像边缘检测

因此进行边缘检测有两种方法。

1. 一阶导数的极值

梯度算子定义为：$G(x,y)=\sqrt{{\nabla }_{x}f(x,y{)}^2+{\nabla }_{y}f\left(x,y^2\right)}$

为了简化计算，一般梯度算子可以写为:
$G(x,y)=\left|{\nabla }_{x}f(x,y)\right|+\left|{\nabla }_{y}f(x,y)\right|$

于是得到的一阶算子有检测对角线边缘的罗伯特算子:
$R(x,y)=\max \{|f(x,y)-f(x+1,y+1)|,|f(i+1,j)-f(i-1,j+1)|\}$

对应卷积模板为:
$\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$

$\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

加了高斯平滑的边缘检测算子
$S(x,y)=|f(x+1,y-1)+2\ast f(x+1,y)+f(x+1,y+1)-f(x-1,y-1)-2\ast f(x-1,y)-f(x-1,y+1)|+|f(x+1,y+1)+2\cdot f(x,y+1)+f(x-1,y+1)-f(x+1,y-1)-2\cdot f(x,y-1)-f(x-1,y-1)|$

对应的卷积模板为
$\left[\begin{array}{ccc}1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right]$
$\left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]$

2. 二阶导数的过零点

二阶导数算子实际就是Laplace算子，定义为两个方向一阶导数的内积，符号表示$\Delta$
$\Delta ={\nabla }^2=\left[\frac{\partial }{\partial x}\frac{\partial }{\partial y}\right]{\left[\frac{\partial }{\partial x}\frac{\partial }{\partial y}\right]}^T=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$

使用二阶差分代替二阶函数，则
$\begin{array}{rl}\Delta f(x,y)& ={\Delta }_{x}f(x,y)+{\Delta }_{y}f(x,y)\\ & =f(x+1,y)-f(x,y)-f(x,y)+f(x-1,y)\\ & +f(x,y+1)-f(x,y)-f(x,y)+f(x,y-1)\\ & =f(x-1,y-1)+f(x-1,y+1)+f(x+1,y-1)+f(x+1,y+1)-4f(x,y)\end{array}$
那么卷积模板为：
$\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$

如果考虑四个方向：
$\Delta f(x,y)={\Delta }_{x}f(x,y)+{\Delta }_{y}f(x,y)+{\Delta }_{zy}f(x,y)+{\Delta }_{yx}f(x,y)$
那么卷积模板为
$\left[\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}\right]$

由于Laplace算子对噪声很敏感，所以一般利用高通滤波器进行平滑处理，所以引入了高斯拉普拉斯算子(LoG,Laplacian of Gaussian)

高斯拉普拉斯算子(LoG, Laplacian of Gaussian)

对于图像$I(x,y)$，首先通过尺度为$\sigma$的高斯平滑
$G_{\sigma }(x,y)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{x^2+y^2}{2{\sigma }^2}\right)$

在使用Laplace算子检测边缘
$\Delta |G_{\sigma }(x,y)\ast I(x,y)]=\left[\Delta G_{\sigma }(x,y)\right]\ast I(x,y)$

该式证明如下：
$\begin{array}{rl}\frac{d}{d{t}^2}[h(t)\ast f(t)]& =\frac{d}{dt}\int f(\tau )h(t-\tau )d\tau \\ & =\int f(\tau )\frac{d}{d{t}^2}h(t-\tau )d\tau =f(t)\ast \frac{d}{d{t}^2}h(t)\end{array}$
所以高斯拉普拉斯算子等价于先对高斯函数求二阶导，再与原图进行卷积

将高斯拉普拉斯算子展开：
$LoG=\Delta G_{\sigma }(x,y)=\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial x^2}+\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial y^2}=\frac{x^2+y^2-2{\sigma }^2}{{\sigma }^4}{e}^{-\left(x^2+y^2\right)/2{\sigma }^2}$

高斯函数差分(DoG, Difference of Gaussian of Gaussian)

DoG即对不同尺度下的高斯函数的差分，DoG算子表达如下:
$DoG=G_{{\sigma }_1}-G_{{\sigma }_2}=\frac{1}{\sqrt{2\pi }}\left[\frac{1}{{\sigma }_1}{e}^{-\left(x^2+y^2\right)/2{\sigma }_1^2}-\frac{1}{{\sigma }_2}{e}^{-\left(x^2+y^2\right)/2{\sigma }_2^2}\right]$

由于归一化的LoG算子：
$\begin{array}{rl}{L}_{\text{ norm }}& ={\sigma }^2\left(G_{xx}(x,y,\sigma )+G_{yy}(x,y,\sigma )\right)\\ & =\sigma \frac{\partial G}{\partial \sigma }\end{array}$

而$\frac{\partial G}{\partial \sigma }\approx \frac{G(x,y,k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$

所以: $G(x,y,k\sigma )-G(x,y,\sigma )\approx (k-1){\sigma }^2{\nabla }^{2}G$

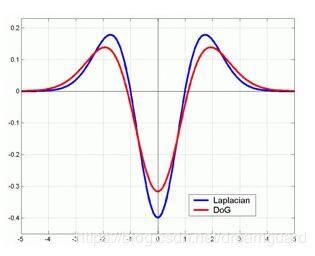
即DoG算子和LoG算子具有类似的波形，仅仅是幅度不同，不影响极值点的检测，而DoG算子的计算复杂度显然低于LoG，因此一般使用DoG代替LoG算子

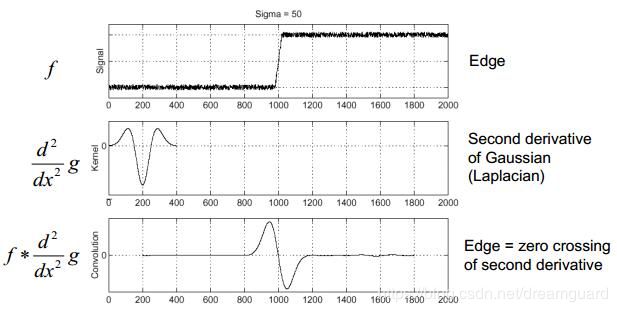
利用DoG或LoG进行边缘和极值点检测

边缘检测：图像边缘在LoG算子下的响应情况如下图所示，二阶微分算子在边缘处为一过零点(由于图像是离散的，也可能不是零点附近)，而且过零点两边的最大值(正)和最小值(负)的差值较大。

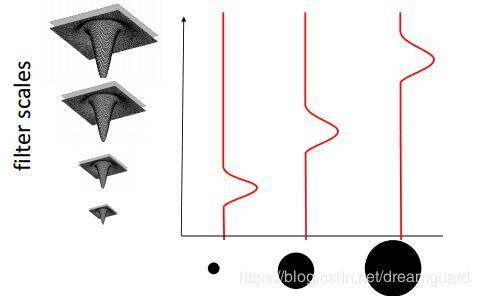
极值点检测：随着矩形宽度的减小，响应变化如下。

通过不同尺度的高斯滤波器，可以检测不同大小的Blob。这里解释一下斑点通常和关键点(keypoint)，兴趣点(intrestpoint)以及特征点(featurepoint)表示同一个概念，通常指与周围有着颜色和灰度区别的区域。

https://senitco.github.io/2017/06/20/image-feature-LoG-DoG/
https://www.cnblogs.com/YiXiaoZhou/p/5891645.html