KMP算法解析

KMP是一个经典的字符串匹配算法，同时也是目前效率最高匹配算法之一。当遇到“寻找子串”这类问题时，都可以参考一下KMP的思想，说不定会有意外收获哟。KMP的设计很精妙，但美中不足的是难以理解。所以趁着自己脑袋瓜还比较清楚的时候，赶紧都记录下来。

 

首先，我们从一个朴素的问题开始引导。就是经典的字符串匹配问题。

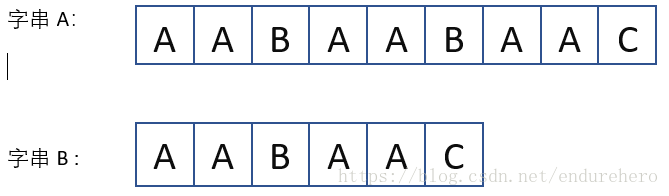
问题：目前有2个字符串，字串A 和字串B。判断字串B是否是字串A的子串。为了更好的聚焦算法，设定A.length() > B.length()。举个栗子：

看到这种问题的第一反应，也就是最朴素的想法莫过于暴力搜素（当然暴力无脑破解往往效率都是最低的）。如下图所示：

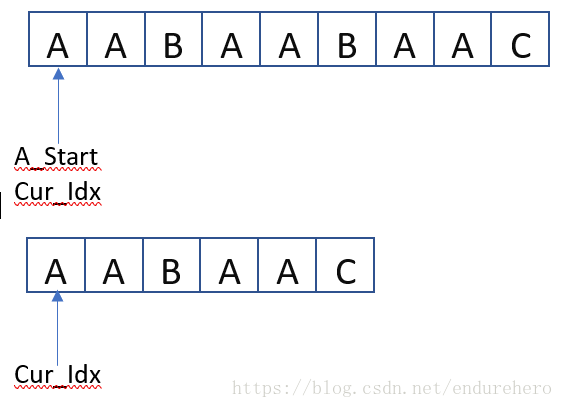
A_Start: 表示A中候选子串的起始位置；Cur_Idx：表示当前需要判断的字符位置；（索引均为0-base）;

当A[A_Start + Cur_Idx] == B[Cur_idx]时，将Cur_idx向前移动，直到出现以下2种情况之一时停止:

1. Cur_Idx已到达B串末尾，说明B是A的子串，并且B在A中的起始位置为A_Start;
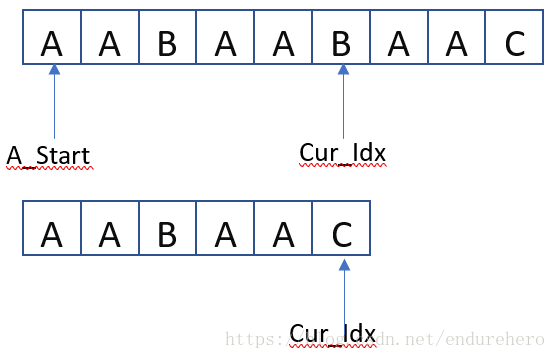
2. A[A_Start + Cur_Idx] != B[Cur_idx]。B串和A中的当前候选子串不匹配。如下图所示：

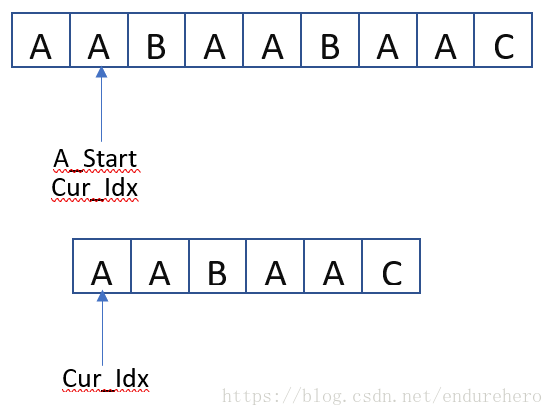
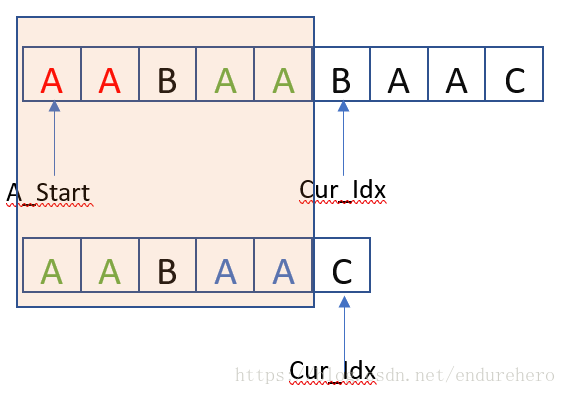
当出现第2种情况时，需要将Cur_Idx重置到B串的起始位置，并将A_Start向前移动一位，重复上文中的步骤对A中新的候选子串进行搜索。如下图所示：

以上就是暴力搜索的思想，简单、易用、好理解，但是似乎效率并不高。KMP相对于暴力搜索的改进是充分利用已匹配字串所获得的信息，使得每次发生字符不匹配时（也即上文中的第2种情况），A_Start不再是一位一位的往前移，Cur_Idx 也不是每次都要回到B串的起始位置。下面开始介绍KMP的解法。我们将场景复盘到一次出现字符不匹配的情况，如下图所示：

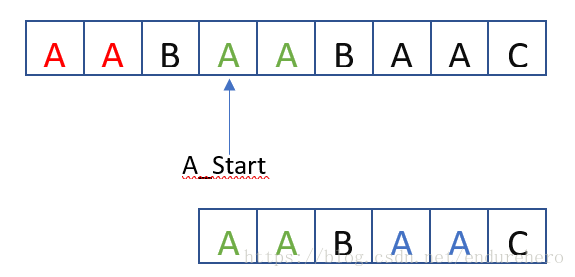
经过之前的步骤后，我们发现蓝色方框内的部分是完全匹配的。同时还可以观察到一个信息，就是字串B的前2个绿色A字符和最后的2个蓝色A字符是重复的。而字串B中的蓝色A字符和字串A中的绿色A字符是匹配的。那么A_Start是否可以直接移动到字串A的第一个绿色A字符处呢？如下图所示：

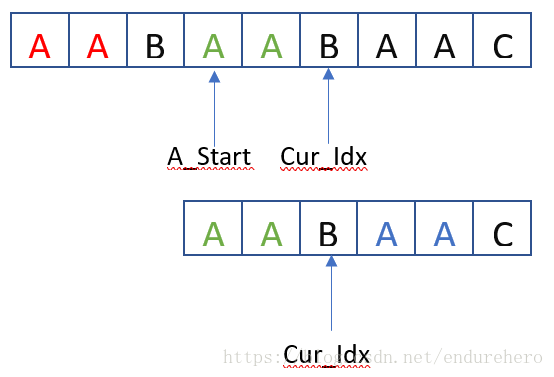
对于字串B而言，由于仅仅知道前2个绿色A字符和字串A是匹配的，而第3个字符B的匹配情况还位置，因此，需要将Cur_Idx移动到第3个字符B处。如下图所示：

这样就减小A_Start和Cur_Idx的移动次数，提高了搜索效率。

为了实现上面所介绍的效果，KMP采用next表来存储字串B内的重复信息。这里涉及到了前缀和后缀的概念。前缀是指以字符串的第一个字符开始的一段连续的字符序列，但该序列中不会包含字符串的最后一个字符；后缀则是以非字符串第一个字符开头到最后一个字符的一个连续序列。

举个栗子，字串abcdabcd；

其前缀为a, ab, abc, abcd, abcda, abcdab, abcdabc；

其后缀为d, cd, bcd, abcd, dabcd, cdabcd, bcdabcd;

next表的长度和字符串的长度相同，其中每一位存储了到这一位为止的子串中最大相同前缀和后缀的长度。还是以abcdabcd举例，这个字符串的长度是8，所以next是一个8位的数组next[8];因此，next[0] 统计的是子串a的最大相同前缀后缀长度，next[1]统计的是子串ab的最大相同前缀后缀长度，next[2]统计的是子串abc的最大相同前缀后缀长度，以此类推。那么最大相同前缀后缀的长度怎么计算呢。我们以next[7]举例，也即统计子串abcdabcd（字串本身也是自己的子串啦）的最大相同前缀后缀。

这个字串的前缀有a, ab, abc, abcd, abcda, abcdab, abcdabc

这个字串的后缀有d, cd, bcd, abcd, dabcd, cdabcd, bcdabcd

所以最大的相同前缀后缀是abcd, 也即next[7] = 4，我们按照同样的方法计算next表中的其他成员，最终会得到：

Idx	0	1	2	3	4	5	6	7
val	0	0	0	0	1	2	3	4
substr	a	ab	abc	abcd	abcda	abcdab	abcdabc	abcdabcd

 

为了更好的应用next表中的信息，我们将next表中每个元素的语义设定为如果当前字符匹配但下一个字符不匹配，那么当前索引需要跳转的位置，则该表的值将变为：

Idx	0	1	2	3	4	5	6	7
val	-1	-1	-1	-1	0	1	2	3
substr	a	ab	abc	abcd	abcda	abcdab	abcdabc	abcdabcd

我们用C++来实现next表的制作过程：

void makeNext(const string& B, vector& next)
{
	next[0] = -1;
	for(int i = 1, k = -1; i < B.length(); ++i)
	{
		while(k > -1 && B[i] != B[k+1]) k = next[k];
		
		if(B[k+1] == B[i]) next[i] = ++k;
		else next[i] = k;
	}
}

有了next表之后，下一个问题是next表该怎么用呢？还记得上文中描述的KMP和暴力搜索之间的区别吗？我们就用next表来实现当出现字符不匹配时，A_Start 和Cur_Idx的移动。代码如下所示：

int KMP(const string& A, const string& B) {
        if(B.empty()) return 0;
        int A_len = A.length(), B_len = B.length();

        if(A_len < B_len) return -1;
	
        vector next(B_len, -1);
        makeNext(B, next);
        
        for(int A_Start = 0, Cur_Idx = -1; A_Start+Cur_Idx+1 < A_len;)
        {
            if(A[A_Start + Cur_Idx + 1] == B[Cur_Idx+1])
            {
                ++Cur_Idx;
                if(Cur_Idx == B_len - 1) return A_Start;
            }
            else if(-1 != Cur_Idx)
            {
                A_Start += (Cur_Idx - next[Cur_Idx]);
                Cur_Idx = next[Cur_Idx];
            }
            else
            {
                A_Start++;
            }
                
        }

        return -1;
    }

当然还有一种更加精简的实现方法，如下：

int KMP(const string& A, const string& B) {
        if(B.empty()) return 0;
        int A_len = A.length(), B_len = B.length();

        if(A_len < B_len) return -1;
        
        vector next(B_len, -1);
        makeNext(B, next);
        
        for(int A_Start = 0, Cur_Idx = -1; A_Start < A_len; ++A_Start)
        {
            while(Cur_Idx > - 1 && A[A_Start] != B[Cur_Idx + 1]) Cur_Idx = next[Cur_Idx];
            if(A[A_Start] == B[Cur_Idx + 1])
            {
                ++Cur_Idx;
                 If(Cur_Idx == B_len - 1) return Cur_Idx – B_len + 1;
            }
                
        }

        return -1;
    }