【360】2019秋招笔试题（圈地运动、Bitttts、魔法阵列）python

笔试已挂，诸位随意看看就好，笔者编程水平一般。


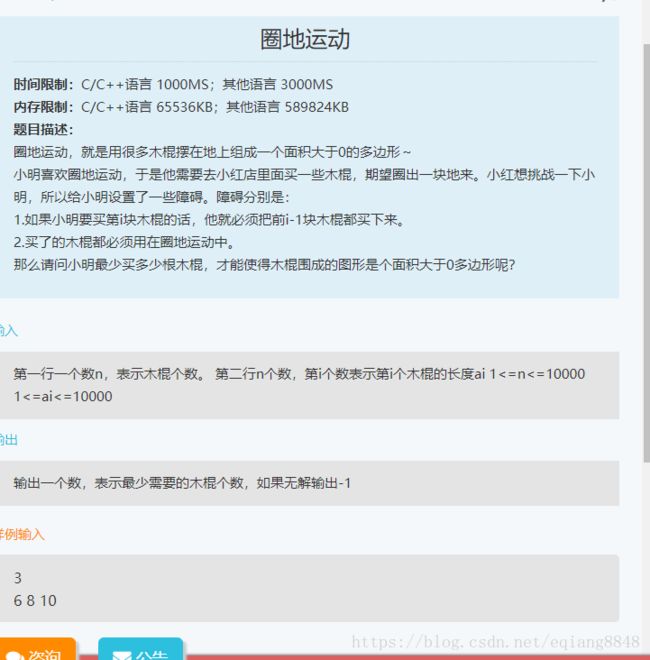
木棍数n<3，不会组成多边形；n>=3，只要判断前n-1个的长度和是否比最大的那个大，大就说明能组成多边形。

n = int(raw_input())
stem = map(int,raw_input().split())

def duobianxing(seq):
    seq.sort()
    if sum(seq[:-1])>seq[-1]:
        return True

if n<3:
    print -1
else:
    flag = True
    for i in range(3,len(stem)+1):
        if duobianxing(stem[:i]):
            print i
            flag = False
            break

    if flag:
        print -1

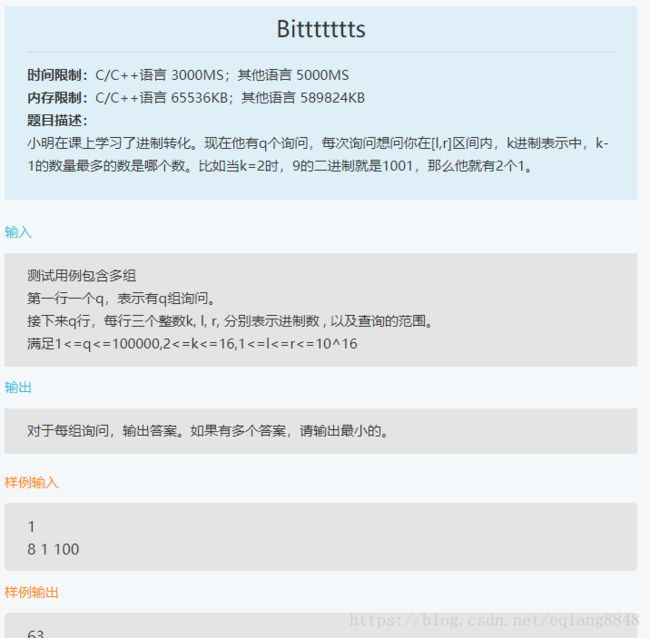
这题有意思，先举个例子，2进制的1数量最多的数分别是 1, 11, 111，规律是11=10+1,111=100+10+1（这里意会成十进制加了），三位数100加上之前二位数、一位数的最大值，八进制7, 70, 700，7,77,777这样。所以就是判断有几位数的7（8进制的话）。首先确定位数，math.log(r,k)，比如8进制，r=100,那么8^2=64，所以int(math.log(l,k))=2。
此例下，n2=2，所以while循环后z=7+70 = 77(八进制下的77),(7:7*8^0 ；70: 7*8^1)，但是我们只判断了上界，什么时候需要判断下界限呢，就是比如l=64，r=100，比如l从64开始取，这样是不会取到63的。要如何把下界也引入呢？分别把上下界带入（上下界作为上界），如果返回1样的数字就是0，不一样就是返回上界的答案。

import math
def pp(l,r,k):
    
    if l<=0 or r<=0 or k<=0 or l>r:
        return -1
    n1=int(math.log(l,k))
    n2=int(math.log(r,k))
    z=0
    n=0
    #print(n1,n2)
    def cc(n2,n,k,z):
        while n<=n2-1:
            z+=(k**n)*(k-1)
            if z<r:
                n+=1
            else:
                break
                #return z-(k**n)*(k-1)
           # n=n-1
            g=0
            z=0
            while g<=n-1:
                z+=(k**g)*(k-1)
                g+=1
        return z
    if cc(n1,n,k,z)==cc(n2,n,k,z) :
        return 0
    else:
        return cc(n2,n,k,z)

t = int(input())

while t:
    t-=1
    k,l,r = [int(i) for i in input().split()]
    print(pp(l,r,k))

这题贴一个同学写的代码，过了9%

import java.util.Scanner;

/**
 * Created by Zhaoyang Ge on 2018/9/17.
 */
public class 魔法排列 {
    public static int getResult(int n, int[] a) {

        int[] arr = new int[n];
        for (int i = 1; i <= n; i++) {
            arr[i - 1] = i;
        }
        int[] res = {0};
        process(arr, 0, a,res);  //全排列
        return res[0];
    }


    private static void process(int[] arr, int i, int[] a,int[] res) {
//        int res = 0;
        if (i == arr.length) {
            for (int j = 1; j < arr.length; j++) {

                res[0] += Math.abs(a[arr[j] - 1] - a[arr[j - 1] -1 ]);
            }
        }
        for (int j = i; j < arr.length; j++) {
            swap(arr, i, j);
            process(arr, i + 1, a, res);   //交换位置
            swap(arr, i, j);
        }

    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }


    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int len = sc.nextInt();
        int[] arr = new int[len];
        for (int i=0; i < len; i++){
            arr[i] = sc.nextInt();
        }
        System.out.println(getResult(len,arr));
    }
}