分冶—递归 更有效的算法方法(棋盘覆盖,分段区间,循环赛事日程表,最大最小值 )
文章的开头就不废话了,直接开门见山了
分冶-递归,文章的开头那几个经典题目,有做过的朋友应该很有感触吧,没做过的朋友请自行百度,谢谢!
个人感觉,分冶-递归,首先讨论范围,不管是大范围还是小范围,其实解题思路,解题方案是一样一样的,就连函数的接口,出口都是一样的,最典型的就是循环赛事问题和棋盘覆盖问题
先由简单的循环赛事问题入手
问题描述:
设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;(2)每个选手一天只能参赛一次;
(3)循环赛在n-1天内结束。
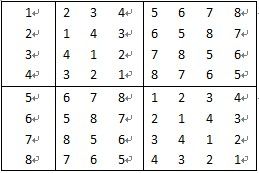
请按此要求将比赛日程表设计成有n行和n-1列的一个表。在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n,1≤j≤n-1。8个选手的比赛日程表如下图:
代码如下:
#include
using namespace std;
int a[90][90];
/*
x表示当前的格子左上角的行数
y代表当前的格子右上角的列数
k代表当前的格子边长
*/
void K_list(int x, int y, int k){
int kk, j;
if(k == 1)
return;
kk = k/2;
//覆盖左上角
K_list(x, y, k/2);
//覆盖右上角
K_list(x, y+kk, k/2);
//覆盖左下角
for(j = 0; j < kk; j++){
a[x+kk][y+j] = a[x][y+j] + kk;
}
K_list(x+kk, y, k/2);
//覆盖右下角
for(j = 0; j < kk; j++){
a[x+kk][y+j+kk] = a[x][y+kk+j] - kk;
}
K_list(x+kk, y+kk, k/2);
}
int main(){
int i = 1, ii = 1;
for(i; i <= 8; i++){
a[1][i] = i;
}
K_list(1,1,8);
for(i = 1; i <= 8; i++){
for(ii = 1; ii <= 8; ii++){
cout<
cout<
return 0;
}
分析:看到覆盖左上角和覆盖右上角的,就只有一个递归调用函数,而覆盖左下角和右下角,在递归之前还加了个for循环,因为我在文章一开头就说过,不管是小范围还是大范围,接口和出口还是思路都是一样一样的,2*2的表格分成4个左上,右上,左下,右下小范围,左下的值等于左上的值加上边的一半,即2/2=1,而右下的值等于右上的值减去边的一半,再把2*2回归到4*4的表格,其实也是一样的,可以自己好好想想,再分析为何左上和右上2个递归函数前面没有for,因为之前我就在a【1】【i】,即第一行赋予初值,已经有值,为何在赋予新值呢?所以,不管进去N*N是左上还是左下,还是右上,还是右下的范围内,第一行,其实就在递归到最底层的时候已经赋予了初值,所以万变不离其宗,其实就是那句话,不管大小范围,都是一样一样的!
棋盘覆盖问题
问题描述:
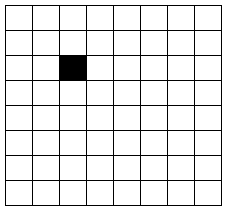
在一个2^k×2^k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何k≥0,有4^k种不同的特殊棋盘.
下图–图(1)中的特殊棋盘是当k=3时16个特殊棋盘中的一个:
图(1)
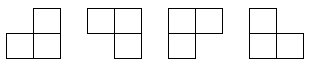
题目要求在棋盘覆盖问题中,要用下图-图(2)所示的4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖.
图(2)
题目包含多组测试数据,输入包含测试数据组数N,下面输入N组数据,每组数据,包括边长m和特殊方格的位置x,y。
input sample
2
2
0 0
8
2 2
output sample
CASE:1
0 1
1 1
CASE:2
3 3 4 4 8 8 9 9
3 2 2 4 8 7 7 9
5 2 0 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
代码如下(这是网上copy代码,因为楼主代码在实验室,但这题的代码都是差不多):
#include
#include
using namespace std;
const int N = 11;
int Board[N][N];
int tile = 0;
/*
tr:棋盘左上角方格的行号
tc:棋盘左上角方格的列号
dr:特殊方格所在的行号
dc:特殊方格所在的列号
size:方形棋盘的边长
*/
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
if(size == 1)
return;
int t = ++tile, s = size/2;
//覆盖左上角子棋盘
if(dr
ChessBoard(tr, tc, dr, dc, s);
else // 此棋盘无特殊方格
{
// 用t号L型骨型牌覆盖右下角
Board[tr+s-1][tc+s-1] = t;
// 覆盖其余方格
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
}
//覆盖右上角子棋盘
if(dr
ChessBoard(tr, tc+s, dr, dc, s);
else
{
Board[tr+s-1][tc+s] = t;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
}
//覆盖左下角子棋盘
if(dr>=tr+s && dc
else
{
Board[tr+s][tc+s-1] = t;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
}
//覆盖右下角子棋盘
if(dr>=tr+s && dc>=tc+s)
ChessBoard(tr+s, tc+s, dr, dc, s);
else
{
Board[tr+s][tc+s] = t;
ChessBoard(tr+s, tc+s, tr+s, tc+s, s);
}
}
void DisplayBoard(int size)
{
for(int i=1; i<=size; ++i)
{
for(int j=1; j<=size; ++j)
printf("%2d ", Board[i][j]);
printf("\n");
}
}
int main()
{
ChessBoard(1, 1, 1, 1, 4);
DisplayBoard(4);
return 0;
}
先写这2个,下次有时间再写