李航 统计学习方法 第一章 课后 习题 答案

1.1

统计学习方法的三要素是模型、策略、算法。

伯努利模型是定义在取值为0与1的随机变量上的概率分布。

统计学分为两派：经典统计学派和贝叶斯统计学派。两者的不同主要是，经典统计学派认为模型已定，参数未知，参数是固定的，只是还不知道；贝叶斯统计学派是通过观察到的现象对概率分布中的主观认定不断进行修正。

极大似然估计和贝叶斯估计的模型都是伯努利模型也就是条件概率模型；极大似然估计用的是经典统计学派的策略，贝叶斯估计用的是贝叶斯统计学派的策略；为了得到使经验风险最小的参数值，使用的算法都是对经验风险求导，使导数为0.

定义随机变量A为一次伯努利试验的结果，A的取值为 {0,1} { 0 , 1 } ，概率分布为 P(A) P ( A ) ：

P(A=1)=θP(A=0)=1−θ P ( A = 1 ) = θ P ( A = 0 ) = 1 − θ

下面分布用极大似然估计和贝叶斯估计来估计 θ θ 的值。

极大似然估计：

L(θ)=∏i=1nP(Ai)=θk(1−θ)n−k L ( θ ) = ∏ i = 1 n P ( A i ) = θ k ( 1 − θ ) n − k

Ai A i 代表第i次随机试验。

θ=argmaxθL(θ)=kn θ = a r g max θ L ( θ ) = k n

贝叶斯估计：

P(θ|A1,A2,...,An)=P(A1,A2,...An|θ)π(θ)P(A1,A2,...,An) P ( θ | A 1 , A 2 , . . . , A n ) = P ( A 1 , A 2 , . . . A n | θ ) π ( θ ) P ( A 1 , A 2 , . . . , A n )

根据观察到的结果修正 θ θ ，也就是假设 θ θ 是随机变量， θ θ 服从 β β 分布，有很多个可能的取值，我们要取的值时在已知观察结果的条件下使 θ θ 出现概率最大的值。上式分母是不变的，求分子最大就可以。

θ=argmaxθP(A1,A2,...An|θ)P(θ)=argmaxθ∏i=1nP(Ai|θ)P(θ)=argmaxθθk(1−θ)n−kθa−1(1−θ)b−1=k+(a−1)n+(a−1)+(b−1) θ = a r g max θ P ( A 1 , A 2 , . . . A n | θ ) P ( θ ) = a r g max θ ∏ i = 1 n P ( A i | θ ) P ( θ ) = a r g max θ θ k ( 1 − θ ) n − k θ a − 1 ( 1 − θ ) b − 1 = k + ( a − 1 ) n + ( a − 1 ) + ( b − 1 )

其中 a,b a , b 是 β β 分布中的参数 β(θ;a,b)=θa−1(1−θ)b−1一个常数 β ( θ ; a , b ) = θ a − 1 ( 1 − θ ) b − 1 一 个 常 数 ，选定 a,b a , b 后就可以确定 θ θ 。如 选择a=b=2，则θ=k+1n+2 选 择 a = b = 2 ， 则 θ = k + 1 n + 2 。 （a,b怎么选最合理，我不知道。） （ a , b 怎 么 选 最 合 理 ， 我 不 知 道 。 ）
如果错误，欢迎指正。
参考：

http://blog.csdn.net/a358463121/article/details/52562940
http://blog.csdn.net/guohecang/article/details/52313046
http://www.math.zju.edu.cn/webpagenew/UploadFiles/AttachFiles/2010421221717128.pdf
https://guangchun.wordpress.com/2011/10/13/ml-bayes-map/
http://www.guokr.com/question/547339/
http://blog.csdn.net/guohecang/article/details/52313046

---

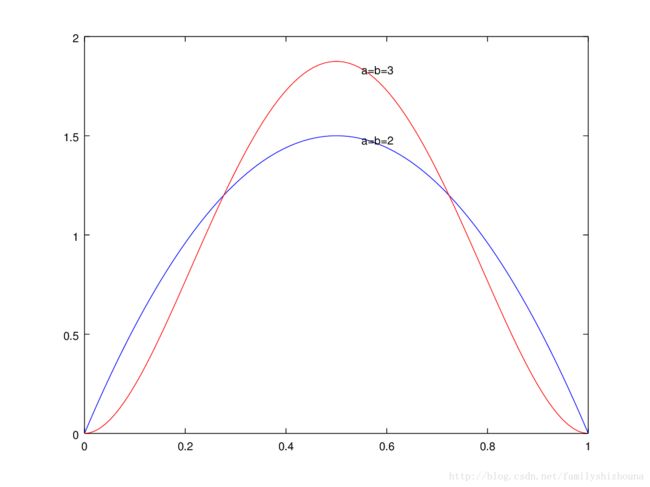
下图是 β β 分布： β(θ;a,b)=θa−1(1−θ)b−1一个常数 β ( θ ; a , b ) = θ a − 1 ( 1 − θ ) b − 1 一 个 常 数

1.2

模型是条件概率分布： Pθ(Y|X) P θ ( Y | X ) ，
损失函数是对数损失函数： L(Y,P(Y|X))=−logP(Y|X) L ( Y , P ( Y | X ) ) = − l o g P ( Y | X ) ，
经验风险为：

Remp(f)=1N∑i=1NL(yi,f(xi))=1N∑i=1N−logP(yi|xi)=−1N∑i=1NlogP(yi|xi) R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) = 1 N ∑ i = 1 N − l o g P ( y i | x i ) = − 1 N ∑ i = 1 N l o g P ( y i | x i )

最小化经验风险，也就是最大化 ∑Ni=1logP(yi|xi) ∑ i = 1 N l o g P ( y i | x i ) ，也就是最大化 ∏Ni=1P(yi|xi) ∏ i = 1 N P ( y i | x i ) ，这个就是极大似然估计。