李航 统计学习方法 第五章 决策树 课后 习题 答案

决策树是一种基本的分类和回归方法。决策树呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间和类空间上的条件概率分布。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。决策树学习通常包括三个步骤：特征选择、决策树的生成和决策树的剪枝。（ID3、C4.5、CART）

1 特征选择

特征选择在于选取对训练数据具有分类能力的特征。通常特征选择的准则是信息增益或信息增益比。

1.1 熵（entropy）

熵是表示随机变量不确定性的度量。 X 是一个取有限个值的离散随机变量，其概率分布为

P(X=xi)=pi,i=1,2,…,n

则随机变量 X 的熵定义为

H(X)=−∑i=1npi log pi

熵越大，随机变量的不确定性就越大。

1.2 条件熵

设有随机变量 (X,Y) ，其联合概率分布为

P(X=xi,Y=yi)=pij,i=1,2,…,n;j=1,2,…,m

条件熵 H(Y|X) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。

H(Y|X)=∑i=1n piH(Y|X=xi)

这里， pi=P(X=xi), i=1,2,…,n.

1.3 信息增益

信息增益：特征 A 对训练数据集 D 的信息增益 g(D,A) ，定义为集合 D 的经验熵 H(D) 与特征 A 给定条件下 D 的经验条件熵 H(D|A) 之差，即

g(D,A)=H(D)−H(D|A)

1.4 信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。（取值较多的特征，可以这样理解，这个特征取值特别多，每条实例一个值，如果选择这个特征，那么每个分支都只有一条实例，也就是每个分支都属于同一个类，这个分支的熵就是0，这个特征的条件熵也就是0。这对其他的特征是不公平的，所以将信息增益除于这个特征的熵）

信息增益比：特征 A 对训练数据集 D 的信息增益比 gR(D,A) 定义为其信息增益 g(D,A) 与训练数据集 D 关于特征 A 的值的熵 HA(D) 之比，即

gR(D,A)=g(D,A)HA(D)

其中， HA(D)=−∑ni=1|Di||D|log2|Di||D| ， n 是特征 A 取值的个数。

2 决策树的生成

2.1 ID3 算法

ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。

2.2 C4.5 算法

C4.5用信息增益比来选择特征

3 决策树的剪枝

决策树的剪枝往往通过极小化决策树整体的损失函数来实现。设树 T 的叶节点个数为 |T| ， t 是树 T 的叶节点，该叶节点有 Nt 个样本点，其中 k 类的样本点有 Ntk 个， k=1,2,…,K ， Ht(T) 为叶节点 t 上的经验熵， α≥0 为参数，则决策树学习的损失函数可以定义为

Cα(T)=∑t=1|T|NtHt(T)+α|T|

其中经验熵为

Ht(T)=−∑kNtkNtlogNtkNt

用 动态规划实现剪枝算法。

c4.5和id3生成算法源码：
https://github.com/zhouna/ml_python/tree/master/decisionTree

4 CART 算法

classification and regression tree, CART 分类与回归树，假设决策树是二叉树。
决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。

5 习题解答

5.1 根据表5.1所给的训练数据集，利用信息增益比（C4.5算法）生成决策树。

输入： A1={1,2,3},A2={1,2},A3={1,2},A4={1,2,3}
输出： C={0,1}

其中 Ai,i=1,2,3,4 分别代表年龄，有工作，有自己的房子，信贷情况； C 代表类别。 A1 的取值 1,2,3 分别代表青年、中年和老年； A2，A3 的取值 1,2 分别代表是和否； A4 的取值 1,2,3 分别代表一般、好喝非常好； C 的取值 0,1 分别代表否和是。

---

首先在数据集 D 上计算各个特征的信息增益比，选取信息增益比最大的特征作为分支的依据。

首先计算数据集 D 的经验熵 H(D) ：
H(D)=−615log2615−915log2915=0.97095

然后计算各个特征对数据集 D 的经验条件熵 H(D|A) ：

H(D|A1)=515∗(−35log235−25log225)+515∗(−35log235−25log225)+515∗(−15log215−45log245)=0.88794

H(D|A2)=515∗(−55log255−05log205)+1015∗(−610log2610−410log2410)=0.64730

H(D|A3)=615∗(−66log266−06log206)+915∗(−39log239−69log269)=0.55098

H(D|A4)=515∗(−15log215−45log245)+615∗(−46log246−26log226)+415∗(−44log244−04log204)=0.60796

然后计算数据集 D 关于各个特征 A 的值的熵 HA(D) ：

HA1(D)HA2(D)HA3(D)HA4(D)=−515∗log2515−515∗log2515−515∗log2515=1.58496=−515∗log2515−1015∗log21015=0.91830=−615∗log2615−915∗log2915=0.97095=−515∗log2515−615∗log2615−415∗log2415=1.56605

好了，可以计算各个特征的信息增益比（ gR(D,A) ）了

gR(D,A1)gR(D,A2)gR(D,A3)gR(D,A4)=H(D)−H(D|A1)HA1(D)=0.97095−0.887941.58496=0.05237=H(D)−H(D|A1)HA1(D)=0.97095−0.647300.91830=0.35244=H(D)−H(D|A1)HA1(D)=0.97095−0.550980.97095=0.43253=H(D)−H(D|A1)HA1(D)=0.97095−0.607961.56605=0.23179

选择信息增益比最大的特征 A3 ，“有自己的房子”，作为分支的特征条件，把数据集 D 分为两部分 D1（有自己的房子）,D2（没有自己的房子） ，如下图所示：

下面分别对数据集 D1，D2 建树， D1,D2 上的特征有 A1,A2,A4 .

数据集 D1 中的实例都属于同一类（“是”），建立单节点数，类别为“是”；

分别计算针对数据集 D2 的各个特征的信息增益比。
首先计算经验熵 H(D2)

H(D2)=−39log239−69log269=0.91830

然后计算各个特征的经验条件熵 H(D2|A) ：

H(D2|A1)H(D2|A2)H(D2|A4)=49∗(−14log214−34log234)+29∗(−02log2022−22log222)+39∗(−13log213−23log223)=0.66667=39∗0+69∗0=0=49∗0+49∗(−24log224−24log224)+19∗0=0.44444

然后计算在数据集 D2 中各个特征的取值的经验熵 HA(D2) ：

HA1(D2)HA2(D2)HA4(D2)=−49log249−29log229−39log239=1.53050=−39log239−69log269=0.91830=−49log249−49log249−19log219=1.39214

下面计算各个特征的信息增益比：

gR(D2,A1)gR(D2,A2)gR(D2,A4)=H(D2)−H(D2|A1)HA1(D2)=0.91830−0.666671.53050=0.16441=H(D2)−H(D2|A2)HA2(D2)=0.91830−00.91830=1=H(D2)−H(D2|A4)HA4(D2)=0.91830−0.444441.39214=0.34038

选择信息增益比最大的特征 A2 ，有工作，作为分支的特征条件，将 D2 划分为两部分， D3:有工作，D4:没有工作 。如下图所示：

分别对数据集 D3,D4 建树，数据集的特征只有 A1,A4 ：

数据集 D3 中的所有实例都属于同一个类“是”，所以建立单节点树，类别为“是”；

同理数据集 D4 也是单节点树，类别是“否”。

建完了，树如下：

5.2 试用平方误差准则生成一个二叉回归树

输入变量是一维的，所以只要确定这个变量的一个切分点，就可以将输入空间划分为两个区域。
计算所有切分点的平方误差，取误差最小的切分点。如下图所示：

https://www.processon.com/view/link/59814675e4b02e2de77789ec

计算用python：

#!/usr/bin/env python2
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 16 01:58:43 2017

@author: zz
"""

import numpy as np

def cutPoint(arr, start, size):
    err = [0] * (size-1)
    for i in range(start+1, start+size):
        arr1 = arr[start:i]
        arr2 = arr[i:start+size]
        print i-1, ': ', (arr1.std()**2)*arr1.size, ', ', (arr2.std()**2)*arr2.size, ' mean: ', arr1.mean(), ', ', arr2.mean()
        err[i-1-start] = (arr1.std()**2)*arr1.size + (arr2.std()**2)*arr2.size

    print err
    print min(err)
    return err.index(min(err))+start

arr = np.array([4.5, 4.75, 4.91, 5.34, 5.8, 7.05, 7.9, 8.23, 8.7, 9])
start = 5
size = 5
index = cutPoint(arr, start, size)

print index, arr[index], arr[start:(index+1)].mean(), arr[(index+1):start+size].mean()

5.3 证明CART剪枝算法中，当 α 确定时，存在唯一的最小子树 Tα 使损失函数 Cα(T) 最小。

证明：
假设当 α 确定时，存在两颗子树 T1,T2 都使损失函数 Cα 最小。

可以先看 T1,T2 不同的一个分支。如下图所示， T1,T2 有相同的最小损失函数。但 T2 比较小，所以 T1 不是最小子树。

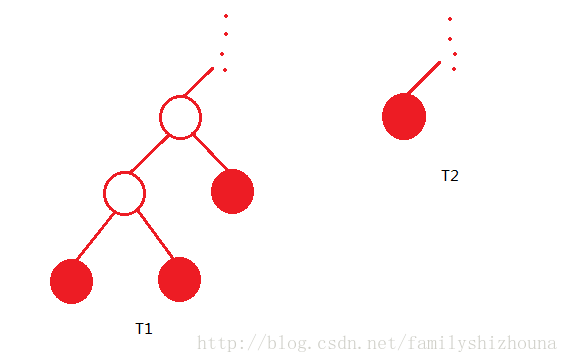
5.4 证明CART剪枝算法中求出的子树序列 {T0,T1,…,Tn} 分别是区间 α∈[αi,αi+1) 的最优子树 Tα ，这里 i=0,1,…,n,0=α0<α1<⋯<αn<+∞.

证明：
（没有证出来，未完待续。。。）
要证明 Ti 是区间 α∈[αi,αi+1) 的最优子树。

首先明确一点，损失函数 Cα(T)=C(T)+α|T| ，T是任意子树， C(T) 代表对训练数据的预测误差，树越复杂，这个值越小，树越简单，这个值越大； |T| 代表子树的叶节点个数，树越复杂，这个值越大，树越简单，这个值越小。 α 越大对应的最优子树越小， α 越小对应的最优子树越大。如下图所示：

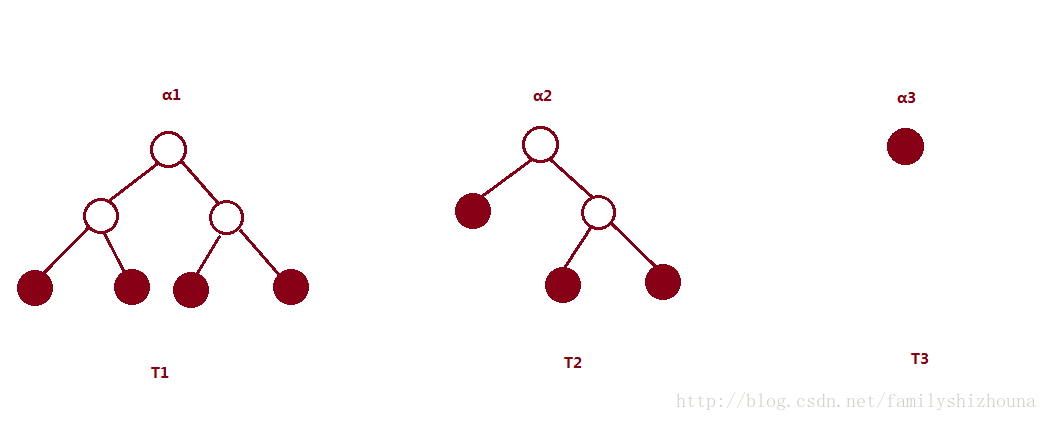
假设 T1,T2,T3 分别是参数 α1,α2,α3 对应的最优子树，有 α1≤α2≤α3

---

首先证明， α1,α2 对应的最优子树分别为 T1,T2 ，如果 |T1|>|T2| ，则 α1<α2 ；
然后证明，对内部节点 t,p ，如果节点 p 是节点 t 的祖先节点，则 g(p)>g(t) 。

首先证明， T0

---

当前的树是 Ti−1 ， αi 是这样确定的，对各内部节点 t 计算 g(t)，g(t)=C(t)−C(Tt)|Tt|−1,αi=min(g(t)) 。并对有最小 α 的节点进行剪枝，得到 Ti ， αi+1 是对树 Ti 的各内部节点计算 g(t) ，取最小的作为 αi+1 。

要证明 Ti 是区间 α∈[αi,αi+1) 的最优子树；
或者证明 Ti−1 是区间 α∈[αi−1,αi)

要证明 Ti−1 是 α∈[0,αi) 的最优子树。假设存在另一颗子树 T′i−1 是 α=α′<αi 的最优子树。这与 αi=min(g(t)) 矛盾。所以 Ti−1 是 α∈[0,αi) 的最优子树。

要证明 Ti 是 α=αi 的最优子树。假设 Ti 是减去节点 t 的子节点得到的。假设 T′i 是最优子树，如果 T′i