图像特征与描述(2)
图像特征与描述(2)
- 引言
- 1、Haar-like特征的快速计算: 积分图
- 2、局部特征: SURF
- 3、ORB特征描述
- 4、BRIEF
- 5、ORB对BRIEF的改进
- 6、其他特征提取-LBP
- 7、其他特征提取-Gabor
- 8、代码实现
- SURF
- ORB
引言
笔记总结。
1、Haar-like特征的快速计算: 积分图
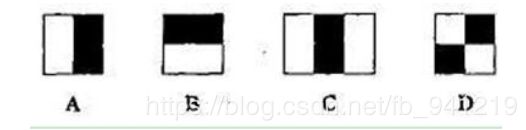
- Haar-like特征分为: 边缘特征、 线性特征、中心特征和对角线特征, 这些特征组合成特征模板。
- 特征模板内有白色和黑色两种矩形, 并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。
- Haar特征值反映了图像的灰度变化情况。
2、局部特征: SURF
- S U R F ( S p e e d e d − U p R o b u s t F e a t u r e s ) SURF(Speeded-Up Robust Features ) SURF(Speeded−UpRobustFeatures) 算子是 H e r b e r t B a y Herbert Bay HerbertBay等人在2006年提出的, 它是对SIFT的改进, 可将速度提高3倍。
- S U R F SURF SURF主要是把 S I F T SIFT SIFT中的某些运算作了简化。
- S U R F SURF SURF把 S I F T SIFT SIFT中的高斯二阶微分的模板进行了简化, 使得卷积平滑操作仅需要转换成加减运算。
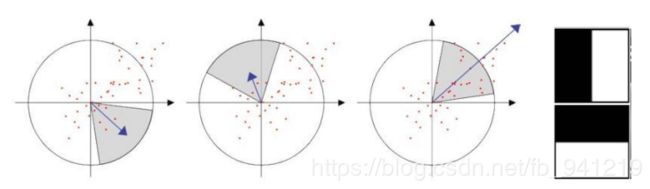
- 在方向确定阶段, 在圆形区域计算 x , y x, y x,y方向的 h a a r haar haar小波响应, 找到模最大的扇形方向。
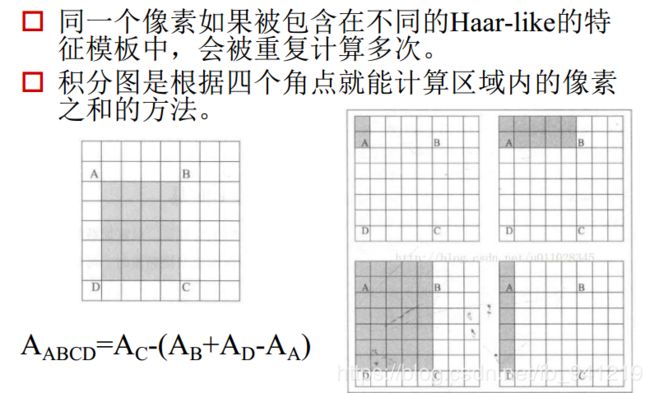
- 为了找出图像中的特征点, 需要对原图进行变换, 变换图就是原图每个像素的Hessian矩阵行列式的近似值构成的。
- 求 H e s s i a n Hessian Hessian时要先高斯平滑, 然后求二阶导数,这对于离散的像素点而言, 是用模板卷积形成的, 这两种操作合在一起用一个 H a a r Haar Haar模板代替就可以了.
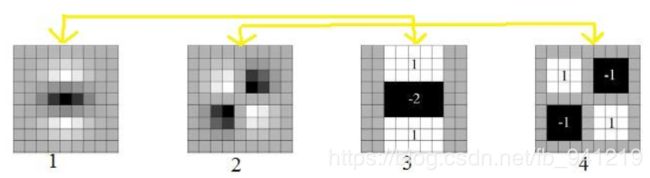
- 为了保证旋转不变性, 在SURF中, 统计特征点领域内的Haar小波特征。
- 即以特征点为中心, 计算半径为6s(s为特征点所在的尺度值)的邻域内, 统计60度扇形内所有点在x(水平)和y(垂直)方向的Haar小波响应总和。
- 然后60度扇形以一定间隔进行旋转, 最后将最大值那个扇形的方向作为该特征点的主方向。


3、ORB特征描述
SIFT与SURF计算复杂, 难以用于实时性特征检测, 更何况SIFT与SURF以前还是收费的……ORB特征基于FAST角点的特征点检测与BRIEF特征描述技术。FAST核心思想就是找出那些卓尔不群的点,即拿一个点跟它周围的点比较,如果它和其中大部分的点都不一样就可以认为它是一个特征点。

ORB的基本思路:
- 它是对FAST角点与BRIEF特征描述子的一种结合与改进。
- FAST角点检测的缺点是:
- 缺乏尺度不变性的;
- 可以通过构建高斯金字塔, 然后在每一层金字塔图像上检测角点, 来实现尺度不变性;
- BRIEF的缺点是
- 缺乏旋转不变性的;
- 需要给BRIEF加上旋转不变性。
4、BRIEF
BRIEF算法的核心思想是在关键点P的周围以一定模式选取N个点对,把这N个点对的比较结果组合起来作为描述子。 BRIEF需要先平滑图像, 然后在特征点周围选择一个Patch, 在这个Patch内通过一种选定的方法来挑选出来 n d n_d nd个点对。 比较点对中两点像素的大小, 进行如下赋值.具体来讲分为以下几步。
1.以关键点P为圆心,以d为半径做圆O。
2.在圆O内某一模式选取N个点对。这里为方便说明,N=4,实际应用中N可以取512.
假设当前选取的4个点对如上图所示分别标记为: P 1 ( A , B ) 、 P 2 ( A , B ) 、 P 3 ( A , B ) 、 P 4 ( A , B ) P_1(A,B)、 P_2(A,B)、 P_3(A,B)、 P_4(A,B) P1(A,B)、P2(A,B)、P3(A,B)、P4(A,B)3.定义操作 τ \tau τ τ ( p ; x , y ) = − { 1 if p(x)<p(y) 0 otherwise \tau (p;x,y)= -\begin{cases} 1& \text{ \quad if p(x)<p(y)}\\ 0& \text{ \quad otherwise} \end{cases} τ(p;x,y)=−{10 if p(x)
假如: τ ( P 1 ( A , B ) ) = 1 \tau(P_1(A,B)) =1 τ(P1(A,B))=1 τ ( P 2 ( A , B ) ) = 0 \tau(P_2(A,B)) =0 τ(P2(A,B))=0 τ ( P 3 ( A , B ) ) = 1 \tau(P_3(A,B)) =1 τ(P3(A,B))=1 τ ( P 4 ( A , B ) ) = 1 \tau(P_4(A,B)) =1 τ(P4(A,B))=1则最终的描述子为: 1011 1011 1011
- 所有nd个点对, 都进行比较之间, 我们就生成了一个nd长的二进制串。
- 点对的生成方式(共有5种)
- 1、 X和Y都服从在 [ − S / 2 , S / 2 ] [-S/2,S/2] [−S/2,S/2]范围内的均匀分布,且相互独立;
- 2、 X和Y都服从均值为0, 方差为 S 2 / 25 S^2/25 S2/25的高斯分 布, 且相互独立, 即 X X X和 Y Y Y都以原点为中心, 进行同方差的高斯分布;

5、ORB对BRIEF的改进
- ORB在计算BRIEF描述子时建立的坐标系是以关键点为圆心, 以关键点和取点区域的形心(圆形) 的连线为X轴建立坐标系。
- 计算形心时, 圆形区域上每个点的“质量” 是其对应的像素值。
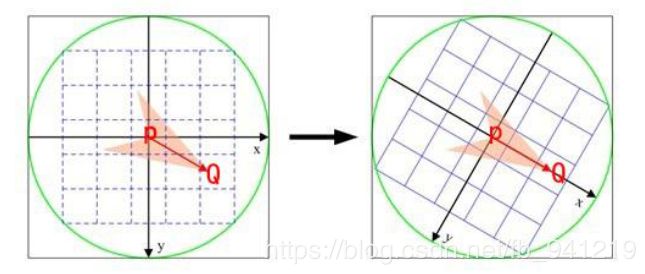
在左图中, P P P为关键点。圆内为取点区域,每个小格子代表一个像素。现在我们把这块圆心区域看做一块木板,木板上每个点的质量等于其对应的像素值。根据积分学的知识我们可以求出这个密度不均匀木板的质心 Q Q Q。计算公式如下。其中 R R R为圆的半径。 M 00 = ∑ X = − R R ∑ Y = − R R I ( x , y ) M_{00}=\sum_{X=-R }^{R}\sum_{Y=-R }^{R} I(x,y) M00=X=−R∑RY=−R∑RI(x,y)
M 10 = ∑ X = − R R ∑ Y = − R R x I ( x , y ) M_{10}=\sum_{X=-R }^{R}\sum_{Y=-R }^{R}x I(x,y) M10=X=−R∑RY=−R∑RxI(x,y)
M 01 = ∑ X = − R R ∑ Y = − R R y I ( x , y ) M_{01}=\sum_{X=-R }^{R}\sum_{Y=-R }^{R}y I(x,y) M01=X=−R∑RY=−R∑RyI(x,y)
Q x = M 10 M 00 , Q y = M 01 M 00 Q_x=\frac{M_{10}}{M_{00}}\, , \quad Q_y=\frac{M_{01}}{M_{00}} Qx=M00M10,Qy=M00M01
这里求解质心啥的当年作为考研边角知识张宇、汤家凤讲的老详细了。
圆心是固定的而且随着物体的旋转而旋转。当以 P Q PQ PQ作为坐标轴时(右图),在不同的旋转角度下,再以同一取点模式取出来的点是一致的。这就解决了旋转一致性的问题。
特征点的匹配
ORB算法最大的特点就是计算速度快 。 这首先得益于使用FAST检测特征点,FAST的检测速度正如它的名字一样是出了名的快。再次是使用BRIEF算法计算描述子,该描述子特有的2进制串的表现形式不仅节约了存储空间,而且大大缩短了匹配的时间。
例如特征点A、B的描述子如下。
A : 10101011 B : 10101010 A:10101011 \\ B:10101010 A:10101011B:10101010
设定一个阈值,比如 80 % 80\% 80%。当 A A A和 B B B的描述子的相似度大于 90 % 90\% 90%时,判断 A , B A,B A,B是相同的特征点,即这2个点匹配成功。在这个例子中 A , B A,B A,B只有最后一位不同,相似度为 87.5 % 87.5\% 87.5%,大于 80 % 80\% 80%。则 A A A和 B B B是匹配的。
将A和B进行异或操作就可以轻松计算出A和B的相似度。而异或操作可以借组硬件完成,具有很高的效率,加快了匹配的速度。
6、其他特征提取-LBP
Local Binary Pattern-LBP,LBP特征具有灰度不变性和旋转不变性等显著优点。原始的LBP算子定义在像素33的邻域内,以邻域中心像素为阈值,相邻的8个像素的灰度值与邻域中心的像素值进行比较,若周围像素大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,33邻域内的8个点经过比较可产生8位二进制数,将这8位二进制数依次排列形成一个二进制数字,这个二进制数字就是中心像素的LBP值,LBP值共有 2 8 2^8 28种可能,因此LBP值有256种。中心像素的LBP值反映了该像素周围区域的纹理信息。
备注:计算LBP特征的图像必须是灰度图,如果是彩色图,需要先转换成灰度图。
- LBP(局部二值模式)
• 将每个像素点与周围点大小比较- 半径为R的圆上, 均匀采样P个点
- 大小量化为0或1
- 多个bit组成一个数, 统计每个数的直方图
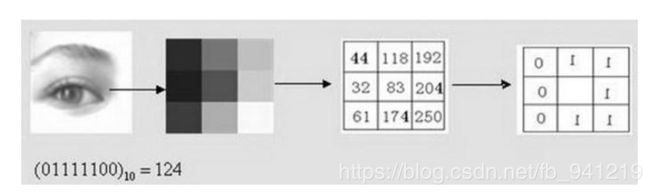
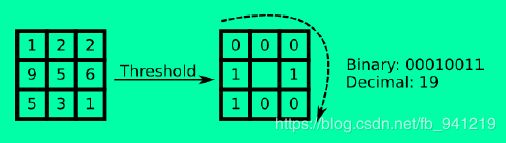
L B P ( x c , y c ) = ∑ p = 0 p − 1 2 p s ( i p − i c ) LBP(x_c,y_c)=\sum_{p=0 }^{p-1}2^ps(i_p-i_c) LBP(xc,yc)=p=0∑p−12ps(ip−ic) s ( x ) = { 0 x<0 1 else s(x)=\begin{cases} 0& \text{x<0}\\ 1& \text{else} \end{cases} s(x)={01x<0else ( x c , y c ) (xc,yc) (xc,yc)为中心像素的坐标, p p p为邻域的第 p p p个像素, i p i_p ip为邻域像素的灰度值, i c i_c ic为中心像素的灰度值, s ( x ) s(x) s(x)为符号函数.
- 为解决旋转不变性的问题; 将LBP周围的二进制码(如11110001) 按位旋转, 取二进制码最小的值为最终LBP值。
- 如: 对于 11110001 11110001 11110001情况, 我们按位旋转, 得到 11100011 , 11000111 , 10001111 , 0001111 , 00111110 , 01111100 , 11111000 11100011,11000111,10001111,0001111,00111110,01111100,11111000 11100011,11000111,10001111,0001111,00111110,01111100,11111000七个不同的二进制数, 最小值为 00011111 00011111 00011111。
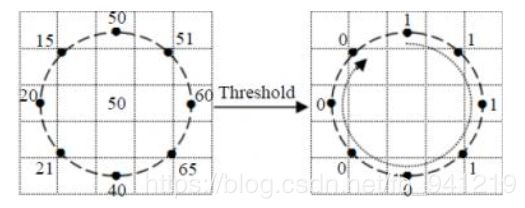
改进的LBP:
将 3×3 邻域扩展到任意邻域, 并用圆形邻域代替了正方形邻域, 这种LBP特征叫做 E x t e n d e d L B P Extended LBP ExtendedLBP, 也叫 C i r c u l a r L B P Circular LBP CircularLBP。由于原始LBP特征使用的是固定邻域内的灰度值,因此当图像的尺度发生变化时,LBP特征的编码将会发生错误,LBP特征将不能正确的反映像素点周围的纹理信息,因此研究人员对其进行了改进[3]。基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,Ojala 等对 LBP 算子进行了改进,将 3×3 邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子:
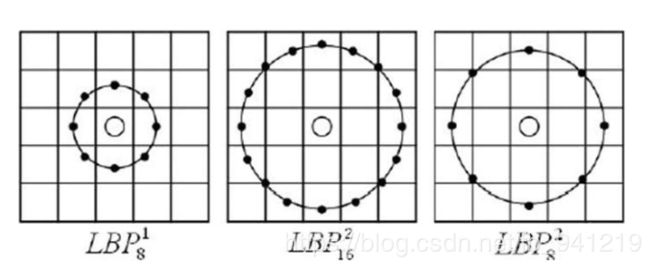
使用可变半径的圆对近邻像素进行编码 .对于给定中心点 ( x c , y c ) (xc,yc) (xc,yc),其邻域像素位置为 ( x p , y p ) , p ∈ P (xp,yp),p∈P (xp,yp),p∈P,其采样点 ( x p , y p ) (xp,yp) (xp,yp)用如下公式计算: x p = x c + R c o s ( 2 π P P ) y p = y c + R s i n ( 2 π P P ) x_p=x_c+Rcos(\frac{2\pi P}{P})\\y_p=y_c+Rsin(\frac{2\pi P}{P}) xp=xc+Rcos(P2πP)yp=yc+Rsin(P2πP) R R R是采样半径, p p p是第 p p p个采样点, P P P是采样数目。由于计算的值可能不是整数,即计算出来的点不在图像上,我们使用计算出来的点的插值点。目的的插值方法有很多,Opencv使用的是双线性插值,双线性插值的公式如下:


通过LBP特征的定义可以看出,LBP特征对光照变化是鲁棒的.
LBP及其改进参考博客
7、其他特征提取-Gabor
Gabor 特征是一种可以用来描述图像纹理信息的特征,Gabor 滤波器的频率和方向与人类的视觉系统类似,特别适合于纹理表示与判别。Gabor是一个用于边缘提取的线性滤波器, 其频率和方向表达与人类视觉系统类似, 能够提供良好的方向选择和尺度选择特性,而且对于光照变化不敏感;十分适合纹理分析;使用一个三角函数与一个高斯函数叠加就得到了一个Gabor滤波器,如图所示。
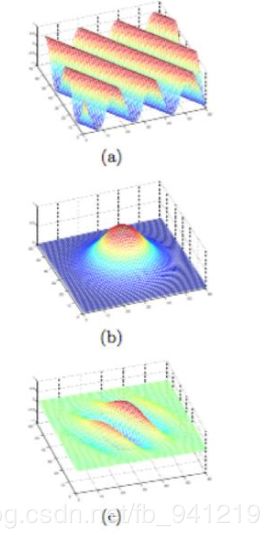
Gabor滤波器组
- Gabor 滤波器组类似于人类的视觉系统
- 多频率/尺度
- 多方向
- Gabor 滤波器
- 频域: 属于加窗傅立叶变换
- 空域: 一个高斯核函数和正弦平面波的乘积
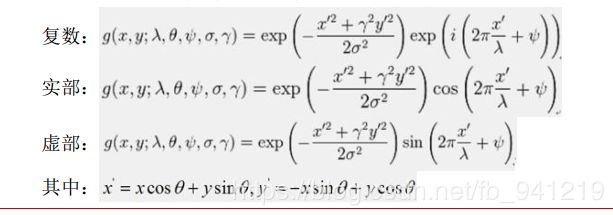
Gabor滤波器组
• 3尺度
• 8方向

8、代码实现
SURF
import numpy as np
import cv2 as cv
img = cv.imread('butterfly.jpg',0)
surf = cv.xfeatures2d.SURF_create(400)
# kp, des = surf.detectAndCompute(img,None)
surf.setHessianThreshold(50000)
kp, des = surf.detectAndCompute(img,None)
img2 = cv.drawKeypoints(img,kp,None,(255,0,0),4)
cv.imshow('surf',img2)
cv.waitKey(0)
cv.destroyAllWindows()

ORB
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
img1 = cv.imread('box.png',0) # queryImage
img2 = cv.imread('box_in_scene.png',0) # trainImage
# Initiate ORB detector
orb = cv.ORB_create()
# find the keypoints and descriptors with ORB
kp1, des1 = orb.detectAndCompute(img1,None)
kp2, des2 = orb.detectAndCompute(img2,None)
# create BFMatcher object
bf = cv.BFMatcher(cv.NORM_HAMMING, crossCheck=True)
# Match descriptors.
matches = bf.match(des1,des2)
# Sort them in the order of their distance.
matches = sorted(matches, key = lambda x:x.distance)
# Draw first 10 matches.
img3 = cv.drawMatches(img1,kp1,img2,kp2,matches[:20],None, flags=2)
plt.imshow(img3),plt.show()
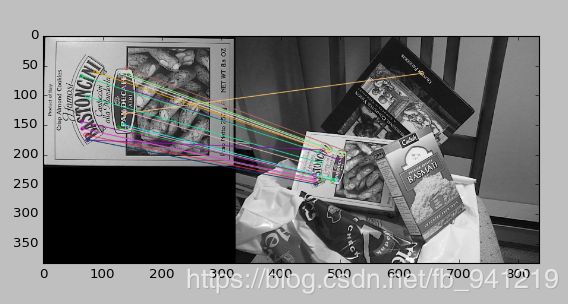
从这看,ORB的效果是真的好,速度又快,旋转一致性的解决也很明显。